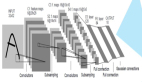
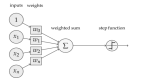
在神经网络中,激活函数决定来自给定输入集的节点的输出,其中非线性激活函数允许网络复制复杂的非线性行为。正如绝大多数神经网络借助某种形式的梯度下降进行优化,激活函数需要是可微分(或者至少是几乎完全可微分的)。此外,复杂的激活函数也许产生一些梯度消失或爆炸的问题。因此,神经网络倾向于部署若干个特定的激活函数(identity、sigmoid、ReLU 及其变体)。
下面是 26 个激活函数的图示及其一阶导数,图的右侧是一些与神经网络相关的属性。
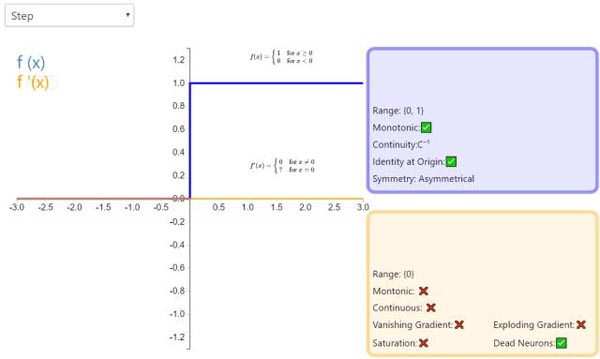
1. Step
激活函数 Step 更倾向于理论而不是实际,它模仿了生物神经元要么全有要么全无的属性。它无法应用于神经网络,因为其导数是 0(除了零点导数无定义以外),这意味着基于梯度的优化方法并不可行。
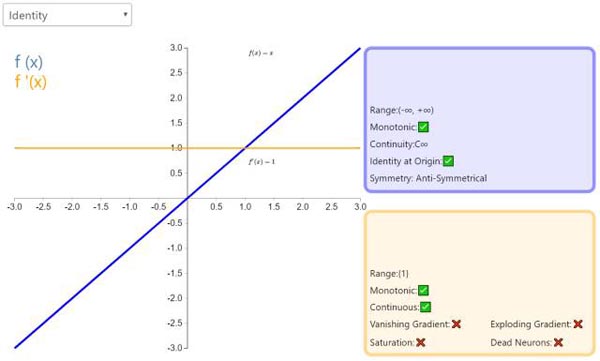
2. Identity
通过激活函数 Identity,节点的输入等于输出。它完美适合于潜在行为是线性(与线性回归相似)的任务。当存在非线性,单独使用该激活函数是不够的,但它依然可以在最终输出节点上作为激活函数用于回归任务。
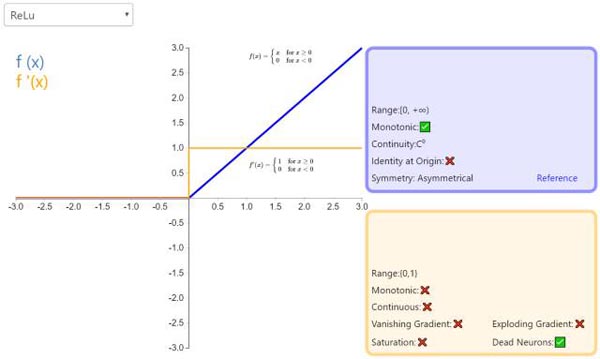
3. ReLU
修正线性单元(Rectified linear unit,ReLU)是神经网络中最常用的激活函数。它保留了 step 函数的生物学启发(只有输入超出阈值时神经元才激活),不过当输入为正的时候,导数不为零,从而允许基于梯度的学习(尽管在 x=0 的时候,导数是未定义的)。使用这个函数能使计算变得很快,因为无论是函数还是其导数都不包含复杂的数学运算。然而,当输入为负值的时候,ReLU 的学习速度可能会变得很慢,甚至使神经元直接无效,因为此时输入小于零而梯度为零,从而其权重无法得到更新,在剩下的训练过程中会一直保持静默。
4. Sigmoid
Sigmoid 因其在 logistic 回归中的重要地位而被人熟知,值域在 0 到 1 之间。Logistic Sigmoid(或者按通常的叫法,Sigmoid)激活函数给神经网络引进了概率的概念。它的导数是非零的,并且很容易计算(是其初始输出的函数)。然而,在分类任务中,sigmoid 正逐渐被 Tanh 函数取代作为标准的激活函数,因为后者为奇函数(关于原点对称)。
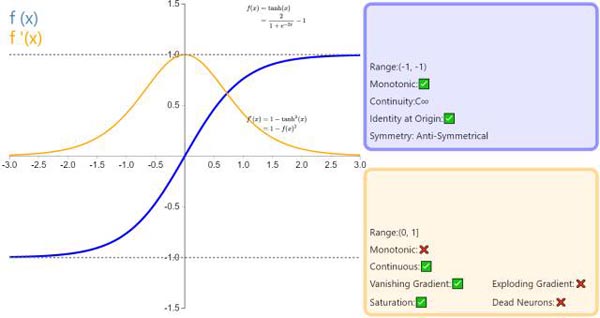
5. Tanh
在分类任务中,双曲正切函数(Tanh)逐渐取代 Sigmoid 函数作为标准的激活函数,其具有很多神经网络所钟爱的特征。它是完全可微分的,反对称,对称中心在原点。为了解决学习缓慢和/或梯度消失问题,可以使用这个函数的更加平缓的变体(log-log、softsign、symmetrical sigmoid 等等)
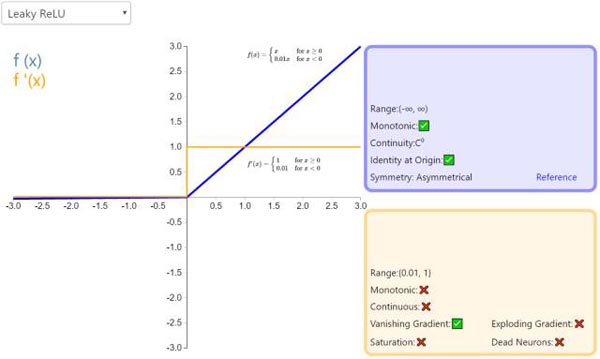
6. Leaky ReLU
经典(以及广泛使用的)ReLU 激活函数的变体,带泄露修正线性单元(Leaky ReLU)的输出对负值输入有很小的坡度。由于导数总是不为零,这能减少静默神经元的出现,允许基于梯度的学习(虽然会很慢)。
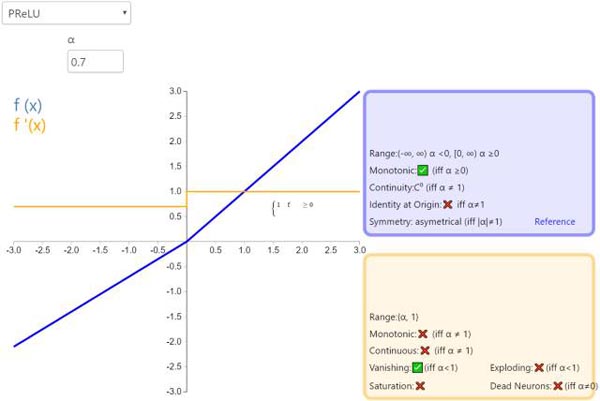
7. PReLU
参数化修正线性单元(Parameteric Rectified Linear Unit,PReLU)属于 ReLU 修正类激活函数的一员。它和 RReLU 以及 Leaky ReLU 有一些共同点,即为负值输入添加了一个线性项。而最关键的区别是,这个线性项的斜率实际上是在模型训练中学习到的。
8. RReLU
随机带泄露的修正线性单元(Randomized Leaky Rectified Linear Unit,RReLU)也属于 ReLU 修正类激活函数的一员。和 Leaky ReLU 以及 PReLU 很相似,为负值输入添加了一个线性项。而最关键的区别是,这个线性项的斜率在每一个节点上都是随机分配的(通常服从均匀分布)。
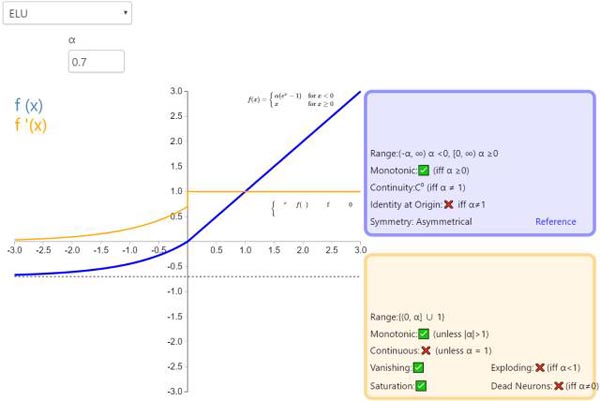
9. ELU
指数线性单元(Exponential Linear Unit,ELU)也属于 ReLU 修正类激活函数的一员。和 PReLU 以及 RReLU 类似,为负值输入添加了一个非零输出。和其它修正类激活函数不同的是,它包括一个负指数项,从而防止静默神经元出现,导数收敛为零,从而提高学习效率。
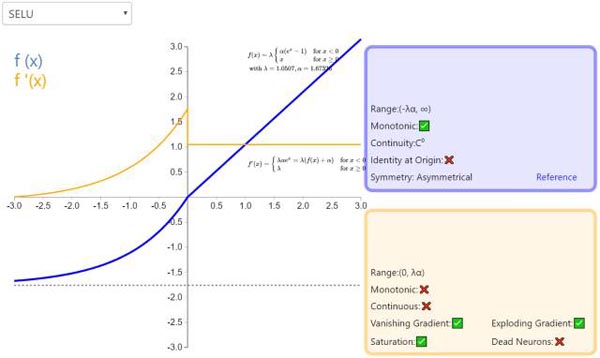
10. SELU
扩展指数线性单元(Scaled Exponential Linear Unit,SELU)是激活函数指数线性单元(ELU)的一个变种。其中λ和α是固定数值(分别为 1.0507 和 1.6726)。这些值背后的推论(零均值/单位方差)构成了自归一化神经网络的基础(SNN)。
11. SReLU
S 型整流线性激活单元(S-shaped Rectified Linear Activation Unit,SReLU)属于以 ReLU 为代表的整流激活函数族。它由三个分段线性函数组成。其中两种函数的斜度,以及函数相交的位置会在模型训练中被学习。
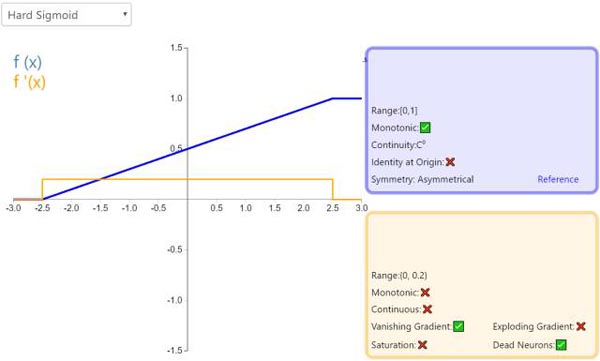
12. Hard Sigmoid
Hard Sigmoid 是 Logistic Sigmoid 激活函数的分段线性近似。它更易计算,这使得学习计算的速度更快,尽管首次派生值为零可能导致静默神经元/过慢的学习速率(详见 ReLU)。
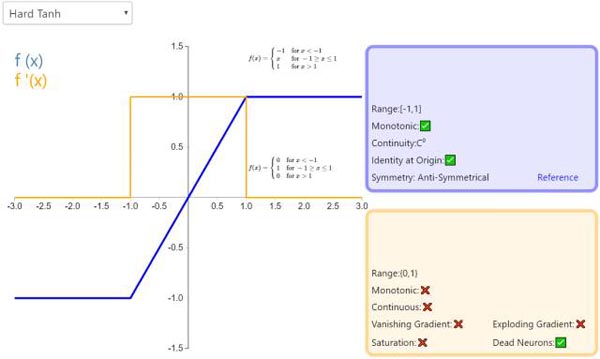
13. Hard Tanh
Hard Tanh 是 Tanh 激活函数的线性分段近似。相较而言,它更易计算,这使得学习计算的速度更快,尽管首次派生值为零可能导致静默神经元/过慢的学习速率(详见 ReLU)。
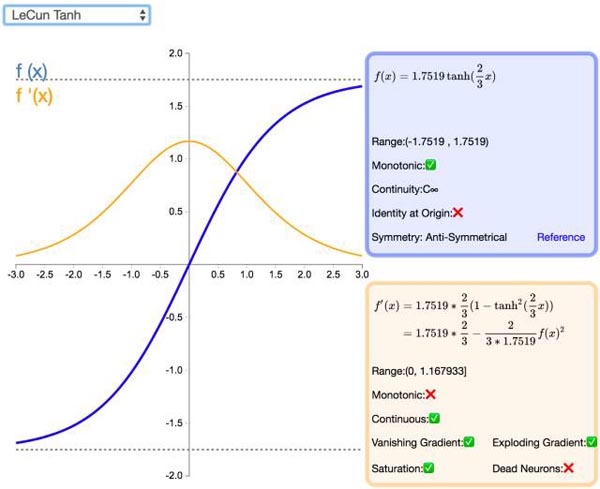
14. LeCun Tanh
LeCun Tanh(也被称作 Scaled Tanh)是 Tanh 激活函数的扩展版本。它具有以下几个可以改善学习的属性:f(± 1) = ±1;二阶导数在 x=1 最大化;且有效增益接近 1。
15. ArcTan
视觉上类似于双曲正切(Tanh)函数,ArcTan 激活函数更加平坦,这让它比其他双曲线更加清晰。在默认情况下,其输出范围在-π/2 和π/2 之间。其导数趋向于零的速度也更慢,这意味着学习的效率更高。但这也意味着,导数的计算比 Tanh 更加昂贵。
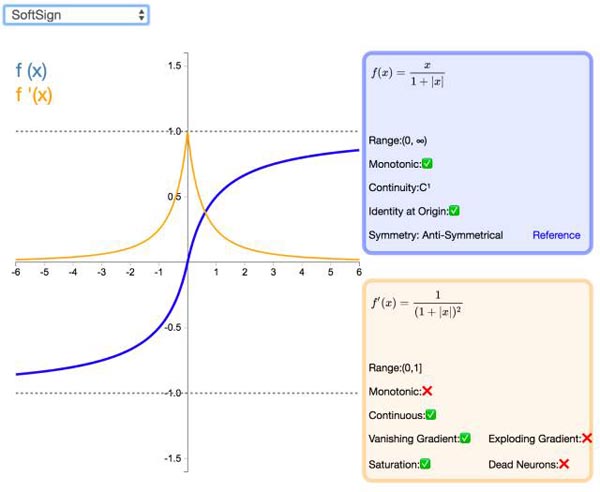
16. Softsign
Softsign 是 Tanh 激活函数的另一个替代选择。就像 Tanh 一样,Softsign 是反对称、去中心、可微分,并返回-1 和 1 之间的值。其更平坦的曲线与更慢的下降导数表明它可以更高效地学习。另一方面,导数的计算比 Tanh 更麻烦。
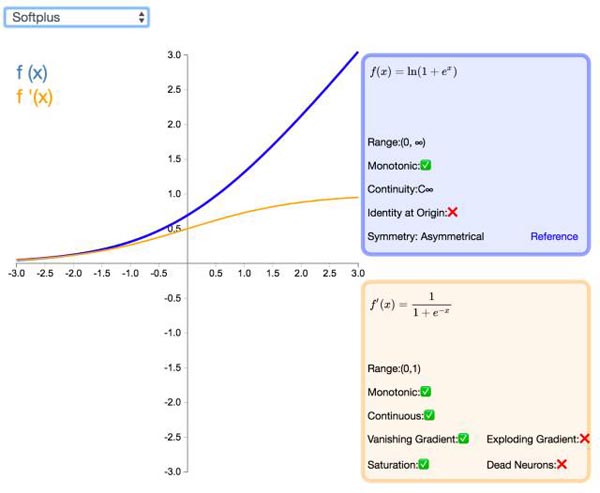
17. SoftPlus
作为 ReLU 的一个不错的替代选择,SoftPlus 能够返回任何大于 0 的值。与 ReLU 不同,SoftPlus 的导数是连续的、非零的,无处不在,从而防止出现静默神经元。然而,SoftPlus 另一个不同于 ReLU 的地方在于其不对称性,不以零为中心,这兴许会妨碍学习。此外,由于导数常常小于 1,也可能出现梯度消失的问题。
18. Signum
激活函数 Signum(或者简写为 Sign)是二值阶跃激活函数的扩展版本。它的值域为 [-1,1],原点值是 0。尽管缺少阶跃函数的生物动机,Signum 依然是反对称的,这对激活函数来说是一个有利的特征。
19. Bent Identity
激活函数 Bent Identity 是介于 Identity 与 ReLU 之间的一种折衷选择。它允许非线性行为,尽管其非零导数有效提升了学习并克服了与 ReLU 相关的静默神经元的问题。由于其导数可在 1 的任意一侧返回值,因此它可能容易受到梯度爆炸和消失的影响。
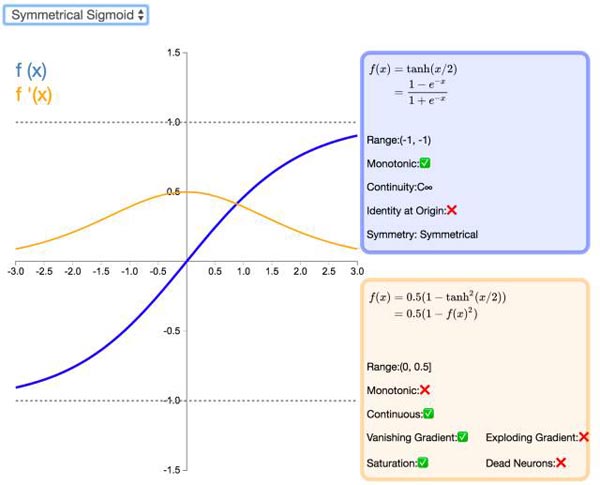
20. Symmetrical Sigmoid
Symmetrical Sigmoid 是另一个 Tanh 激活函数的变种(实际上,它相当于输入减半的 Tanh)。和 Tanh 一样,它是反对称的、零中心、可微分的,值域在 -1 到 1 之间。它更平坦的形状和更慢的下降派生表明它可以更有效地进行学习。
21. Log Log
Log Log 激活函数(由上图 f(x) 可知该函数为以 e 为底的嵌套指数函数)的值域为 [0,1],Complementary Log Log 激活函数有潜力替代经典的 Sigmoid 激活函数。该函数饱和地更快,且零点值要高于 0.5。
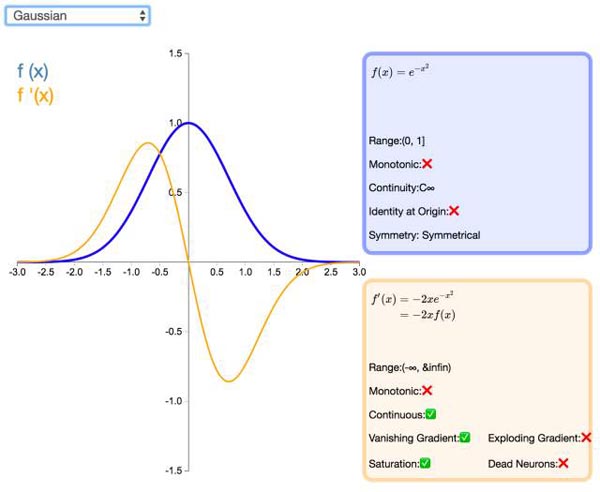
22. Gaussian
高斯激活函数(Gaussian)并不是径向基函数网络(RBFN)中常用的高斯核函数,高斯激活函数在多层感知机类的模型中并不是很流行。该函数处处可微且为偶函数,但一阶导会很快收敛到零。
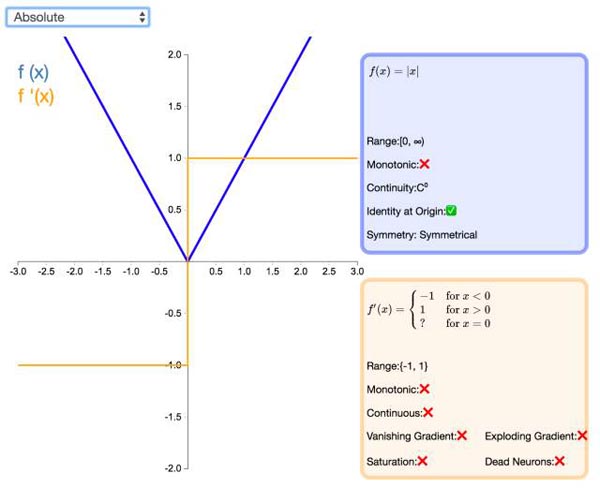
23. Absolute
顾名思义,绝对值(Absolute)激活函数返回输入的绝对值。该函数的导数除了零点外处处有定义,且导数的量值处处为 1。这种激活函数一定不会出现梯度爆炸或消失的情况。
24. Sinusoid
如同余弦函数,Sinusoid(或简单正弦函数)激活函数为神经网络引入了周期性。该函数的值域为 [-1,1],且导数处处连续。此外,Sinusoid 激活函数为零点对称的奇函数。
25. Cos
如同正弦函数,余弦激活函数(Cos/Cosine)为神经网络引入了周期性。它的值域为 [-1,1],且导数处处连续。和 Sinusoid 函数不同,余弦函数为不以零点对称的偶函数。
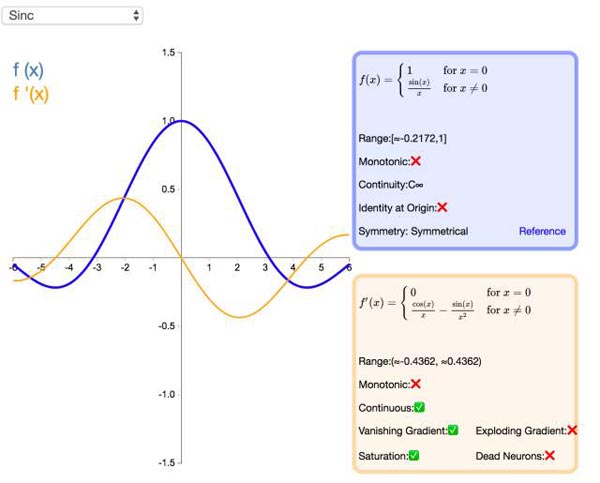
26. Sinc
Sinc 函数(全称是 Cardinal Sine)在信号处理中尤为重要,因为它表征了矩形函数的傅立叶变换(Fourier transform)。作为一种激活函数,它的优势在于处处可微和对称的特性,不过它比较容易产生梯度消失的问题。