深度学习是一个高度迭代的过程。必须尝试超参数的各种排列才能确定最佳组合。因此,在不影响成本的前提下,深度学习模式必须在更短的时间内进行训练。本文将解释深度学习中常用优化算法背后的数学原理。
优化算法
在算法f(x)中,优化算法可得到f(x)的最大值或最小值。在深度学习中,可通过优化代价函数J来训练神经网络。代价函数为:
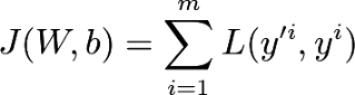
代价函数J的值是预测值y '与实际值y之间损失L的均值。利用网络的权值W和偏置b,在正向传播过程中得到y '值。通过优化算法更新可训练参数W和b的值,从而使代价函数J的值最小化。
梯度下降法
权值矩阵W是随机初始化的。利用梯度下降法可使代价函数J最小化,得到最优权矩阵W和偏置b。梯度下降法是一种求函数最小值的一阶迭代优化算法。将代价函数J应用于梯度下降法来最小化成本。数学上可定义为:
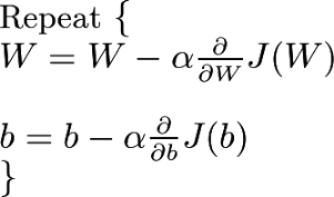
第一个方程表示权值矩阵W的变化量,第二个方程表示偏置b的变化量。这两个值的变化由学习率和成本J对权值矩阵W和偏置b的导数决定。反复更新W和 b,直到代价函数J最小化。接下来本文将通过下图来解释梯度下降法的原理:
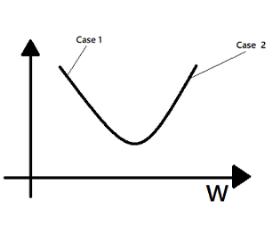
- 案例1. 假设W初始值小于其达到全局最小值时的值。这一点的斜率J对W的偏导数为负,因此,根据梯度下降方程,权值增加。
- 案例2. 假设W初始值大于其达到全局最小值时的值。这一点的斜率J对W的偏导数为正,因此,根据梯度下降方程权值下降。
因此,W和b都取得最优值,代价函数J的值被最小化。

以上给出了以梯度下降法为优化算法的基本策略。
小批量梯度下降法
梯度下降法的缺点之一是只有在经过完整的训练数据后才可更新参数。当训练数据过大无法载入计算机内存时,这无疑构成了一大挑战。小批量梯度下降法是解决上述梯度下降问题的一种应变之法。
在小批量梯度下降中,可根据用例将整个训练数据分布在大小为16、32、64等的小批量中。然后使用这些小批量来迭代训练网络。使用小批量有以下两个优点:
- 在最初的几个训练案例中,只要遍历第一个小批量,即可开始训练。
- 当拥有大量不适合储入内存的数据时,可以训练一个神经网络。
现在batch_size成为新的模型超参数。
- 当batch_size = number of training examples (训练样本数)时,称为批量梯度下降。此时就存在着需要遍历整个数据集后才能开始学习的问题。
- 当batch_size = 1时,称为随机梯度下降。由于没有充分利用矢量化,训练将变得非常缓慢。
- 因此,通常选择64或128或256或512。然而,这取决于用例和系统内存,换而言之,应确保一个小批量能载入系统内存。

以上给出了采用小批量梯度下降法作为优化算法的基本策略。
Momentum
动量梯度下降法是一种先进的优化算法,可加快代价函数J的优化。动量梯度下降法利用移动平均来更新神经网络的可训练参数。
移动平均值是在n个连续值上计算的平均值,而不是整组值。数学上表示为:
这里,A[i]表示X[i]值在i数据点处的移动平均值。参数β决定计算平均值的数值n。例如,如果β= 0.9,移动平均值用10个连续值来计算;如果β= 0.99, 移动平均值用100个连续值来计算。一般情况下,n的值可近似为:
下图显示了移动平均线的工作原理。随着β值增加,n增加,图形偏向右边,这是因为初始阶段,这些值都会增加。然而,当β减少,n减少,就可以正确建模X。因此有必要找出适当的β值以得到良好的移动平均线。可以看出β= 0.9时适用于大多数情况。
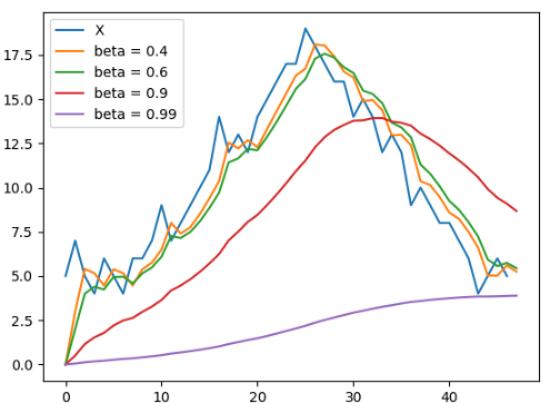
现在,了解了什么是移动平均线,接下来试着理解其在动量算法中的应用。训练神经网络时,目标是优化代价函数J,使其值最小化。传统梯度下降优化器遵循蓝色路径,而动量优化器遵循绿色路径以达到最小值(红色)。
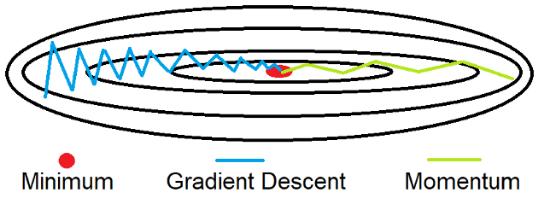
与动量相比,梯度下降的路径步骤过多。这是因为梯度下降在y轴上有很大波动,而在x轴上移动得很少,也就接近最小值。正确的解决方案是通过抑制y轴的运动来减少波动。这就是移动平均线发挥作用的地方。
观察蓝色的路径,可以看到y轴上的运动是一系列的正负变化。将加权平均应用于几乎为零的运动,随后即出现y轴上的波动。对于x轴的运动也有类似的直觉。这减少了路径上的波动,最终,随着训练迭代次数的减少,神经网络在较短的时间内达到最小值。为此,引入两个新的变量VdW和Vdb来跟踪权值dW和偏置db的导数的加权平均值。
值得注意的是,由于只有参数更新方法发生了更改,所以也可使用小批量处理方法和力矩优化器。

以上给出了以动量为优化算法的基本策略。
RMS Prop
RMS Prop是指均方根传播,与动量类似,它是一种抑制y轴运动的技术。前面的示例有助于理解其原理。为了更好地理解,这里将y轴表示为偏置b,把x轴表示为权重W。
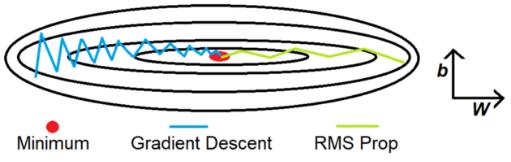
凭直觉而言,当用一个大数除以另一个数时,结果会变得很小。该例中,第一个大数为db,第二大数为加权平均db²。引入了两个新的变量Sdb和SdW,跟踪db²和dW²的加权平均。db和Sdb相除得到一个更小的值,它抑制了y轴的运动。引入Ⲉ避免出现除以零的错误。对于 x轴上W的值的更新也有类似的直觉。
值得注意的是,这里以y轴为偏置b, x轴为权值W,以便更好地理解和可视化参数的更新。也可用类似的方法消除由任何偏置b(b1, b2,…,bn)或权值W(W1, W2,…,Wn)或两者引起的任何波动。同样,由于只有参数更新方法发生了更改,也可使用小批量处理方法和均方根优化器(RMS optimizer)。

以上给出了使用RMS Prop作为优化算法时的基本策略。
AdaM
AdaM是指适应性动量。它使用单一方法结合动量和RMS prop,是一种强大而快速的优化器。也可利用误差修正方法解决加权平均计算中的冷启动问题(即加权平均值的前几个值与实际值相差太远)。V值包含动量逻辑,而S值包含RMS prop逻辑。
值得注意的是,计算中使用2个不同的β值。β1用于计算相关动量,而β2用于计算相关RMS prop。同样,由于只有参数更新方法发生了更改,所以也可使用小批量处理方法和AdaM 优化器。

以上给出了使用AdaM作为优化算法时的基本策略。
性能比较
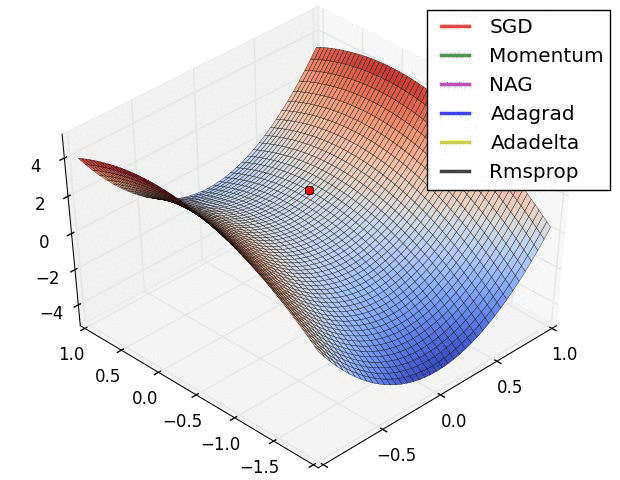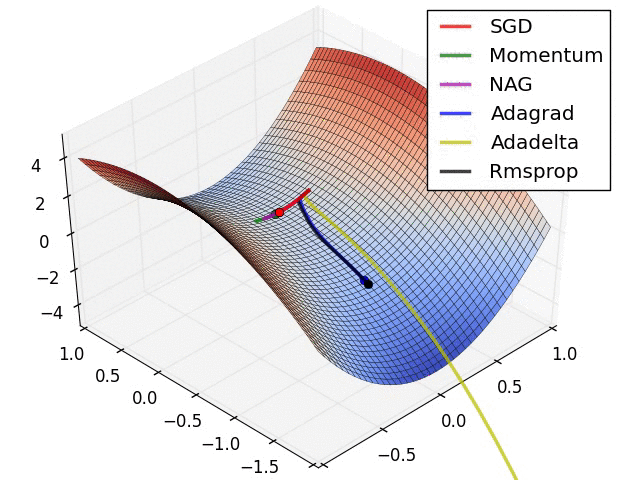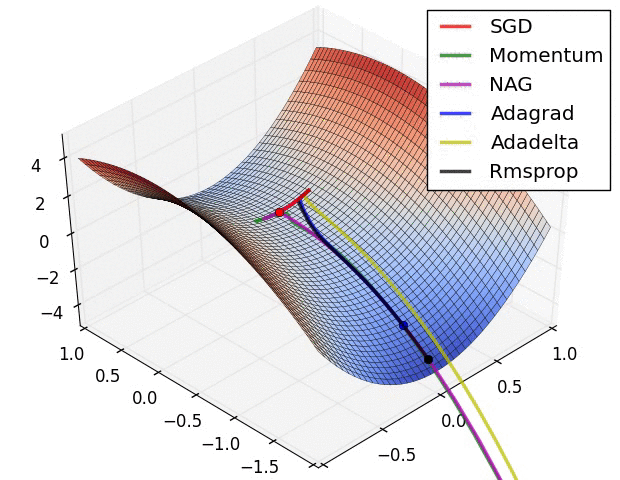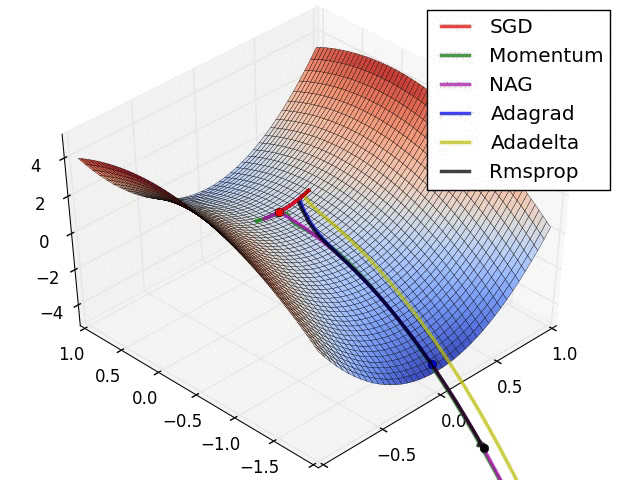
图1
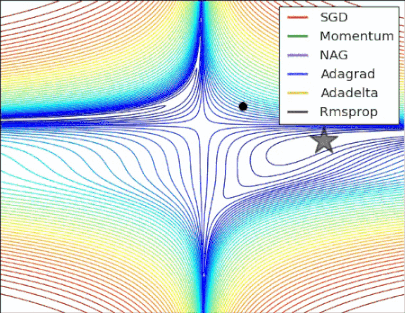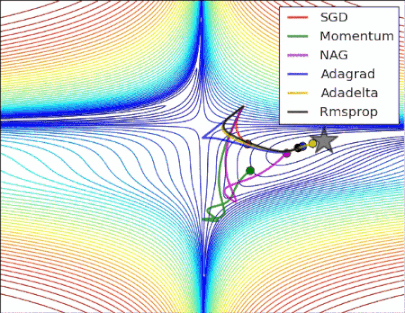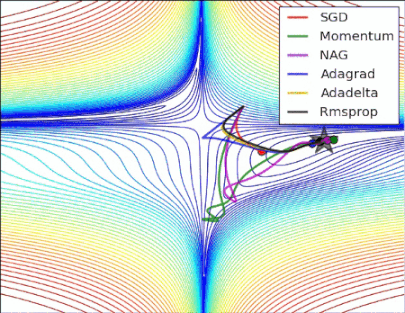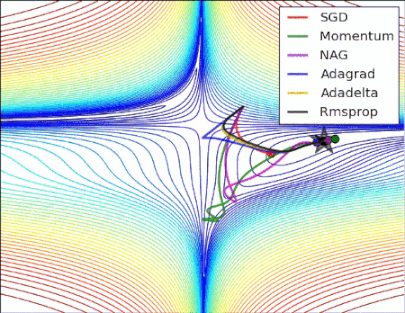
图2
损失曲面的轮廓及不同优化算法的时间演化