01
准备数据集
采用的数据集是sklearn中的breast cancer数据集,30维特征,569个样本。训练前进行MinMax标准化缩放至[0,1]区间。按照75/25比例划分成训练集和验证集。
# 获取数据集
import numpy as np
import pandas as pd
from sklearn import datasets
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
breast = datasets.load_breast_cancer()
scaler = preprocessing.MinMaxScaler()
data = scaler.fit_transform(breast['data'])
target = breast['target']
X_train,X_test,y_train,y_test = train_test_split(data,target)
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
02
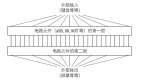
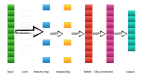
模型结构图
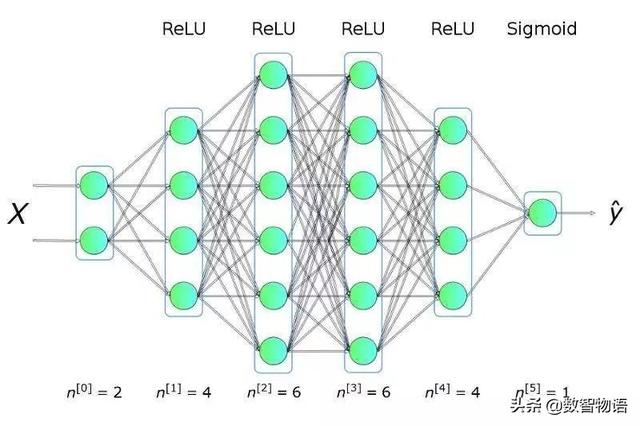
03
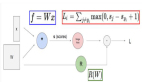
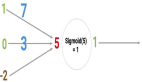
正反传播公式
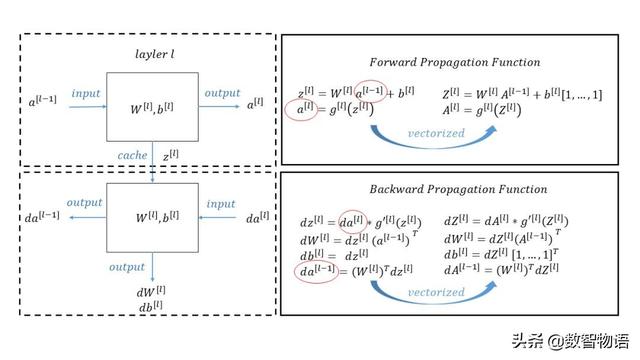
04
NN实现代码
import numpy as np
import pandas as pd
#定义激活函数
ReLu = lambda z:np.maximum(0.0,z)
d_ReLu = lambda z:np.where(z<0,0,1)
LeakyReLu = lambda z:np.maximum(0.01*z,z)
d_LeakyReLu = lambda z:np.where(z<0,0.01,1)
Sigmoid = lambda z:1/(1+np.exp(-z))
d_Sigmoid = lambda z: Sigmoid(z)*(1-Sigmoid(z)) #d_Sigmoid = a(1-a)
Tanh = np.tanh
d_Tanh = lambda z:1 - Tanh(z)**2 #d_Tanh = 1 - a**2
class NNClassifier(object):
def __init__(self,n = [np.nan,5,5,1],alpha = 0.1,ITERNUM = 50000, gfunc = 'ReLu'):
self.n = n #各层节点数
self.gfunc = gfunc #隐藏层激活函数
self.alpha,self.ITERNUM = alpha,ITERNUM
self.dfJ = pd.DataFrame(data = np.zeros((ITERNUM,1)),columns = ['J'])
self.W,self.b = np.nan,np.nan
# 确定各层激活函数
self.g = [eval(self.gfunc) for i in range(len(n))];
self.g[-1] = Sigmoid;self.g[0] = np.nan
# 确定隐藏层激活函数的导数
self.d_gfunc = eval('d_' + self.gfunc)
def fit(self,X_train,y_train):
X,Y = X_train.T,y_train.reshape(1,-1)
m = X.shape[1] #样本个数
n = self.n; n[0] = X.shape[0] # 各层节点数量
# 节点值和参数初始化
A = [np.zeros((ni,m)) for ni in n];A[0] = X #各层节点输出值初始化
Z = [np.zeros((ni,m)) for ni in n];Z[0] = np.nan #各层节点中间值初始化
W = [np.nan] + [np.random.randn(n[i],n[i-1]) * 0.01 for i in range(1,len(n))] #各层系数参数
b = [np.zeros((ni,1)) for ni in n];b[0] = np.nan #n各层偏置参数
# 导数初始化
dA = [np.zeros(Ai.shape) for Ai in A]
dZ = [np.zeros(Ai.shape) for Ai in A]
dW = [np.zeros(Wi.shape) if isinstance(Wi,np.ndarray) else np.nan for Wi in W]
db = [np.zeros(bi.shape) if isinstance(bi,np.ndarray) else np.nan for bi in b]
for k in range(self.ITERNUM):
# ---------正向传播 ----------
for i in range(1,len(n)):
Z[i] = np.dot(W[i],A[i-1]) + b[i]
A[i] = self.g[i](Z[i])
J = (1/m) * np.sum(- Y*np.log(A[len(n)-1]) -(1-Y)*np.log(1-A[len(n)-1]))
self.dfJ.loc[k]['J']= J
# ----------反向传播 ---------
hmax = len(n) - 1
dA[hmax] = 1/m*(-Y/A[hmax] + (1-Y)/(1-A[hmax]))
dZ[hmax] = 1/m*(A[hmax]-Y)
dW[hmax] = np.dot(dZ[hmax],A[hmax-1].T)
db[hmax] = np.dot(dZ[hmax],np.ones((m,1)))
for i in range(len(n)-2,0,-1):
dA[i] = np.dot(W[i+1].T,dZ[i+1])
dZ[i] = dA[i]* self.d_gfunc(Z[i])
dW[i] = np.dot(dZ[i],A[i-1].T)
db[i] = np.dot(dZ[i],np.ones((m,1)))
#-----------梯度下降 ---------
for i in range(1,len(n)):
W[i] = W[i] - self.alpha*dW[i]
b[i] = b[i] - self.alpha*db[i]
# 显示进度
if (k+1)%1000 == 0:
print('progress rate:{}/{}'.format(k+1,self.ITERNUM),end = '\r')
self.W,self.b = W,b
def predict_prob(self,X_test):
# ---------正向传播 ----------
W,b = self.W,self.b
Ai = X_test.T
for i in range(1,len(self.n)):
Zi = np.dot(W[i],Ai) + b[i]
Ai = self.g[i](Zi)
return(Ai.reshape(-1))
def predict(self,X_test):
Y_prob = self.predict_prob(X_test)
Y_test = Y_prob.copy()
Y_test[Y_prob>=0.5] = 1
Y_test[Y_prob< 0.5] = 0
return(Y_test)
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
- 54.
- 55.
- 56.
- 57.
- 58.
- 59.
- 60.
- 61.
- 62.
- 63.
- 64.
- 65.
- 66.
- 67.
- 68.
- 69.
- 70.
- 71.
- 72.
- 73.
- 74.
- 75.
- 76.
- 77.
05
单隐层神经网络
设置1个隐藏层,隐藏层节点数为5,隐藏层使用Sigmoid激活函数。
# 采用Sigmoid激活函数
NN = NNClassifier(n = [np.nan,5,1],alpha = 0.02,
ITERNUM = 200000, gfunc = 'Sigmoid')
NN.fit(X_train,y_train)
# 绘制目标函数迭代曲线
%matplotlib inline
NN.dfJ.plot(figsize = (12,8))
# 测试在验证集的auc得分
from sklearn.metrics import roc_auc_score
Y_prob = NN.predict_prob(X_test)
roc_auc_score(list(y_test),list(Y_prob))
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
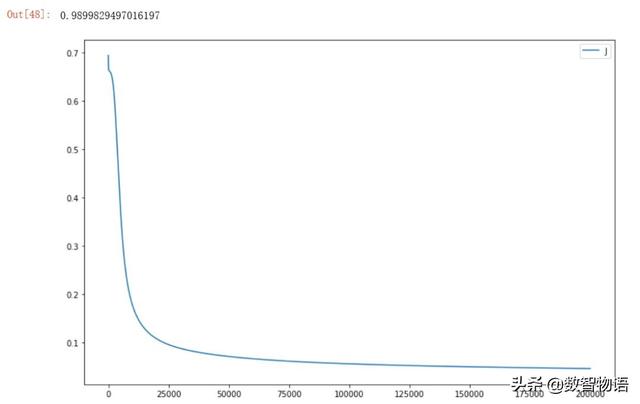
隐藏层使用Tanh激活函数。
# 采用 Tanh激活函数
NN = NNClassifier(n = [np.nan,5,1],alpha = 0.02,
ITERNUM = 200000, gfunc = 'Tanh')
NN.fit(X_train,y_train)
# 绘制目标函数迭代曲线
%matplotlib inline
NN.dfJ.plot(figsize = (12,8))
# 测试在验证集的auc得分
from sklearn.metrics import roc_auc_score
Y_prob = NN.predict_prob(X_test)
roc_auc_score(list(y_test),list(Y_prob))
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
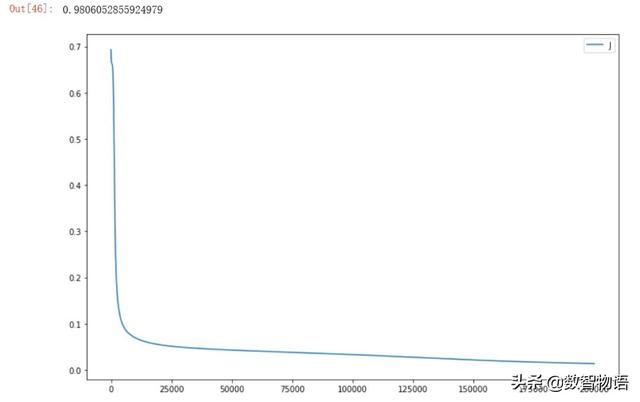
隐藏层使用ReLu激活函数。
# 采用 ReLu激活函数
NN = NNClassifier(n = [np.nan,5,1],alpha = 0.02,
ITERNUM = 200000, gfunc = 'ReLu')
NN.fit(X_train,y_train)
# 绘制目标函数迭代曲线
%matplotlib inline
NN.dfJ.plot(figsize = (12,8))
# 测试在验证集的auc得分
from sklearn.metrics import roc_auc_score
Y_prob = NN.predict_prob(X_test)
roc_auc_score(list(y_test),list(Y_prob))
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
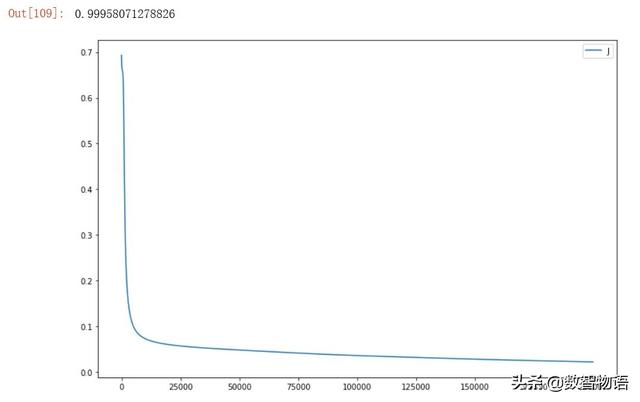
隐藏层使用LeakyReLu激活函数。
# 采用 LeakyReLu激活函数
NN = NNClassifier(n = [np.nan,5,1],alpha = 0.02,
ITERNUM = 200000, gfunc = 'LeakyReLu')
NN.fit(X_train,y_train)
# 绘制目标函数迭代曲线
%matplotlib inline
NN.dfJ.plot(figsize = (12,8))
# 测试在验证集的auc得分
from sklearn.metrics import roc_auc_score
Y_prob = NN.predict_prob(X_test)
roc_auc_score(list(y_test),list(Y_prob))
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
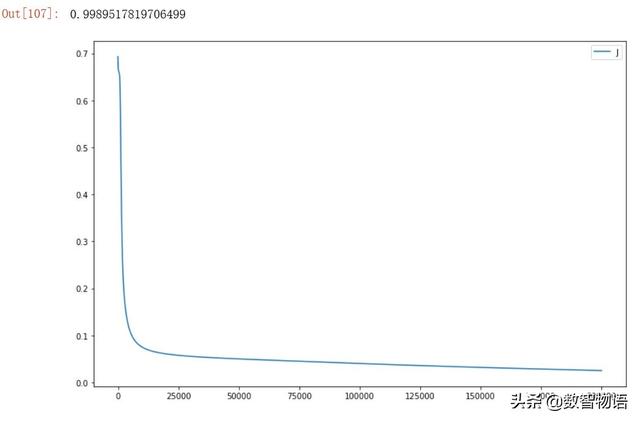
以上试验似乎表明,在当前的数据集上,隐藏层采用ReLu激活函数是一个最好的选择,AUC最高得分为0.99958。
06
双隐层神经网络
设置2个隐藏层,隐藏层节点数都为5,隐藏层都使用ReLu激活函数。
# 设置两个隐藏层,采用ReLu激活函数
NN = NNClassifier(n = [np.nan,5,5,1],alpha = 0.02,
ITERNUM = 200000, gfunc = 'ReLu')
NN.fit(X_train,y_train)
# 绘制目标函数迭代曲线
%matplotlib inline
NN.dfJ.plot(figsize = (12,8))
# 测试在验证集的auc得分
from sklearn.metrics import roc_auc_score
Y_prob = NN.predict_prob(X_test)
roc_auc_score(list(y_test),list(Y_prob))
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
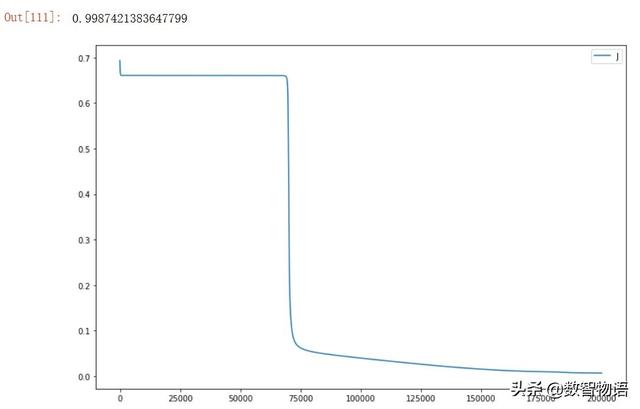
AUC得分0.99874比采用单隐藏层的最优得分0.99958有所降低,可能是模型复杂度过高,我们尝试减少隐藏层节点的个数至3以降低模型复杂度。
# 双隐藏层,隐藏层节点数为3
NN = NNClassifier(n = [np.nan,3,3,1],alpha = 0.02,
ITERNUM = 200000, gfunc = 'ReLu')
NN.fit(X_train,y_train)
# 绘制目标函数迭代曲线
%matplotlib inline
NN.dfJ.plot(figsize = (12,8))
# 测试在验证集的auc得分
from sklearn.metrics import roc_auc_score
Y_prob = NN.predict_prob(X_test)
roc_auc_score(list(y_test),list(Y_prob))
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
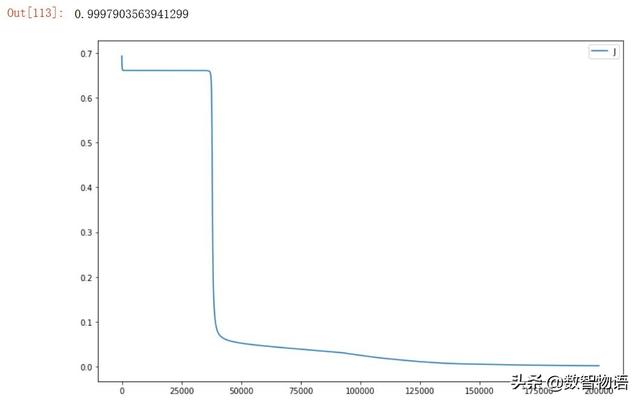
AUC得分0.99979,又有所提高。
和sklearn中自带的神经网络分类器进行对比。
# 和sklearn中的模型对比
from sklearn.neural_network import MLPClassifier
# 第一隐藏层神经元个数为3,第二隐藏层神经元个数为3
MLPClf = MLPClassifier(hidden_layer_sizes=(3,3),max_iter=200000,activation='relu')
MLPClf.fit(X_train,y_train)
# 绘制目标函数迭代曲线
dfJ = pd.DataFrame(data = np.array(MLPClf.loss_curve_),columns = ['J'])
dfJ.plot(figsize = (12,8))
# 测试在验证集的auc得分
from sklearn.metrics import roc_auc_score
Y_prob = MLPClf.predict_proba(X_test)[:,1]
roc_auc_score(list(y_test),list(Y_prob))
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
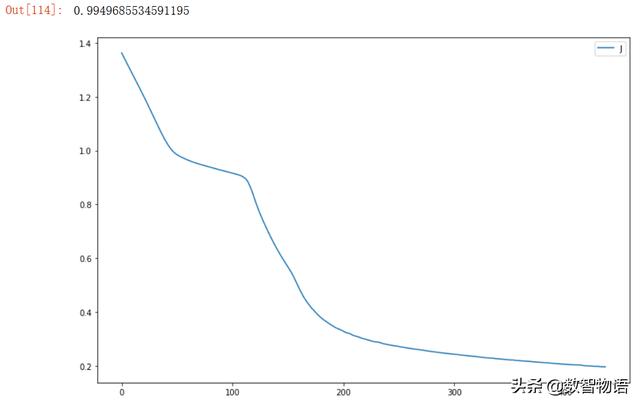
以上试验表明,针对当前数据数据集,选择ReLu激活函数,采用双隐藏层,每个隐藏层节点数设置为3是一个不错的选择,AUC得分为0.99979。该得分高于采用CV交叉验证优化超参数后的逻辑回归模型的0.99897的AUC得分。