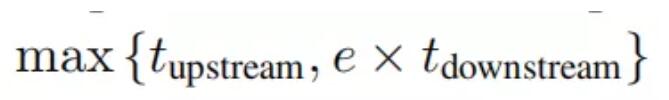在摩尔定律的暮色中,GPU 和其他硬件加速器极大地加速了神经网络的训练。但是,训练过程的前期阶段(如磁盘读写和数据预处理)并不在加速器上运行。随着加速器的不断改进,这些前期阶段所花费的时间将逐渐成为训练速度的瓶颈。谷歌大脑团队提出了“数据回送(data echoing)”算法,它减少了训练前期阶段的总计算量,并在加速器上游的计算占用训练时间时加快训练速度。“数据回送”复用训练前期阶段的中间输出,以利用闲置的计算空间。作者研究了在不同任务、不同数量的回送以及不同批尺寸时数据回送算法的表现。在所有的情况下,至少有一种数据回送算法可以用更少的上游计算达到模型的基线性能。在部分情况下,数据回送甚至可以将训练速度提升 4 倍。
1、引言
在过去的十年中,神经网络的训练速度得到了极大的提升。研究人员能够使用更大的数据集训练更大的模型,并更快地探索新的想法,显著提高了模型的表现性能。随着摩尔定律的失效,通用处理器的速度已经不能满足要求,但特定的加速器通过优化特定操作得到显著的加速。例如,GPU 和 TPU 优化了高度并行的矩阵运算,而矩阵运算正是神经网络训练算法的核心组成部分。
然而,训练一个神经网络需要的不仅仅是在加速器上运行的操作。训练程序需要读取和解压缩训练数据,对其进行打乱(shuffle)、批处理,甚至转换或增强操作。这些步骤需要用到多个系统组件,包括 CPU、磁盘、网络带宽和内存带宽。这些通用操作涉及的组件太多,为它们设计专用的加速硬件是不切实际的。同时,加速器的改进远远超过了通用计算的改进,并且在加速器上运行的代码只占用整个训练时间的一小部分。因此,如果想使神经网络训练地更快,有以下两个方法:(1)使非加速器工作地更快,或(2)减少非加速器所需的工作量。选项(1)可能需要大量的工程工作或技术探索,给系统增加太多的复杂性。因此,作者将重点放在选项(2)上,探索减少训练前期阶段的工作量的方法。
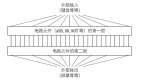
神经网络的训练过程可以看作是一个数据流程,需要对计算进行缓冲和重叠。例如,图 1 显示了小批次随机梯度下降(SGD)及其变体的典型训练流程,这是训练神经网络的标准算法。训练程序首先读取和解码输入数据,然后对数据进行 shuffle,应用一组转换操作来增加数据,并将数据分成不同批次。最后,通过迭代更新网络参数降低损失函数值;此阶段称为“SGD 更新”。由于任何流程阶段的输出都可以缓冲,因此不同阶段的计算互相重叠,最慢的阶段将占用主要的训练时间。
图 1 经典神经网络训练流程图
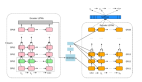
图 2 数据回送插入点的上游和下游的覆盖计算时间
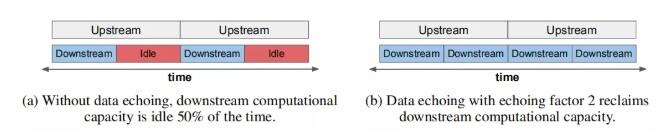
在这篇论文中,作者研究如何通过减少训练前期部分的时间来加速神经网络训练(图 2a)。作者将训练过程中第一部分的输出重复用于多个 SGD 更新,以利用空闲计算能力。这类算法称为 “数据回送”(data echoing),每个中间输出被使用的次数称为 回送因子(echoing factor)。
数据回送算法在训练流程中的某个位置(SGD 更新之前)插入重复阶段。如果上游任务(重复阶段之前)花费的时间超过下游任务(重复阶段之后)花费的时间,算法将回收下游闲置的计算能力,并提高模型的 SGD 更新率(图 2b)。通过改变插入点、回送因子和 shuffle 程度,可以得到不同的数据回送算法。
要点
- 在不同的数据集和模型结构上,数据回送在取得竞争性表现的同时减少了上游计算量;
- 支持大范围的回送因子;
- 有效性取决于训练流程中的插入点;
- 数据回送可以从回送后的 shuffle 中获益;
- 数据回送与调优的基线模型取得相同的错误率。
2 、数据回送
其中 tupstream 是回送上游所有阶段所用的时间,tdownstream 是回送下游所有阶段所用的时间,e 是回送因子。假设 tupstream≥tdownstream,这是使用数据回送的主要动机。如果用 R=tupstream/tdownstream 表示上下游处理时间之比,那么完成一个上游步骤和 e 个下游步骤的时间对于从 e 到 R 的所有回送因子都是相同的。换句话说,额外的下游步骤是“无消耗的”,因为它们使用的是空闲的下游计算能力。
使用数据回送时,减少的训练时间取决于上游步骤和下游步骤之间的比重。一方面,由于重复数据的价值可能低于新鲜的数据,数据回送可能需要更多的下游 SGD 更新才能达到预期的表现。另一方面,每个下游步骤只需要 1/e(而不是 1)个上游步骤的时间。如果下游步骤增加的数量小于 e,上游步骤的总数(以及总训练时间)将减少。R 代表数据回送的最大可能加速,如果 e=R,并且重复数据和新数据价值相同,则可以实现最大加速。
考虑到训练过程中的每个操作都需要一些时间来执行,如果在 SGD 更新之前应用数据回送,R 能取最大值,但这将导致每个 epoch 多次使用同一批数据。然而,如果想在上游步骤和下游步骤之间找到更有利的权衡,更好的方式是较早的插入回送数据。
不同插入点的数据回送:
批处理前或批处理后的回送: 批处理前的回送是指数据在样本级别而不是批级别进行重复。这样增加了相邻批次不同的可能性,但代价是不能复制一批内的样本。批处理前回送的算法称为 样本回送(example echoing),批处理后回送的算法称为 批回送(batch echoing)。
数据增强前或数据增强后的回送: 数据增强前的回送允许重复数据进行不同的转换,能使重复数据更接近新数据。
数据回送的表现也受回送阶段后 shuffle 程度的影响。在适用的情况下,作者将 shuffle 作为缓冲区。缓冲区越大,shuffle 程度越高,训练算法能够近似于将整个训练集加载到内存中。
3、 实验
作者在两个语言建模任务、两个图像分类任务和一个目标检测任务上验证了数据回送的效果。对于语言建模任务,作者在 LM1B 和 Common Crawl 数据集上训练了 Transformer 模型。对于图像分类任务,作者在 CIFAR-10 数据集上训练了 ResNet-32 模型,在 ImageNet 数据集上训练了 ResNet-50 模型。对于目标检测任务,作者在 COCO 数据集上训练了 SSD 模型。
论文研究的主要问题是数据回送是否能够加速训练。作者用达到训练目标所需的“新鲜”样本数量衡量训练时间。因为新样本的数量与训练流程中上游步骤的数量成正比,因此,在回送因子小于或等于 r 时,新样本的数量与实际时间亦成正比。
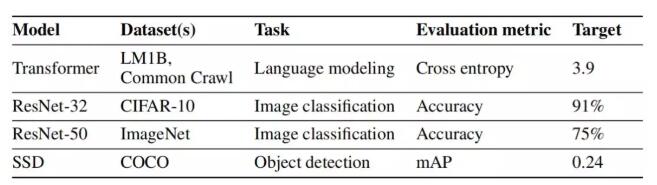
表 1 任务总结
对于任务,作者运行了一组没有数据回送的初始实验,并且调整参数以在实际计算预算内获得最佳的性能。作者选择了比初始实验中观察到的最佳值稍差的目标值。目标的微小变化并不会影响结论。表 1 总结了实验中使用的模型和目标值。
对每个实验,作者独立调整学习速率、动量和其它控制学习速率的参数。作者使用准随机搜索来调整元参数。然后选择使用最少的新样本达到目标值的试验。作者在每个搜索空间重复这个元参数搜索 5 次。实验结果中的所有图都显示了这 5 次实验所需的新样本的平均数,用误差条表示最小和最大值。
实验评估了在标准神经网络训练流程中添加数据回送的效果。作者实验了三种不同的数据回送:数据增强前的样本回送,增强后的样本回送,以及批回送。
3.1 数据回送可减少训练所需的新样本数量
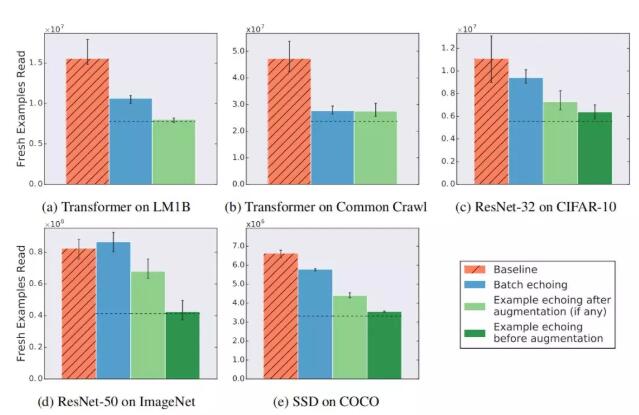
图 3 显示了表 1 中所有任务的数据回送效果,回送因子为 2。除一种情况外,所有情况下数据回送达到目标性能所需要的新样本数更少。唯一的例外(ResNet-50 上的批回送)需要与基线相同数量的新样本——说明数据回送虽然没有带来好处,但也不会损害训练。在训练中插入回送越早,所需的新样本就越少:与批回送相比,样本回送需要的新样本更少,并且数据增强之前的回送需要的新样本比增强之后回送需要的新样本更少。对于 ResNet-50 或 SSD,没有观察到数据回送和批归一化之间的任何负交互作用。
图 3 回送因子为 2 时,数据回送降低或不改变需要达到目标性能的新样本数量。点划线表示重复样本与新样本价值相同时的期望值。
3.2 数据回送可以缩短训练时间
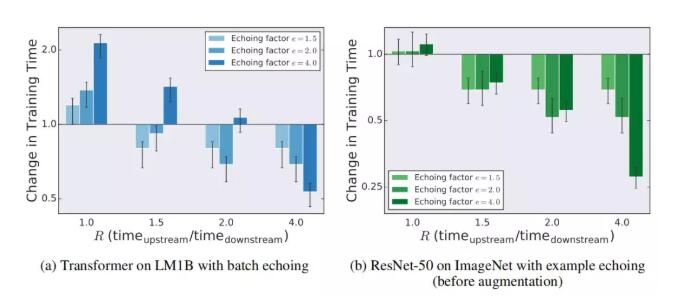
图 4 显示了不同的 R 值(上下游处理时间的比例)对应不同的回送因子 e 的训练时间变化。如果 R=1,数据回送会增加,或不像预期的那样显著缩短训练时间。如果 R>1,e≤r 的任何设置都能缩短训练时间,设置 e=R 可以最大程度地缩短训练时间。设置 e>R 不会缩短 LM1B 数据集上 Transformer 的训练时间,但它确实为 ImageNet 上的 ResNet-50 提供了加速。这些结果表明,围绕 e=R 的最佳值附近的回送因子,数据回送可以缩短训练时间,尤其是 e≤R 的设置。
图 4 不同 R 值对训练时间变化的影响
3.3 在回送因子的合理上限内,数据回送是有效的
图 5 显示了 Transformer 在 LM1B 上训练时,回送因子高达 16 的影响。批尺寸为 1024 时,最大有效回送因子介于 4 和 8 之间;超过此值,所需新样本的数量就会大于较小回送因子所需的样本数量。随着回送因子的增加,所需的新样本数量最终会超过基线,但即使是一个大于 16 的回送因子,所需的新样本仍然比基线少得多。批尺寸为 4096 时,最大有效回送因子甚至大于 16,这表明较大的批尺寸支持更大的回送因子。
图 5 回送因子上限为 16 时,样本回送减少了所需新样本的数量。点划线表示重复样本与新样本价值相同时的期望值。
3.4 批尺寸的增加对数据回送的影响
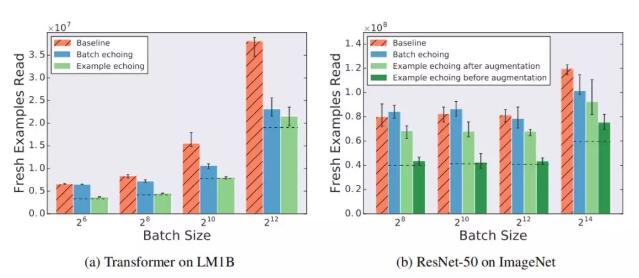
对于较大的批尺寸,批回送的性能更好,但样本回送有时需要更多的 shuffle 操作。图 6 显示了回送因子为 2 时,不同批尺寸的效果。随着批尺寸的增加,批回送的性能相对于基线保持不变或有所提高。这种影响是有道理的,因为随着批尺寸接近训练集的大小,重复的批数据会接近新的批数据,因此,在限制范围内,批回送必须通过回送因子减少所需的新样本数量。另一方面,图 6 显示了随着批尺寸增加,样本回送的性能相对于基线的要么保持不变,要么变差。这是由于随着批尺寸的增加,每批中重复样本的比例也随之增加,因此实际中,批尺寸较大的样本回送的表现可能更像较小的批尺寸的表现。较小的批尺寸可能会增加所需的 SGD 更新步数,这可以解释图 6 中的样本回送结果。增加重复样本的乱序数量(以增加内存为代价)可以提升较大批尺寸时样本回送的性能,因为降低了每批中重复样本的概率。
图 6 随批尺寸增加,批回送的表现相对于基线保持不变或有所提升,而样本回送的表现相对于基线保持不变或有所降低。点划线表示重复样本与新样本价值相同时的期望值。
3.5 Shuffle 程度越高,数据回送表现更好
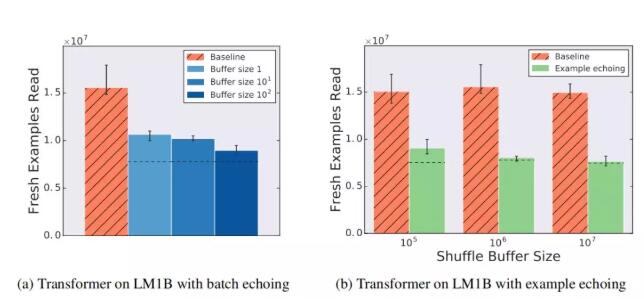
图 7 显示了增加数据回送的 shuffle 缓冲区大小(以增加内存为代价)的效果。虽然之前的所有批回送实验中没有 shuffle 操作,但如果重复批处理被打乱,批回送的性能会提高,而更多的乱序数量会带来更好的性能。同样,样本回送的性能也随着 shuffle 缓冲区大小的增加而提高,即使它对基线没有帮助。这是因为如第 3.4 节所述,更多的乱序数量降低了每批数据中重复样本的可能性。
图 7 shuffle 程度越高,数据回送的效果越好
3.6 数据回送不损害表现性能
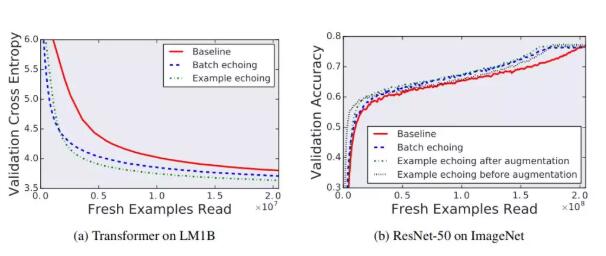
尽管人们可能担心重复使用数据可能会损害最终的表现性能,但实验中没有观察到任何类似情况。为了进一步证明数据回送不会降低解决方案的质量,作者在 LM1B 上使用 Transformer 进行了实验,在 ImageNet 上使用 Resnet-50 进行了实验,在固定新样本数量下找到最佳可实现性能。图 8 显示了在每个实验的训练过程中,数据回送在任何一点上都达到了最佳的性能。所有的数据回送变体都至少实现了与两个任务的基线相同的性能。
图 8 训练中的独立试验达到了最佳效果
4 、结论
数据回送是提高硬件利用率的一种简单策略。尽管先前研究人员担心重复数据的 SGD 更新是无用的,甚至是有害的。但是对于实验中的每一项任务,至少有一种数据回送方法能够减少需要从磁盘读取的样本数量。
数据回送是优化训练流程或额外上游数据处理的有效替代方案。尽管训练加速取决于模型结构、数据集、批尺寸以及重复数据的 shuffle 程度,但将回送因子设置为上下游处理时间的比率可以最大限度地提高潜在的加速速度,并在实验中取得了良好的效果。随着专业加速器(如 GPU 和 TPU)的改进速度继续超过通用计算的改进速度,数据回送以及类似的策略将成为神经网络训练工具包中越来越重要的组成部分。