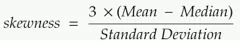数据科学实际上可定义为从数据中获取额外信息的过程。在进行数据科学研究时，真正想要达到的是一切数据在现实世界中的实际含义。
为提取复杂数据集中的信息，数据科学家采用了许多工具和技术，包括数据探索、可视化和建模。数据探索中，常用的一类非常重要的数学技术是统计学。
实际上，统计学可对数据概要进行具体而精确地定义。使用统计学，可以描述信息的部分属性，而非尝试描述每个数据点。因此统计学通常足以让人们获得有关数据结构和构成的某些信息。
有时，人们听到“统计”这个词时，往往会想得过于复杂。的确，这个词可能有点抽象，但并不总是需要通过复杂理论，才能从统计技术中获得某种价值。
统计学中最基本的部分通常是数据科学中最实用的部分。
今天，本文将概述5种有助于数据科学研究的统计学概念。这些概念没有那么抽象、令人抓狂，而是相当简单、适用的技术，作用颇大。
1. 集中趋势
数据集或特征变量的集中趋势是集的中心或典型值。我们的想法是，可能存在一单一值可(在某种程度上)***描述数据集。
例如，假设正态分布位于(100,100)的x-y位置。然后点(100,100)是集中趋势，因为在所有可供选择的点中，它是对数据进行概要的***点。
数据科学中可以用集中趋势方式，快速简单地了解数据集的整体情况。数据的“中心”可能是非常有价值的信息，告知数据集的确切偏差，因为在本质上，数据围绕的任何值都是偏差。以数学方式选择集中趋势有两种常用方法。
(1) 平均值
数据集的Mean值就是平均值，即整个数据围绕其展开的数字。在定义Mean时，用于计算平均值的所有值均需进行等量加权。
例如，计算以下5个数字的Mean值：
- (3+ 64 + 187 + 12 + 52) / 5 = 63.6
平均值非常适合计算实际数学平均值，也适用于像Numpy这样的Python库，计算速度非常快
(2) 中位数
中位数是数据集的中间值，即如果将数据从最小到***(或从***到最小)排序，然后取值该集中间的值：即中位数。
再次计算和上一组相同的5个数字的中位数：
- [3, 12, 52, 64, 187] → 52
中位数与平均值63.6完全不同。不能说两个数值孰对孰错，但人们可以根据自身情况和目标选择其一。
计算中位数需要对数据进行排序——如果数据集很大，那么这一做法就会变得不切实际。
此外，当异常值出现时，相较于平均值而言，中位数的数值更加稳定。因为如果出现一些非常极端的异常值，那么平均值将会变大或变小。
通过简单的numpy单行，可计算平均值和中位数
- numpy.mean(array)
- numpy.median(array)
2. 扩散
在统计学领域，数据传播是指数据被压缩为单一值或分布到更为广泛范围的程度。
查看下方的高斯概率分布图——假设这些图是描述现实世界中数据集的概率分布。
蓝色曲线的扩散值最小，因为其大多数数据点占据的范围相当窄。红色曲线的扩散值***，因为其大多数数据点占据的范围更广。
图例显示了这些曲线的标准偏差值，将在下一节中介绍。
(1) 标准偏差
标准偏差是量化数据传播最常用的方式。计算标准偏差包括5个步骤：
- 找出平均值。
- 对于每个数据点，计算其与平均值的差值的平方值。
- 将第2步得到的值相加。
- 除以数据点的数量。
- 取平方根。
较大值意味着数据从平均值更广泛地“展开”。较小值意味着数据越集中于平均值。
轻松计算Numpy的标准偏差：
- numpy.std(array)
3. 百分位数
使用百分位数进一步描述整个范围内每个数据点的位置。
就某数据点在数值范围内的高低位置而言，百分位数描述了该数据点的确切位置。
更正式地说，第p个百分位数是可分成两部分的数据集中的值。位置较低的部分包含数据的p%，即第p个百分位数。
例如，思考以下11个数字的集合：
- 1, 3, 5, 7, 9, 11,13, 15, 17, 19, 21
数字15是第70个百分位数，因为将数据集从数字15处，分成2个部分时，剩余数据中有70%的数据小于15。
百分位数与平均值和标准偏差相结合，有助于更好地了解特定数据点在数据扩散/范围内的位置。如果该数据点为异常值，那么其百分位数将接近终值——小于5%或大于95%。另一方面，如果百分位数的计算结果接近50，那么该数据点就接近于集中趋势。
数组的第50个百分位数可在Numpy中计算，如下所示：
- numpy.percentile(array,50)
4. 偏度
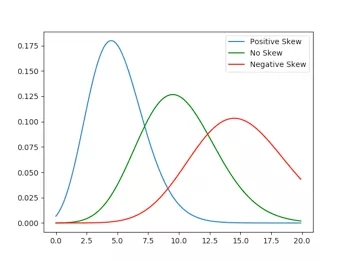
数据偏度是统计数据分布非对称程度的数字特征。
正偏意味着数值集中在数据点中心的左侧; 负偏意味着数值集中在数据点中心的右侧。
下图提供了一个很好的例证。
通过以下等式可计算偏度：
偏度计算了数据分布与高斯分布的距离。偏度值越大，高斯分布离数据集就越远。
这一点很重要，因为如果对数据分布有大概的了解，那么就可以为特定分布调整需要使用的任何ML模型。此外，并非所有ML建模技术都对高斯之外的数据有效。
进入建模前，统计学再次为人们提供了富有洞见的信息!
通过Scipy编程，计算偏度的方式如下：
- scipy.stats.skew(array)
5. 协方差和相关性
(1) 协方差
两个特征变量的协方差用于衡量两个变量如何“相关”。如果两个变量为协方差的正相关，那么当一个变量增加时，另一个变量也会增加;而在若为协方差的负相关，那么两个特征变量的值将在朝着相反方向改变。
(2) 相关性
相关性只是标准化的(缩放)协方差，除以需要分析的两个变量的标准偏差的乘积。这可使相关范围始终在-1.0和1.0之间。
如果两个特征变量的相关性为1.0，则变量具有***的正相关性。这意味着如果由于给定量，一个变量发生改变，则另一变量会按照相同方向成比例地移动。
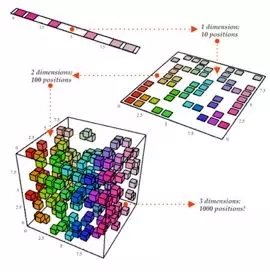
用于降维的PCA例证
正相关系数小于1表示不完全正相关，相关系数越接近1，相关性越强。这同样适用于负相关系数，只是特征变量的值在相反方向上变化，而非在相同方向上发生变化。
了解相关性对降维所拥的主成分分析(PCA)等技术非常有必要。人们首先计算一个相关矩阵——如果有两个或多个高度相关的变量，那么解释数据时，变量实际上是多余的，可删除其中一部分以降低复杂性。
