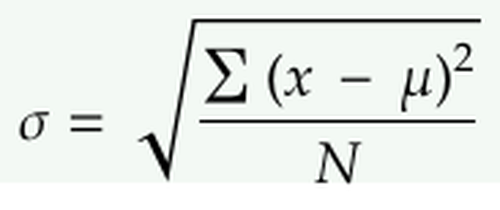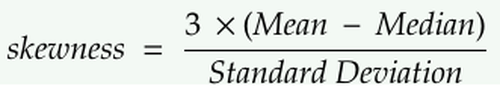数据科学实际上可以定义为我们从数据中获取额外信息的一个过程,在做数据科学时,我们真正想要做的其实就是解释除了数字之外,所有数据在现实世界中的实际含义。
为了提取潜藏在复杂数据集中的信息,数据科学家采用了许多工具和技术,包括数据挖掘、数据可视化和数据建模等等。数据挖掘中常用的一类非常重要的数学技术是统计学。
在实际意义上,统计数据允许我们定义数据的具体数学摘要。我们可以使用统计信息来描述其中的一些属性,而不是尝试描述每个数据点。而这通常足以让我们提取有关数据结构和构成的某些信息。
有些时候,当人们听到“统计”这个词时,往往会想到一些过于复杂的东西。也可能会有点抽象,但我们并非总是需要诉诸复杂的理论,来从统计中获得某种价值。
统计学中最基本的部分通常是数据科学中最实用的部分。
今天,我们将分享5个对于数据科学有用的统计学方法。这些不是过分抽象的概念,而是相当简单、有长期适用性的技术。
一、集中趋势(Central Tendency)
数据集或特征变量的集中趋势是集的中心或典型值。其思想是,可能有一个单一的值可以(在某种程度上)***地描述我们的数据集。
例如,假设你有一个以x-y位置(100,100)为中心的正态分布。那么点(100,100)是集中趋势,因为在所有可选择的点中,它提供了对数据***的总结。
对于数据科学来说,我们可以使用集中趋势进行度量,来快速简单地了解我们数据集的整体情况。我们的数据的“中心”可以是非常有价值的信息,它告诉我们数据集究竟是如何偏置的,因为数据所围绕的任何值本质上都是偏置。
在数学上有两种选择集中趋势的常用方法。
平均数(Mean)
平均数,也就是数据集的平均值,即整个数据围绕其进行散布的一个数字。在定义平均数时,所有用于计算平均数的值的权重都是相等的。
例如,计算以下5个数字的平均数:
- (3 + 64 + 187 + 12 + 52)/ 5 = 63.6
平均数非常适合计算实际数学平均值,使用像Numpy这样的Python库计算速度也非常快。
中位数(Median)
中位数是数据集的中间值,即我们将数据从最小值排序到***值(或从***值到最小值),然后取值集合中间的值:那就是中位数。
计算上一个例子中5个数字的中位数:
- [3,12,52,64,187]→ 52
中值与平均数完全不同。它们没有对错优劣之分,但我们可以根据我们的情况和目标选择一个。
计算中位数需要对数据进行排序——如果数据集很大,这会有点儿不切实际。
另一方面,中位数对于异常值比平均数更稳健,因为如果存在一些非常高的异常值,则平均值将被拉向某一个方向。
平均数和中位数可以用简单的numpy单行计算:
- numpy.mean(array)
- numpy.median(array)
二、扩散(Spread)
在统计学之下,数据的扩散是指指数据被压缩到一个或多个值的程度,这些值分布在更大的范围内。
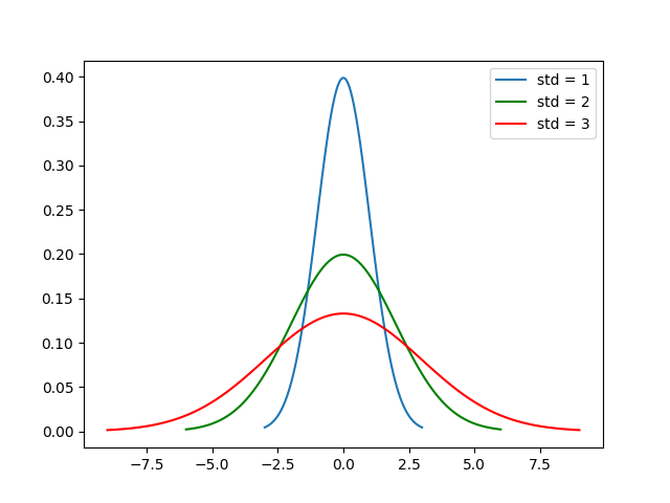
参考下面的高斯概率分布图——假设这些是描述真实世界数据集的概率分布。
蓝色曲线的扩散值最小,因为它的大部分数据点都在一个相当窄的范围内。红色曲线的扩散值***,因为大多数数据点所占的范围要大得多。
图例还显示了这些曲线的标准偏差,这将在下一节中介绍。
标准偏差(Standard Deviation)
标准偏差是定量数据扩散程度的最常见的方式。计算标准偏差需要5个步骤:
- 找到平均数。
- 对于每个数据点,求其与平均值间的距离的平方。
- 对步骤2中的值求和。
- 除以数据点的数量。
- 取平方根。
值越大,意味着我们的数据从平均数“扩散出去”的程度越高。值越小意味着我们的数据越集中于平均数。
计算Numpy的标准偏差:numpy.std(array)
三、百分位数(Percentiles)
我们可以使用百分位数进一步描述整个范围内每个数据点的位置。
百分位数根据数据点在值范围中的位置高低来描述数据点的确切位置。
更正式地说,第p百分位数是数据集中的一个值,在该值处可以将数据集分为两部分。下半部分包含p %个数据,则称其为第p百分位数。
例如以下11个数字的集合:
- 1,3,5,7,9,11,13,15,17,19,21
数字15就是是第70百分位数,因为当我们在数字15处将数据集分成两部分时,有70%个数据小于15。
百分位数与平均数和标准偏差相结合,可以让我们很好地了解特定的点在数据集的扩散/范围内的位置。如果它是一个异常值,那么它的百分位数将接近于终点——小于5%或大于95%。另一方面,如果百分位数接近50那么我们就可以知道它非常接近集中趋势。
数组的第50个百分位数在Numpy中计算:numpy.percentile(array, 50)
四、斜度(Skewness)
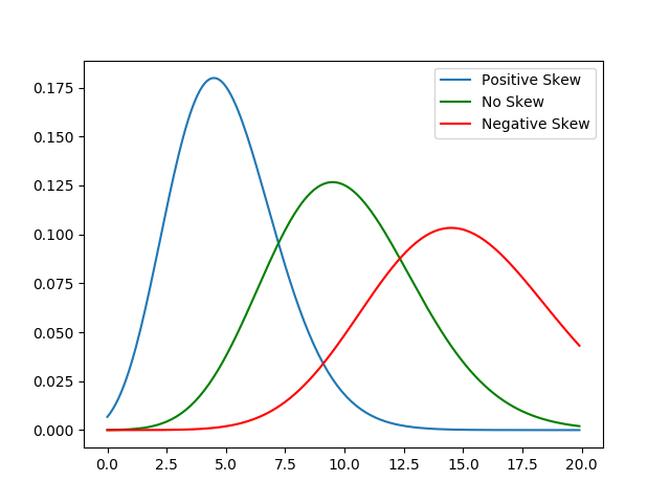
数据的偏斜度衡量其不对称性。
偏度为正值,表示值集中在数据点中心的左侧;负偏度表示值集中在数据点中心的右侧。
下图提供了一个很好的说明。
我们可以用以下等式计算偏斜度:
偏斜度可以让我们知道数据分布与高斯分布的距离。偏斜度越大,我们的数据集离高斯分布越远。
这很重要,因为如果我们对数据的分布有一个粗略的概念,我们就可以为特定的分布定制我们要训练的ML模型。此外,并非所有ML建模技术都能对非高斯数据有效。
再次提醒大家,在我们开始建模之前,统计数据能够带给我们非常富有洞察力的信息!
如何在Scipy代码中计算偏斜度: scipy.stats.skew(array)
五、协方差(Covariance)和相关系数(Correlation)
协方差
两个特征变量的协方差衡量它们之间的相关性。如果两个变量有正协方差,那么当一个变量增加时,另一个也会增加;当协方差为负时,特征变量的值将向相反的方向变化。
相关系数
相关系数简单来说就是标准化(缩放)的协方差,除以被分析的两个变量的标准偏差的乘积即可得到。这有效地迫使关联范围始终在-1.0和1.0之间。
如果两个特征变量的相关系数为1.0,则两个特征变量的相关系数为正相关。这意味着,如果一个变量的变化量是给定的,那么第二个变量就会按比例向相同的方向移动。
当正相关系数小于1时,表示正相关系数小于完全正相关,且相关强度随着数字趋近于1而增大。同样的思想也适用于负相关值,只是特征变量的值在相反的方向变化,而不是在相同的方向变化。
了解相关性对于主成分分析(PCA)等降维技术非常有用。我们从计算一个相关矩阵开始——如果有两个或两个以上的变量高度相关,那么它们在解释我们的数据时实际上是冗余的,可以删除其中一些变量以降低复杂性。