我们使用统计数据(通常以不合适的方式)来揭示战争伤亡人数的增加或减少,提醒公众注意发病率的变化,测量一种新产品的销量,判断某一只股票的赚钱能力,决定下一张牌是A的概率,衡量不同大学的毕业率,记录不同年龄段的人们性生活的频率,为很多其他问题提供资源和信息。
统计数据(statistics)就是用数字表达出来的证据。这样的证据可能看起来非常动人,因为数字让证据显得非常有科学性,非常精确,似乎它就代表了“事实”。但是,统计数据能,而且经常会,撒谎!它们并不必然就能证明它们想要证明的一切。
两种不同的提供数据的方式有可能会产生欺骗性:
小贴士:统计数据可能而且经常骗人。它们并不必然就能证明表面上想要证明的一切。
作为一个会思考和判断的人,你应该努力辨别出错误的统计数据式的论证。在几个较短的段落中,我们无法向你全面展示人们用“统计数据帮忙撒谎”的所有不同方法。但是,本文我们将为你提供一些基本策略,这样你就可以用来发现这些骗人的小伎俩。
同时,它还通过展示许多作者错误使用统计数字来当证据的最常见的方法,提醒你注意数据论证中存在的缺陷。
关键问题:数据有没有欺骗性?
01 不知来历和带有偏见的数据
最近的一个新闻标题:40%的大学生饱受抑郁症的折磨!
在你情绪低落的时候你该不该过分担心呢?你又怎么知道自己可以相信这样的统计数字?
任何统计数字都要求发生在某地的某些事件能被界定并准确识别出来,这常常是一项非常艰巨的任务。因此,要找出欺骗性的数据,第一个策略就是尽量找到足够多的关于这些数据是如何采集的信息。
我们能不能准确地知道美国到底有多少人在报税单上做过手脚,多少人有过婚前性行为,多少人开车打手机,或多少人使用违禁药品?如果你想象一下做这些统计的细枝末节,那么我们怀疑你的答案肯定会是“不太可能”。
为什么?因为要为特定的目的得到精确的数据,你常常会遇到各种各样的拦路虎和绊脚石,其中包括关键词语的模棱两可,识别相关人员或事件的种种困难,人们不愿意提供真实的信息,不能报告各种事件,还有观察事件时存在的种种身体上的障碍等。
因此,统计数据的形式往往只能是基于事实做出的一些估计。这些估计有时候很有用,但它们也可能有欺骗性。记住总要问一问,“作者是怎样得出这个估计的?”得到的细节越多越好。
不知来历的统计数字最常见的一个用处就是用大量的数字给别人加深印象或让别人肃然起敬,这些呈现出来的数字的精确性常常会让人怀疑。比如说,大量的数字可能被用来提醒公众注意日渐增长的身体失调或精神失常的发生率,例如癌症、饮食异常或幼年孤僻症等。
如果我们能知道这些数据确定的过程是如何得谨慎,我们肯定更会深受这些数据的感染。比如说,一直以来人们都在努力统计大学生抑郁症发病率的准确数字,但是不知来历的数据问题已经成为影响统计的一个主要因素,研究报上来的发病率在10%~40%之间。
所以,本部分一开始提到的那份研究如果让你觉得过度惊慌的话,那你未免显得有些杯弓蛇影。记住:在对这样的数据做出反应之前,我们先要问一问它们是怎么得来的。
02 令人困惑的平均值
请检查下面的陈述:
- 快速致富的一个方法就是做一名职业足球队员,2010年国家足球联盟球星的平均收入是180万美元。
- 在大学里取得好成绩,学生需要付出的努力越来越少了。根据最近一项调查,大学生每周平均花在学习上的时间是12.8小时,和20年前的大学生相比大概只有他们的一半。
两个例子当中都使用了“平均”这个词。但是实际上却有三种不同的方法来测定平均值,而且在大多数情况下,每种方法都会给出不同的数值。
- 第一种方法是把所有数值相加,然后用总数除以相加的数目。这种方法所得的结果就是平均数(mean)。
- 第二种方法是将所有数值从高到低排列,然后找到位于最中间的数值,这个中间数值就是中位数(median)。有一半的数值在中位数之上,另一半在中位数下面。
- 第三种方法是将所有数值排列好,计算每个不同数值出现的次数或每个不同数值范围出现的次数,出现频率最高的数值就叫作众数(mode),这是第三种平均值。
作者谈论的是平均数、中位数还是众数,将会产生很大的区别。
平均值的种类:
- 平均数:通过把所有数值相加然后用总数除以相加的数目来计算
- 中位数:通过将所有数值从高到低排列然后找到位于最中间的数值来测定
- 众数:通过计算不同数值出现的次数然后找出出现频率最高的数值的方法来测定
第一个例子当中取什么平均值最能说明问题?请考虑一下职业化运动当中大牌球星的收入与那些一般球员的收入对比。最大牌的球星,比如说橄榄球明星四分卫,收入比球队里大部分其他球员要高出很多。
事实上,2010年度薪酬最高的橄榄球运动员岁入超过1 500万美元,而这远远高于平均值。这样高的收入将会急剧拉高平均数,但是对于中位数或众数而言则影响不大。
举例来说,国家橄榄球联盟的球员2010年度工资平均数是180万美元,但是其工资中位数却只有77万美元。因此,在大部分职业运动当中,平均数工资要比中位数工资或者众数工资高出很多。所以,如果有人想让工资水平显得非常非常高,他就会选择平均数作为平均值。
现在让我们来仔细看看第二个例子。如果这里列举的平均值要么是中位数要么是众数,我们有可能就高估了平均的学习时间。有些学生很可能花了极多的学习时间,比如一周30或40个小时,这样就提高了平均数的数值,但是却不影响中位数或者众数的数值。学习时间的众数数值可能远低于或远高于中位数,主要取决于多长的学习时间对学生而言最为常见。
当你见到平均值的时候,一定要记得问一下:“是平均数、中位数还是众数,平均值的含义不同会不会产生什么影响?”要回答这个问题,请想一想平均值的不同含义会给信息的意义带来怎样的变化。
不仅判断一个平均值是平均数、中位数还是众数非常重要,判定最小数值和最大数值之间的差距,即全距(range)以及每个数值出现的频率,也就是数值分布,常常也显得异常重要。
下面我们来看一个例子,在这个例子里知道数值的全距和分布就显得非常重要。
医生对20岁的病人说:你所患癌症的预后不容乐观。患同样癌症的病人存活时间的中位数是10个月。所以剩下来的这几个月你想做什么就做点什么吧,不必有什么顾虑了。
病人听到医生给出这样的诊断结果,对自己的未来该做出怎样可怕的展望呢?首先,我们确定知道的是获得这种诊断的病人有一半不到10个月就去世了,还有一半人存活时间超过了10个月。
但是我们并不知道活下来的那部分人的存活时间的全距和数值分布。也许存活时间超过10个月的病人的数值全距和分布会显示,有些人、甚至很多人活得远远超过了10个月的时间。其中有些人、甚至很多人可能活到80岁以上呢!知道病人存活情况的完整分布可能会改变这个癌症患者对未来的看法。
一般来说,病人应该考虑国内不同的医院对于他的疾病的存活率是不是有不同的全距和数值分布。这样的话,他就应该考虑选择在那家有最乐观的数值分布情况的医院就诊。
当我们遇到平均数的时候,记住全距和数值分布的一个总体好处,就是这样做会提醒你,大多数人或事并不完全符合确切的平均值,与平均数值差异极大的结果也在预料之中。
例如,很多旨在促进我们健康状况的干预措施,都会展示某些健康手段的平均获益情况,尽管参与这项研究的许多人获益极少或基本没有获益,有些人甚至还会不同程度地受损。
03 把一件事的结论用来证明另一件事
有些数据确实能证明一件事,而立论者往往宣称这些数据证明了另一件性质完全不同的事,这时候他们往往在欺骗我们。这些数据压根儿就证明不了它们用来证明的一切!有两种策略可以帮你找出这类欺骗。
一个策略就是对立论者提供的数据视而不见,然后问自己:“什么样的统计数据作证据,在证明他的结论时会有帮助?”然后,将“所需”的数据和给出的数据进行比较。如果两者之间难以吻合,你可能就发现了一个数据上的欺骗。下面的例子为你提供一个机会来应用这种策略。
如果你乘坐我们这座城市的地铁,十有八九你的手机会被人偷走。我刚读到一份统计数字,说小的电子产品占到地铁系统失窃率的70%。
需要做什么样的研究才能获得个好主意,可以知道自己乘地铁时电子产品被人偷走的可能性到底有多大。你自然想知道乘地铁被偷的概率,而不是被偷走电子产品的概率。这个数据证明了一件事,即地铁系统的大部分偷窃行为都是奔着小电子产品去的。但它并没有证明这类偷窃行为发生的概率有多大。
要回答这个问题,你需要这样问,在坐地铁的时候被偷的概率到底是多少?有可能总体的偷窃行为非常少,但是其中大部分都牵涉到小电子产品。从这个例子当中得到的最重要的教训就是:我们一定要加倍注意统计数据和结论的措辞,看看二者是不是指的同一件事情。如果不是,作者或演说者就很可能是在用数据说谎。
知道什么样的数据证据应被用来支持一个结论是很难的。因此,另一个策略就是不急于去看作者的结论,而是先仔细检查作者的数据,然后问自己,“从这些数据我们可以得出什么合适的结论?”然后拿你的结论和作者的结论相比较。请用这个策略来检验下面这个例子。
大约半数的美国人欺骗了自己的另一半。研究人员最近在一家购物中心采访了很多人。在接受采访的75人当中,有36人坦承他们有朋友曾承认欺骗过自己的约会对象。
你有没有想到这个例子一开始得出的结论?大约一半人在某个特定地点承认有朋友告诉过自己,他们在和他人约会或交往过程中至少有过一次欺骗行为。你有没有看出数据所证明的东西和作者的结论之间存在着巨大的差异?如果你看出来了,那你就发现了这位作者是如何利用数据来撒谎和欺骗的。
04 通过省略信息欺骗
统计数据经常因为不完整而欺骗了我们。因此,另一个在数据论证中找到缺陷的非常有用的策略就是问一问:“在判断数据的影响力之前,还需要什么进一步的信息?”让我们先看看下面的例子,展示一下这个问题所起的作用。
- 大公司正在将市中心地带的小镇气息破坏殆尽。就在去年,城里的大公司的数目增长了75%。
- 尽管大家都挺害怕,但跳伞运动其实比其他活动比如说驾驶汽车要安全得多。拿某一个月的时间来作比较,这段时间里,洛杉矶有176人死于车祸,而死于跳伞事故的却只有3人。
- 艾滋病预防项目需要较大的资金增幅。2009年,有54 000人饱受艾滋病的折磨。
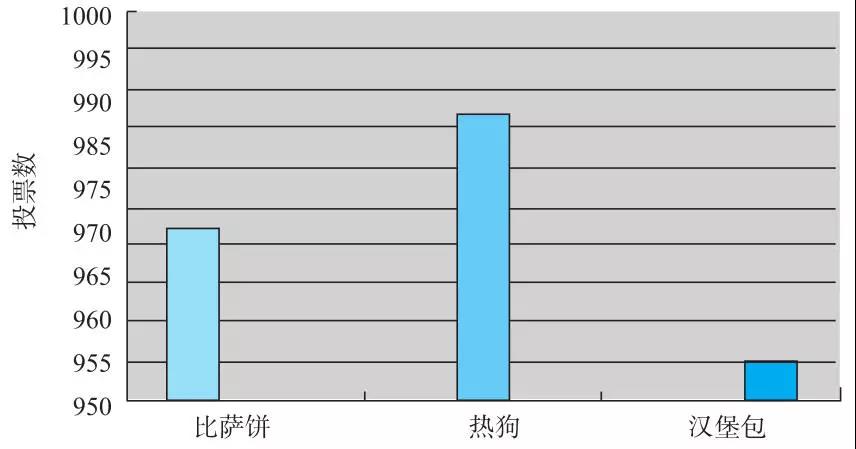
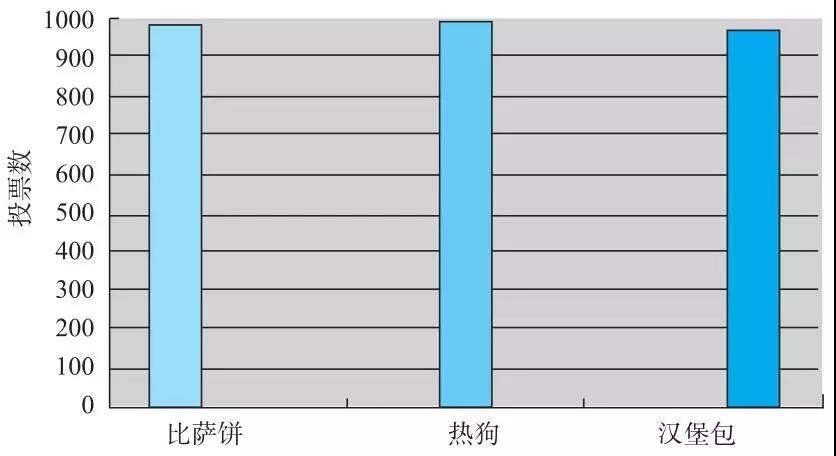
第一个例子中,75%这个数字很吸引眼球。但是缺少了一些东西:这个百分比所依据的绝对数值。假如我们知道这种增长是从4家增长到7家,而不是从12家增长到21家,我们还会觉得如此惊讶吗?
在第二个例子里,我们倒是有数字了,但是却不知道比率。难道我们不需要知道这些数字对参加这两种活动的人数的百分比来说有什么意义吗?不论怎样,参加跳伞活动的总人数比起驾车的总人数而言简直是微不足道。
第三个例子展示了我们社会中常见的一个事实,通过聚焦全国范围内受病痛折磨的总人数,企图引起公众对某个社会问题的关注。尽管这显然是个亟待解决的问题,但当我们将54 000除以美国的大概总人口3亿人,我们只得到一个大概0.02%的数值。
当你遇到听起来让人动心的数字或者百分比,一定要当心!你可能需要其他信息来判定这些数字到底有多让人动心!当只有绝对数值摆在眼前的时候,问一问知道百分比是不是有可能帮你做出更好的判断;当只有百分比出现在眼前的时候,问一问是不是绝对数值会丰富它们的含义。
当你遇到统计数字的时候,一定要记得问一问:“缺少了什么相关信息?”
关于作者:
尼尔·布朗,博林格林州立大学(Bowling Green State University)的杰出经济学教授。获有托雷多大学法学博士学位和得克萨斯大学的博士学位。
斯图尔特·基利,美国伊利诺伊大学心理学博士。现为美国博林格林州立大学心理学教授。