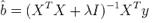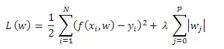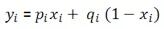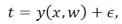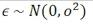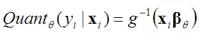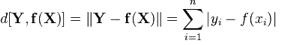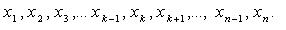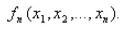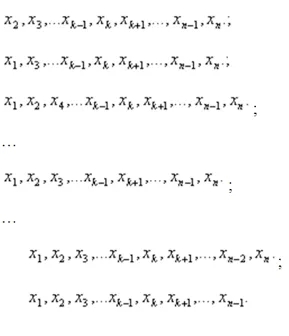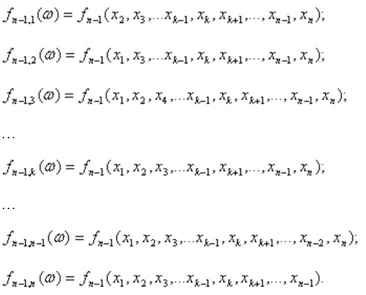除了统计模型和其他的一些算法,回归是机器学习成功运行的重要构成要素。回归的核心是寻找变量之间的关系,而机器学习需要根据这种关系来预测结果。
显然,任何称职的机器学习工程师都应重视回归,但回归也有很多种。线性回归和逻辑回归通常是人们最先学习的算法,然而还有许多回归类型。每种类型都有各自的重要性,并且有最适合应用的情境。那么,该用哪一种呢?
本文将用通俗易懂的方式介绍最常用的回归类型,遇到具体任务时你便知晓该使用哪一种。
1. 线性回归Linear regression
线性回归是最典型的回归类型,大约250年前就已出现,也被称为普通最小二乘法(OLS)和线性最小二乘法回归。可以使用它对小数据集进行计算,甚至可以手动计算。目前线性回归常用于插值,但不适合实际预测和主动分析。
另外,现代数据常常结构混乱,线性回归容易“滞后”:线性回归过于精确。如果模型对一组数据计算精确,对另一组数据却极不精确,而线性回归本应描述一般模式,过于精确会使其在几乎所有情况下变得不稳定。
2. 岭回归Ridge regression
岭回归是线性回归的重要改进,增加了误差容忍度,对回归系数进行了限制,从而得到更加真实的结果,并且结果更容易解释。该方法用于解决自变量之间相互关联(多重共线性)时的数据冗余问题。
岭回归需要使用如下公式来评估参数:
3. 套索回归Lasso-regression
套索回归与岭回归类似,但回归系数可为0(模型中排除了一些符号)。
4. 偏最小二乘法回归Partial least squares(PLS)
与自变量数目相比,观察结果很少时,或者自变量高度相关时,PLS会很有用。PLS可将自变量减少,并使其不相关,类似于主成分分析。然后,对这些自变量而非原始数据进行线性回归。
PLS强调发展预测模型,不用于筛选变量。与OLS不同,PLS可以包含多个连续因变量。PLS利用相关结构识别较小的效应,并对因变量中的多元模式进行建模。
来源:Pexels
5. 逻辑回归Logistic regression
逻辑回归广泛应用于临床试验、量化,或者欺诈分析——当测试药物或信用卡交易的信息可以二进制形式(是/否)获得时。线性回归固有的缺点它也有,如低误差容忍度、依赖数据集,但总的来说,逻辑回归更好,并且可以简化为线性回归类型来简化计算。有些版本如泊松回归得到了改进,以便有时需要得到非二进制答案,例如分类、年龄组、甚至回归树。
6. 生态回归 Ecological Regression
生态回归用于将数据划分为相当大的层或组的情况(回归分别应用于每个层或组),例如,在政治学中生态回归用于根据汇总数据评估选民的群体行为。
然而,应该警惕“大数据的诅咒”:如果对数百万次回归进行统计,其中一些模型可能完全不准确,成功的模型将被高度(且人为)一致的嘈杂模型“击溃”。因此,这种类型的回归不适合预测极端事件(地震)和研究因果关系(全球变暖)。
7. 贝叶斯线性回归Bayesian linear regression
贝叶斯线性回归与岭回归类似,但它的前提是所有可能的误差都服从正态分布。因此,假设对数据结构有基本了解,就可能获得更精确的模型(特别是与线性回归相比)。
然而,在实际操作中,若处理大数据,对数据的初始了解并不能保证准确性,所以这种假设是基于共轭值的,即本质上是人为的,这是这种回归类型的一个显著缺陷。
观测变量的计算:
误差服从正态分布:
8. 分位数回归Quantile regression
分位数回归用于极端事件,包括故意在结果中引入偏差,从而提高模型的准确性。
9. 最小绝对偏差Least absolute deviations(LAD)
最小绝对偏差也称为最小绝对误差(LAE)、最小绝对值(LAV)、最小绝对残差(LAR)、绝对偏差之和或L1范数条件,是最小的模量方法。它用于从包含随机误差的测量值中评估未知值,以及估算给定函数的表示法(近似值)。最小绝对偏差看起来像线性回归,但使用的是绝对值而不是平方。因此,模型的准确性有所提高,且没有使计算复杂化。
10. 刀切法重采样Jackknife resampling(大折刀法)
刀切法重采样是一种用于聚类和数据细化的新型回归方法。这种方法不具有典型回归类型的缺点,能为回归问题提供近似但非常准确、抗误差的解决方案,自变量相关或不“服从”正态分布时都可使用。
这种类型的回归很适合黑盒类型预测算法,它非常接近线性回归,没有精度损失,即使传统回归假设(变量不相关、数据正态分布、条件方差恒定)由于数据性质不被接受,它依旧可以使用。
假设样本如下:
在概率统计理论中,假设这是一组独立同分布的随机变量,且以下是要研究的数据:
约翰•图基(John Tukey)在1949年提出的观点(即“大折刀法”)是对一个样本做大量的研究,排除一个观察结果(并返回之前被排除的结果)。下面列出了从原始数据中获得的样本:
每一项都有n个新样本,样本容量为n-1,且都可用来计算计量经济学感兴趣的统计数据的价值(样本容量减1):
通过获得的统计值,可了解其分布和分布的特征,如期望、中值、分位数、散点和均方差。
那么,该使用哪一种回归?
- 如果模型需要连续的因变量:线性回归是最常见和最直接的使用类型。如果有一个连续的因变量,可能要首先考虑线性回归模型。然而,要注意线性回归的几个缺点,如对异常值和多重共线性很敏感。在这种情况下,最好使用更高级的线性回归变体,如岭回归、套索回归和偏最小二乘法回归(PLS)。
- 如果模型需要分类因变量:应使用逻辑回归。这种模型最适合二元因变量。在进行更复杂的分类建模之前,最好先使用这种模型。分类变量的有些值可以根据特征放入可计数的不同组中。逻辑回归对因变量进行变换,然后使用最大似然估计法而非最小二乘法来估计参数。
- 如果模型需要计数因变量:应使用泊松回归。计数数据往往遵循泊松分布,因此泊松回归很适合。使用泊松变量可以计算和评估发生率。