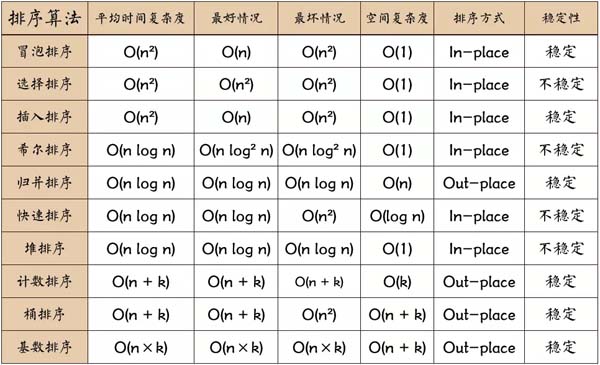
本文内容包括:(双向)冒泡排序、选择排序、插入排序、快速排序(填坑和交换)、归并排序、桶排序、基数排序、计数排序(优化)、堆排序、希尔排序。大家可以在这里测试代码。更多 leetcode 的 JavaScript 解法也可以在我的算法仓库中找到,欢迎查看~
另外附上十大排序的 C++版本,因为写惯了JavaScript,所以这个 C++版本写得有些丑,请不要介意呀。
如果你觉得有帮助的话,就点个 star 鼓励鼓励我吧,蟹蟹😊
先推荐一个数据结构和算法动态可视化工具,可以查看各种算法的动画演示。下面开始正文。
冒泡排序
通过相邻元素的比较和交换,使得每一趟循环都能找到未有序数组的***值或最小值。
***:O(n),只需要冒泡一次数组就有序了。
最坏:O(n²)
平均:O(n²)
单向冒泡
- function bubbleSort(nums) {
- for(let i=0, len=nums.length; i<len-1; i++) {
- // 如果一轮比较中没有需要交换的数据,则说明数组已经有序。主要是对[5,1,2,3,4]之类的数组进行优化
- let mark = true;
- for(let j=0; j<len-i-1; j++) {
- if(nums[j] > nums[j+1]) {
- [nums[j], nums[j+1]] = [nums[j+1], nums[j]];
- mark = false;
- }
- }
- if(mark) return;
- }
- }
双向冒泡
普通的冒泡排序在一趟循环中只能找出一个***值或最小值,双向冒泡则是多一轮循环既找出***值也找出最小值。
- function bubbleSort_twoWays(nums) {
- let low = 0;
- let high = nums.length - 1;
- while(low < high) {
- let mark = true;
- // 找到***值放到右边
- for(let i=low; i<high; i++) {
- if(nums[i] > nums[i+1]) {
- [nums[i], nums[i+1]] = [nums[i+1], nums[i]];
- mark = false;
- }
- }
- high--;
- // 找到最小值放到左边
- for(let j=high; j>low; j--) {
- if(nums[j] < nums[j-1]) {
- [nums[j], nums[j-1]] = [nums[j-1], nums[j]];
- mark = false;
- }
- }
- low++;
- if(mark) return;
- }
- }
选择排序
和冒泡排序相似,区别在于选择排序是将每一个元素和它后面的元素进行比较和交换。
***:O(n²)
最坏:O(n²)
平均:O(n²)
- function selectSort(nums) {
- for(let i=0, len=nums.length; i<len; i++) {
- for(let j=i+1; j<len; j++) {
- if(nums[i] > nums[j]) {
- [nums[i], nums[j]] = [nums[j], nums[i]];
- }
- }
- }
- }
插入排序
以***个元素作为有序数组,其后的元素通过在这个已有序的数组中找到合适的位置并插入。
***:O(n),原数组已经是升序的。
最坏:O(n²)
平均:O(n²)
- function insertSort(nums) {
- for(let i=1, len=nums.length; i<len; i++) {
- let temp = nums[i];
- let j = i;
- while(j >= 0 && temp < nums[j-1]) {
- nums[j] = nums[j-1];
- j--;
- }
- nums[j] = temp;
- }
- }
快速排序
选择一个元素作为基数(通常是***个元素),把比基数小的元素放到它左边,比基数大的元素放到它右边(相当于二分),再不断递归基数左右两边的序列。
***:O(n * logn),所有数均匀分布在基数的两边,此时的递归就是不断地二分左右序列。
最坏:O(n²),所有数都分布在基数的一边,此时划分左右序列就相当于是插入排序。
平均:O(n * logn)
参考学习链接:
算法 3:最常用的排序——快速排序
三种快速排序以及快速排序的优化
快速排序之填坑
从右边向中间推进的时候,遇到小于基数的数就赋给左边(一开始是基数的位置),右边保留原先的值等之后被左边的值填上。
- function quickSort(nums) {
- // 递归排序基数左右两边的序列
- function recursive(arr, left, right) {
- if(left >= right) return;
- let index = partition(arr, left, right);
- recursive(arr, left, index - 1);
- recursive(arr, index + 1, right);
- return arr;
- }
- // 将小于基数的数放到基数左边,大于基数的数放到基数右边,并返回基数的位置
- function partition(arr, left, right) {
- // 取***个数为基数
- let temp = arr[left];
- while(left < right) {
- while(left < right && arr[right] >= temp) right--;
- arr[left] = arr[right];
- while(left < right && arr[left] < temp) left++;
- arr[right] = arr[left];
- }
- // 修改基数的位置
- arr[left] = temp;
- return left;
- }
- recursive(nums, 0, nums.length-1);
- }
快速排序之交换
从左右两边向中间推进的时候,遇到不符合的数就两边交换值。
- function quickSort1(nums) {
- function recursive(arr, left, right) {
- if(left >= right) return;
- let index = partition(arr, left, right);
- recursive(arr, left, index - 1);
- recursive(arr, index + 1, right);
- return arr;
- }
- function partition(arr, left, right) {
- let temp = arr[left];
- let p = left + 1;
- let q = right;
- while(p <= q) {
- while(p <= q && arr[p] < temp) p++;
- while(p <= q && arr[q] > temp) q--;
- if(p <= q) {
- [arr[p], arr[q]] = [arr[q], arr[p]];
- // 交换值后两边各向中间推进一位
- p++;
- q--;
- }
- }
- // 修改基数的位置
- [arr[left], arr[q]] = [arr[q], arr[left]];
- return q;
- }
- recursive(nums, 0, nums.length-1);
- }
归并排序
递归将数组分为两个序列,有序合并这两个序列。
***:O(n * logn)
最坏:O(n * logn)
平均:O(n * logn)
参考学习链接:
图解排序算法(四)之归并排序
- function mergeSort(nums) {
- // 有序合并两个数组
- function merge(l1, r1, l2, r2) {
- let arr = [];
- let index = 0;
- let i = l1, j = l2;
- while(i <= r1 && j <= r2) {
- arr[index++] = nums[i] < nums[j] ? nums[i++] : nums[j++];
- }
- while(i <= r1) arr[index++] = nums[i++];
- while(j <= r2) arr[index++] = nums[j++];
- // 将有序合并后的数组修改回原数组
- for(let t=0; t<index; t++) {
- nums[l1 + t] = arr[t];
- }
- }
- // 递归将数组分为两个序列
- function recursive(left, right) {
- if(left >= right) return;
- // 比起(left+right)/2,更推荐下面这种写法,可以避免数溢出
- let mid = parseInt((right - left) / 2) + left;
- recursive(left, mid);
- recursive(mid+1, right);
- merge(left, mid, mid+1, right);
- return nums;
- }
- recursive(0, nums.length-1);
- }
桶排序
取 n 个桶,根据数组的***值和最小值确认每个桶存放的数的区间,将数组元素插入到相应的桶里,***再合并各个桶。
***:O(n),每个数都在分布在一个桶里,这样就不用将数插入排序到桶里了(类似于计数排序以空间换时间)。
最坏:O(n²),所有的数都分布在一个桶里。
平均:O(n + k),k表示桶的个数。
参考学习链接:
拜托,面试别再问我桶排序了!!!
- function bucketSort(nums) {
- // 桶的个数,只要是正数即可
- let num = 5;
- let max = Math.max(...nums);
- let min = Math.min(...nums);
- // 计算每个桶存放的数值范围,至少为1,
- let range = Math.ceil((max - min) / num) || 1;
- // 创建二维数组,***维表示第几个桶,第二维表示该桶里存放的数
- let arr = Array.from(Array(num)).map(() => Array().fill(0));
- nums.forEach(val => {
- // 计算元素应该分布在哪个桶
- let index = parseInt((val - min) / range);
- // 防止index越界,例如当[5,1,1,2,0,0]时index会出现5
- indexindex = index >= num ? num - 1 : index;
- let temp = arr[index];
- // 插入排序,将元素有序插入到桶中
- let j = temp.length - 1;
- while(j >= 0 && val < temp[j]) {
- temp[j+1] = temp[j];
- j--;
- }
- temp[j+1] = val;
- })
- // 修改回原数组
- let res = [].concat.apply([], arr);
- nums.forEach((val, i) => {
- nums[i] = res[i];
- })
- }
基数排序
使用十个桶 0-9,把每个数从低位到高位根据位数放到相应的桶里,以此循环***值的位数次。但只能排列正整数,因为遇到负号和小数点无法进行比较。
***:O(n * k),k表示***值的位数。
最坏:O(n * k)
平均:O(n * k)
参考学习链接:
算法总结系列之五: 基数排序(Radix Sort)
- function radixSort(nums) {
- // 计算位数
- function getDigits(n) {
- let sum = 0;
- while(n) {
- sum++;
- n = parseInt(n / 10);
- }
- return sum;
- }
- // ***维表示位数即0-9,第二维表示里面存放的值
- let arr = Array.from(Array(10)).map(() => Array());
- let max = Math.max(...nums);
- let maxDigits = getDigits(max);
- for(let i=0, len=nums.length; i<len; i++) {
- // 用0把每一个数都填充成相同的位数
- nums[i] = (nums[i] + '').padStart(maxDigits, 0);
- // 先根据个位数把每一个数放到相应的桶里
- let temp = nums[i][nums[i].length-1];
- arr[temp].push(nums[i]);
- }
- // 循环判断每个位数
- for(let i=maxDigits-2; i>=0; i--) {
- // 循环每一个桶
- for(let j=0; j<=9; j++) {
- let temp = arr[j]
- let len = temp.length;
- // 根据当前的位数i把桶里的数放到相应的桶里
- while(len--) {
- let str = temp[0];
- temp.shift();
- arr[str[i]].push(str);
- }
- }
- }
- // 修改回原数组
- let res = [].concat.apply([], arr);
- nums.forEach((val, index) => {
- nums[index] = +res[index];
- })
- }
计数排序
以数组元素值为键,出现次数为值存进一个临时数组,***再遍历这个临时数组还原回原数组。因为 JavaScript 的数组下标是以字符串形式存储的,所以计数排序可以用来排列负数,但不可以排列小数。
***:O(n + k),k是***值和最小值的差。
最坏:O(n + k)
平均:O(n + k)
- function countingSort(nums) {
- let arr = [];
- let max = Math.max(...nums);
- let min = Math.min(...nums);
- // 装桶
- for(let i=0, len=nums.length; i<len; i++) {
- let temp = nums[i];
- arr[temp] = arr[temp] + 1 || 1;
- }
- let index = 0;
- // 还原原数组
- for(let i=min; i<=max; i++) {
- while(arr[i] > 0) {
- nums[index++] = i;
- arr[i]--;
- }
- }
- }
计数排序优化
把每一个数组元素都加上 min 的相反数,来避免特殊情况下的空间浪费,通过这种优化可以把所开的空间大小从 max+1 降低为 max-min+1,max 和 min 分别为数组中的***值和最小值。
比如数组 [103, 102, 101, 100],普通的计数排序需要开一个长度为 104 的数组,而且前面 100 个值都是 undefined,使用该优化方法后可以只开一个长度为 4 的数组。
- function countingSort(nums) {
- let arr = [];
- let max = Math.max(...nums);
- let min = Math.min(...nums);
- // 加上最小值的相反数来缩小数组范围
- let add = -min;
- for(let i=0, len=nums.length; i<len; i++) {
- let temp = nums[i];
- temp += add;
- arr[temp] = arr[temp] + 1 || 1;
- }
- let index = 0;
- for(let i=min; i<=max; i++) {
- let temp = arr[i+add];
- while(temp > 0) {
- nums[index++] = i;
- temp--;
- }
- }
- }
堆排序
根据数组建立一个堆(类似完全二叉树),每个结点的值都大于左右结点(***堆,通常用于升序),或小于左右结点(最小堆,通常用于降序)。对于升序排序,先构建***堆后,交换堆顶元素(表示***值)和堆底元素,每一次交换都能得到未有序序列的***值。重新调整***堆,再交换堆顶元素和堆底元素,重复 n-1 次后就能得到一个升序的数组。
***:O(n * logn),logn是调整***堆所花的时间。
最坏:O(n * logn)
平均:O(n * logn)
参考学习链接:
常见排序算法 - 堆排序 (Heap Sort)
图解排序算法(三)之堆排序
- function heapSort(nums) {
- // 调整***堆,使index的值大于左右节点
- function adjustHeap(nums, index, size) {
- // 交换后可能会破坏堆结构,需要循环使得每一个父节点都大于左右结点
- while(true) {
- let max = index;
- let left = index * 2 + 1; // 左节点
- let right = index * 2 + 2; // 右节点
- if(left < size && nums[max] < nums[left]) max = left;
- if(right < size && nums[max] < nums[right]) max = right;
- // 如果左右结点大于当前的结点则交换,并再循环一遍判断交换后的左右结点位置是否破坏了堆结构(比左右结点小了)
- if(index !== max) {
- [nums[index], nums[max]] = [nums[max], nums[index]];
- index = max;
- }
- else {
- break;
- }
- }
- }
- // 建立***堆
- function buildHeap(nums) {
- // 注意这里的头节点是从0开始的,所以***一个非叶子结点是 parseInt(nums.length/2)-1
- let start = parseInt(nums.length / 2) - 1;
- let size = nums.length;
- // 从***一个非叶子结点开始调整,直至堆顶。
- for(let i=start; i>=0; i--) {
- adjustHeap(nums, i, size);
- }
- }
- buildHeap(nums);
- // 循环n-1次,每次循环后交换堆顶元素和堆底元素并重新调整堆结构
- for(let i=nums.length-1; i>0; i--) {
- [nums[i], nums[0]] = [nums[0], nums[i]];
- adjustHeap(nums, 0, i);
- }
- }
希尔排序
通过某个增量 gap,将整个序列分给若干组,从后往前进行组内成员的比较和交换,随后逐步缩小增量至 1。希尔排序类似于插入排序,只是一开始向前移动的步数从 1 变成了 gap。
***:O(n * logn),步长不断二分。
最坏:O(n * logn)
平均:O(n * logn)
参考学习链接:
图解排序算法(二)之希尔排序
- function shellSort(nums) {
- let len = nums.length;
- // 初始步数
- let gap = parseInt(len / 2);
- // 逐渐缩小步数
- while(gap) {
- // 从第gap个元素开始遍历
- for(let i=gap; i<len; i++) {
- // 逐步其和前面其他的组成员进行比较和交换
- for(let j=i-gap; j>=0; j-=gap) {
- if(nums[j] > nums[j+gap]) {
- [nums[j], nums[j+gap]] = [nums[j+gap], nums[j]];
- }
- else {
- break;
- }
- }
- }
- gap = parseInt(gap / 2);
- }
- }
看完后如果大家有什么疑问或发现一些错误,可以在下方留言呀,或者在我的仓库里 提issues,我们一起讨论讨论😊