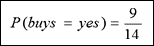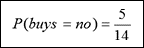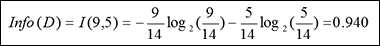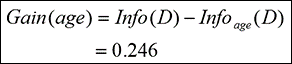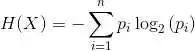【51CTO.com快译】众所周知,决策树在现实生活中有着许多实用的场景,它深刻地影响着包括分类和回归在内的、非常广泛的机器学习领域。可以说,在各种决策分析中,决策树能够起到直观且明确的决策辅助性作用。
什么是决策树?
决策树是一系列相关选择所产生的可能性结果的“展示图”。它允许个人或组织根据其成本、概率和效益,来对各种可能采取的行动进行权衡。
顾名思义,决策树使用的是树状的决策模型。它既可以被用于推进各种非正式的讨论,又可以被用来通过“绘制”算法,以预测那些在数学上的***选择。
决策树通常是从单个节点开始的。该节点可以分支出各种可能性的结果。同时,这些结果都会导致新的节点产生,而这些节点则会继续分枝出另一些其他类型的可能性。因此,这些最终形成一个树状的结构。
在决策树中一般有三种不同类型的节点:机会节点、决策节点和末端节点(end node)。我们用圆形来表示的机会节点,代表某些结果的概率;用正方形来表示的决策节点,代表要做出的各种决策;结束节点表示某个决策路径的最终结果。
决策树的优缺点
优势
- 决策树能够生成各种可理解的规则。
- 无需大量计算,决策树即可执行分类。
- 决策树能够处理连续变量和分类变量。
- 决策树能够清楚地表明哪些字段对于预测或分类是最为重要的。
缺点
- 决策树不太适合于那些目标为预测连续属性值的估算类任务。
- 在面对有着多个类、和相对较少的训练样本的分类问题时,决策树容易出现错误。
- 在训练的过程中,决策树在计算成本上的开销比较高。在每个节点上,我们必须先对每个候选字段进行排序,然后才能找到其***的拆分方式。某些算法会使用字段的组合,以对***组合的权重进行搜索。另外,由于必须形成和比较各种候选子树,因此修剪算法(Pruning algorithms,https://www.edureka.co/blog/implementation-of-decision-tree/)的开销会更大。
创建决策树
让我们考虑一个场景,有一组天文学家发现了一颗新的行星,他们感兴趣的问题是:它是否可能是下一个地球呢?
显然,在做出明智的判断之前,我们值得深入研究的决定性因素有许多,包括:该星球上是否存在着水、温度是多少、地表是否容易持续遭受暴风雨的影响、动植物是否在此类特定的气候中能生存活下来等方面。
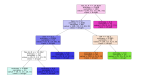
下面,让我们通过创建一个决策树,来判定它是否人类下一个“栖息地”。
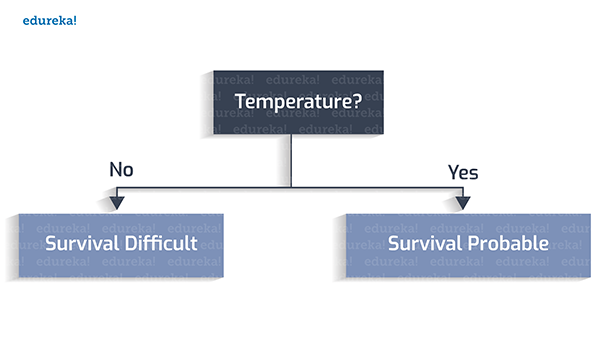
首先,我们设定宜居的温度在0到100摄氏度之间。
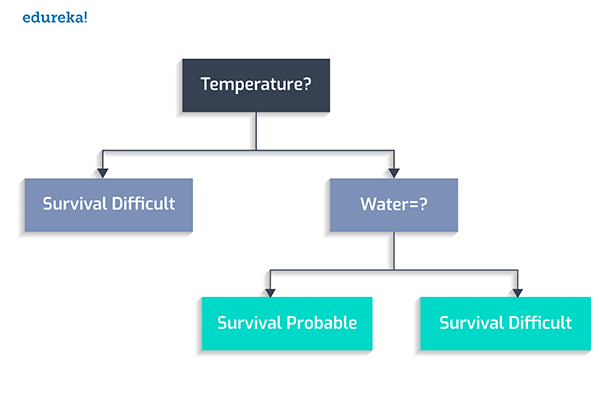
其次,是否存在着水?
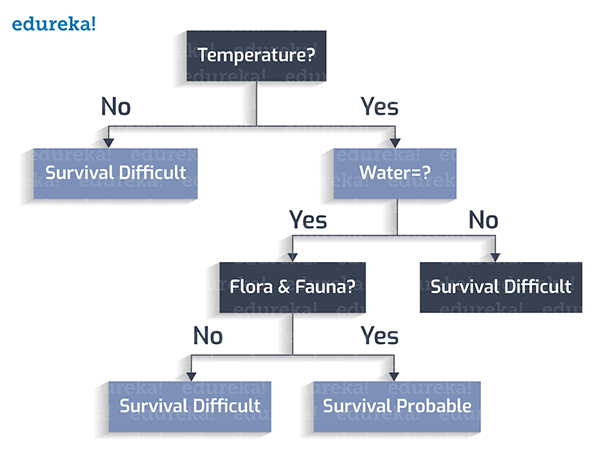
然后,动植物是否繁茂?
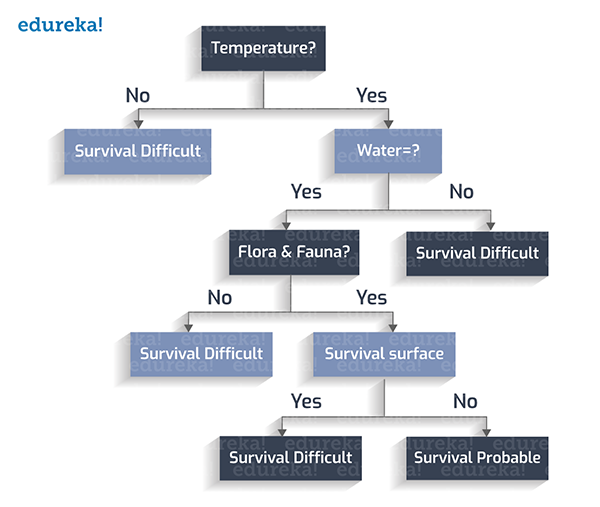
组后,该星球的表面是否有风暴?
至此,我们就得到了一个完整的决策树。
分类规则
分类规则是:在考虑了所有的可能性之后,为每种方案分配一个类变量(class variable)的状况。
类变量
我们为每一个叶节点都分配一个类变量。类变量将直接影响我们判断的最终输出。
下面让我们从上面创建的决策树中,推导出如下的分类规则:
1. 如果温度不在273至373K(开尔文,热力学单位)之间,则视为:生存困难。
2. 如果温度在273至373K之间,且不存在水,则视为:生存困难。
3. 如果温度在273至373K之间,存在水,但没有动植物,则视为:生存困难。
4. 如果温度在273至373K之间,存在水,存在动植物,且无地表暴风雨,则视为:生存可能。
5. 如果温度在273至373K之间,存在水,存在动植物,但存在地表暴风雨,则视为:生存困难。
决策树
本例的决策树由如下部分组成:
- 根节点:在上例中,“温度”因素被视为根。
- 内部节点:具有一个传入边(incoming edge)和两到多个传出边(outgoing edge)的节点。
- 叶子节点:不再具有传出边的末端节点。
根据上述三个部分,我们从根节点开始,逐个检查测试条件(test condition),并将判断结果(或称控制)分配给其中一个传出边,以便将其作为另一个节点的传入边,进行下一轮条件测试。当所有测试条件都遍历完毕并到达叶子节点时,该决策树完毕。而叶子节点则包含了是否认可该决策(判断)的各种类标签(class labels)。
您一定有些疑惑:为什么我们会将“温度”属性作为根,来构造决策树呢?如果选择其他属性,将有什么不同呢?的确,不同的属性特征会创建出许多不同的树。我们需要通过遵循某种算法来选择***的决策树。下面我们来讨论一种被称为“贪婪法则(Greedy Approach)”的决策树创建算法。
贪婪法则
根据维基百科,贪婪法则是基于启发式问题解决(Heuristic Problem Solving)的概念,在每个节点上做出***的局部选择。然后通过这些局部的***选择,在全局范围内找到了近似的***解。
该算法包括:
1. 在每个阶段(节点),选择出***特征作为测试条件。
2. 接着将节点拆分为各种可能性的输出(内部节点)。
3. 重复上述步骤,直到所有测试条件都在叶子节点中被遍历到。
我们回到刚才的问题:如何选择初始的测试条件呢?这里会涉及到两个概念:熵(Entropy)和信息增益(Information Gain)。
熵:在决策树中,熵表示同质性。如果数据是完全均匀的,则熵为0;否则,如果数据被分割了(如50比50%),那么熵为1。
信息增益:信息增益表示节点被拆分时,其熵值的增与减。
我们的目的是,让被选取进行拆分的属性特征具有***的信息增益。因此,根据熵和信息增益的计算值,我们需要在任何特定步骤中,选取***的属性。
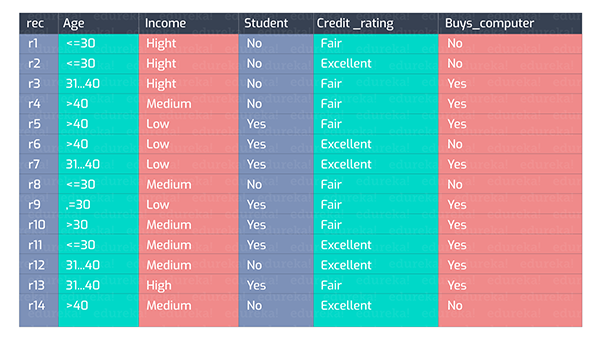
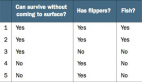
我们来看下图的一组数据:
我们可以根据上图中各种维度的属性特征集合,得出一系列不同种类的决策树。下面 是两种创建试验:
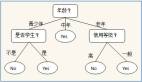
树的创建试验 1:
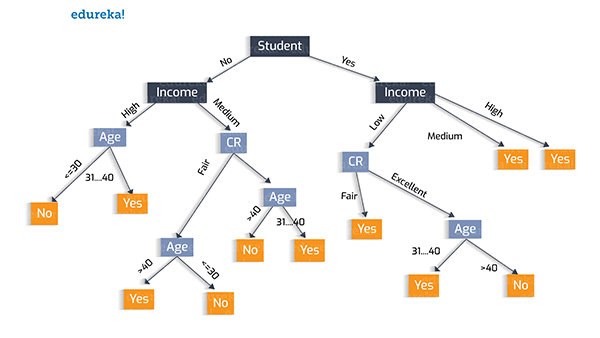
在此,我们使用“学生”,这一属性特征作为初始化的测试条件,其决策树如下图所示。
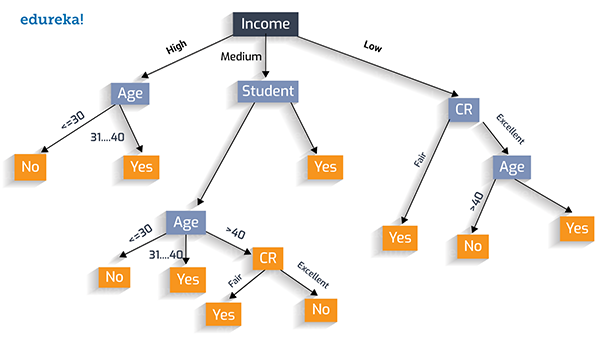
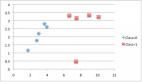
树的创建试验 2:
同样,我们可以选择“收入”作为测试条件,如下图所示:
用贪婪法则创建***的决策树
在此,我们涉及到两个类:“Yes”表示此人会购买电脑;“No”表示不购买。为了计算熵和信息增益,我们来看看这两个类分别的概率值。
»Positive:“buys_computer=yes”的概率为:
»Negative:“buys_computer=no”的概率为:
D的熵:我们将概率值放入上面的公式,以求出熵。
在准备阶段,我们预先对熵的值进行了分类,它们分别为:
熵 = 0:数据完全是同质的 (纯)
熵 = 1:数据被分为50%比50% (不纯)
由于我们算出的熵值是0.940,可见是不纯的。
下面让我们通过深入研究,来找出合适的属性特征,以计算信息增益。
如果我们在“年龄”上进行拆分,那么就能够按照年龄的不同阶段,来区分是否购买电脑产品。
例如,对于年龄在30岁及以下的人来说,有2人购买(Yes),3人不购买(No)电脑。那么我们针对三个年龄阶段(将年龄属性特征值进行拆分)的人,计算出针对***一列(是否购买电脑)的Info(D)。
可见,信息增益便是总的Info(0.940)与以年龄为属性计算的Info(0.694)的差。
因此,这就是我们如果使用“年龄”为属性进行拆分的因子。同理,我们也可以计算出其余属性特征维度的“信息增益”,如:
信息增益 (年龄) = 0.246
信息增益 (收入) = 0.029
信息增益 (学生) = 0.151
信息增益 (信用评级) = 0.048
通过对上述值的综合比较,我们不难发现:“年龄”的“信息增益”***,因此,拆分“年龄”是一个比较好的决策。
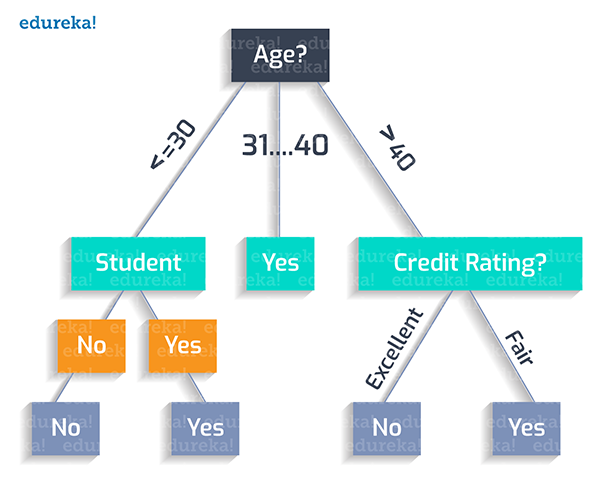
可见,我们应该创建的***决策树应该如下图所示:
由上图可见,我们应该按照如下逻辑“绘制”出该决策树的分类规则:
如果某人的年龄小于30岁,而且他不是学生,那么他就不会买产品。
Age (<30) ^ student(no) = NO
如果某人的年龄小于30岁,并且他是学生,那么他就会购买该产品。
Age (<30) ^ student(yes) = YES
如果某人的年龄在31岁至40岁之间,那么他最有可能购买产品。
Age (31…40) = YES
如果某人的年龄超过了40岁,且信用评级非常好,那么他就不会买产品。
Age (>40) ^ credit_rating(excellent) = NO
如果某人的年龄超过了40岁,且信用评级尚可,那么他很可能会购买产品。
Age (>40) ^ credit_rating(fair) = Yes
这便是我们根据上例所实现的***决策树。
原文标题:How to Create a Perfect Decision Tree,作者:Upasana Priyadarshiny
【51CTO译稿,合作站点转载请注明原文译者和出处为51CTO.com】