磁盘并不是万无一失的,也可能发生故障和损坏。磁盘发生故障是灾难性的,存储介质的损坏如果在没备份的情况下,基本是100%丢失数据,比rm -rf 还严重,那么磁盘的故障有那么些?
- 间歇性故障
- 介质损坏
- 写故障
- 磁盘崩溃
在这些故障的时候有哪些应对策略和办法?我们这章来来学习一下。
间歇性故障
当我们尝试从磁盘读一个块的时候,可能这个块的内容未正确的发送到磁盘控制器,这就是一次间歇性的故障,控制器会以一种办法来判断这个磁盘块的好坏,如果读的数据是坏的,控制器会尝试再次读取发起请求,直到读取的数据正确位置,或者发送N次请求,然后再停止。
同样,我们尝试写入一个扇区,可能写入的内容不是原本想要写入的内容,唯一的办法就是磁盘把写入的内容读取出来跟磁盘控制器的内容再比较一下。然而,跟磁盘控制器比较,其实还可以读取写入的扇区,并且查看状态是否为"好",如果状态是"坏"那么就重写,这个状态如何产生的呢?这就引出了是checksum概念。
校验和(checksum)
在说checksum之前,我们来玩个小游戏:
桌子上摆放了7个黑白棋子,魔术师蒙着眼睛看不见棋子。魔术师徒弟在看完7个棋子之后在右边添加个棋子,和其他棋子并排,这个时候有8个棋子,魔术师依旧蒙着眼睛。这个时候观众可将其中的一个棋子翻转,或者不翻转任何一枚。观众和徒弟一言不发,魔术师并不知道观众是否翻转棋子。
现在魔术师摘下眼罩,观察8枚棋子,然后可以说出是否翻转了棋子,识破观众的行为。那么魔术师是如何识破的呢?
校验和:在磁盘的每个扇区都有几个附加位,这个被称为校验和。在数据读取的时候,如果校验和跟数据位不符合,那么就判断读取错误。不过校验和正确,也有可能数据是错误的,这个的可能性跟校验位的长度成负相关。校验位越长,判断错误的概率越小。
校验和是基于扇区内所有位的奇偶性(parity),如果二进制的集合中有奇数个1,那么数据位有奇数奇偶性并增加值为1的奇偶位。同理,如果有偶数个1,那么数据位有偶数奇偶性并且增加值为0的奇数位。
假如我们用一个字节(8bits)来判断奇偶,并且检测出错误的可能性为50%,那么出错的概率为,1/2^8,如果用4个字节呢,则出错率为1/2^32。相对于40亿次中只有一次错误没被检测出来。
一般的在数据库中用的是CRC或者是FNV算来进行checksum的,在PostgreSQL中用得上 FNV-1a,我们来看看PG是如何实现的。
PostgreSQL-CheckSum
Postgres默认是不开启checksum的,在初始化数据库的时候可以通过选项-k开启。
- -k, --data-checksums use data page checksums
使用的算法是FNV-1a,下面的地址是这个算法的详细介绍:http://www.isthe.com/chongo/tech/comp/fnv/
核心代码在:src/include/storage/checksum_impl.h
函数入口:pg_checksum_block
官方描述:
PG的实现跟官方的实现有区别,官方的实现为:
而PG在乘之前,先右移了17位,然后再xor。
计算出来的结果都存储在页头PageHeaderData->pd_checksum
数据从shared_buffer刷盘以及从disk读取block都需要计算checksum。如果只是在内存中变更数据页,是不需要计算checksum的。
感兴趣的可以gdb跟一下看看。
再回到上面的小游戏,魔术师只要跟徒弟在之前协定好,有偶数个白或者黑,问题就解决了,这也是一种奇偶校验的实现。
介质损坏
磁盘也是有使用寿命的,当磁盘损坏后,破坏是物理性的,数据是不可能完全的恢复回来。在上面我们介绍了如何来高效的检测介质的故障或读写的故障,但是却没说明如何解决这个问题。
在磁盘的扇区损坏的问题上,可以用2块或者多块磁盘来存储数据。例如我们写入内容X,通常扇区是成对的,我们把写入X的扇区称作为(左拷贝)Xl和(右拷贝)Xr。读函数可以读取Xl或者Xr,返回一个结果w,那么w是X的真实的内容。前提是我们通过CheckSum对Xl和Xr扇区的完整性做了排查。(这段内容有点绕口,其实就是写2份数据到不同的磁盘扇区,然后可以任意从其中一个读取到你想要的内容)。
写的策略也是一样的,例如写入Xl,检查是否返回状态为"好",如果不是,就需要不停的写,到达若干次后,如果任然未成功,则可表示该扇区是坏的,则可以用Xr来替换损坏Xl。相反对Xr跟Xl是一样的逻辑,重复Xl的动作即可。
读策略是交互的,交替的读取Xl和Xr,预先设定个很大的数字,若尝试超过这个数据,则可以确定X是无法读取的。
RAID
上面讨论的内容其实就是RAID(Redundant Array of Independent Disk,独立磁盘冗余阵列)。磁盘崩溃发生率一般由平均失效时间来衡量,假设磁盘平均失效时间为10年,则每年磁盘中的1/10会发生故障,为了避免这种故障,就采用了这种策略,当一个数据盘或者冗余盘发生崩溃的时候,其他的磁盘可用于恢复故障磁盘,从而使得没有任何数据会丢失。RAID分了很多等级,我们下面就看看不同等级的计算和使用。
RAID-1
RAID-1方案使用2块磁盘做扇区的拷贝,一个做数据盘,一个做冗余盘,或者互换。相当于有2份磁盘空间来存储数据(空间浪费),任何一份失效,可以使用未损坏的进行修复,除非2块盘同时失效。
看个例子:假设每个磁盘的使用寿命为10年,那么意味着每年的损坏率为10%。如果磁盘被镜像,发生故障的时候我们可以利用另外一块好的替换他。所以造成错误的至少要2个磁盘的数据都丢失,才能说是数据无法恢复。假设替换的时间为3个小时,这是一天中的1/8,或者是1年的1/2920,那么10年的故障率为1/29200,2块磁盘之一平均5年发生一次故障,那么丢失数据的概率大概为5*29200=14600年。
RAID-4(奇偶块)
RAID是以磁盘块为奇偶校验,假设有N块数据盘,一个冗余盘,在冗余盘中,第i块由所有的数据盘的第i块奇偶校验位组成,也就是说,所有第i块盘的j位,包括数据盘和冗余盘,他们中间必须有偶数个1,而我们总是选取冗余盘的位让条件为真。
假设我们有4块盘,3个数据盘,一个冗余盘。假设一个块只有一个字节,8位。
盘1:11110000
盘2:10101010
盘3:00111000
冗余盘
盘4:01100010
在1,2,4,5,7位有两个1,在3,4有4个1,在6和8有零个1。
利用冗余盘的位让数据盘的奇偶校验条件为真。
读:
从任意一个数据盘读取是没有任何差别。
写
当我们写一个数据盘的一个新块,我们不仅仅需要改变那个数据块,还需要改变冗余盘的相应的块,以保持数据盘的奇偶性。一个朴素的办法是读取N个数据盘的相应块,取他们的摸2和,并重写冗余盘,那么这样就会是N+1次的磁盘I/O。
还有个更好的办法,只关注在被写盘的i块的老版本和新版本,操作如下:
1、读要要被改变的数据盘的旧值
2、读冗余盘的相应块
3、写新数据盘
4、重新计算并写冗余盘的块
这样就只有4次I/O操作
摸2代数解释
假设有如下三个数据盘,***个块如下:
盘1:11110000
盘2:10101010
盘3:00111000
冗余盘:01100010
假设盘2的块由10101010改变为11001100,我们来求盘2上的旧值和新值的摸2和,得到
01100110,这个结果告诉我们,必须改变冗余盘的***块的位置,2,3,6,7的值。那么冗余盘为:0000100,如下:
盘1:11110000
盘2:11001100
盘3:00111000
冗余盘:0000100
这样每列依旧有偶数个1
故障恢复
如果是冗余盘坏了,直接换一块新盘,并且重新计算奇偶。如果是数据盘坏了,也是换一个新盘,不起根据其他盘重新计算它的数据。我们来看个例子:
盘1:11110000
盘2:????????
盘3:00111000
盘4:01100010
我们取每一列的模2和,可以推导出盘2为:
盘1:11110000
xor
盘2:00111000
=:11001000
xor
01100010
=10101010
RAID-5
在RAID-4的策略中,除非2块盘同时损坏,否则还是能有效的保护数据。不过有个缺点,就是无论是读和写都需要访问冗余盘。从上面故障恢复的例子可以发现,恢复数据盘和冗余盘是一样的策略,都是取其它盘的模2和。这样,我们就不必要把一个盘做冗余盘,而把其他盘作为数据盘,相反,我们可以把每个磁盘作为某写块的冗余盘来处理,这种改进称为RAID-5。
假设我们有4块盘,0-3。***个盘编号为0,讲作为编号为4,8,12等盘的冗余,因为当被4除时,余数为0。编号为1的盘将作为编号为1,5,9等块的冗余。盘2是2,6,10块的冗余,盘3是3,7,11等块的冗余。
如果每个盘读写负荷一样,如果所有的块有相同的可能性被写,那么对于一次写,每个盘有1/4的机会,并且还有1/3的机会作为那个块的冗余盘。这样,4个盘的每个涉及写的机会是1/4+3/4*1/3=1/2
多个盘的崩溃处理(RAID-6)
前面讲的都是一块盘的崩溃,如果涉及到多个盘的崩溃,还是无法处理的。多个盘的崩溃有一个纠错码原理,允许我们处理多个盘的崩溃,前提的我们有足够多的冗余盘。这个 策略导致了***的RAID级别-RAID-6。这个策略是基于海明码(Hamming code)进行纠错的。
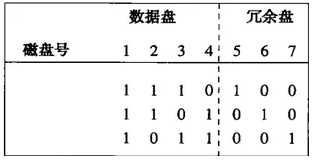
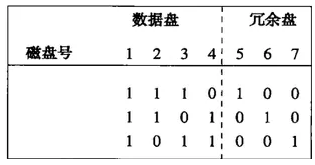
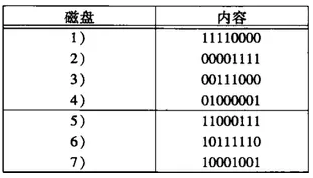
我们来看个例子,一个7个磁盘的系统,磁盘编号为1-7,前面4个是数据盘,5-7是冗余盘。数据盘和冗余盘组成的一个3*7的矩阵,如下图:
如图,请注意:
1、除了全0列之外的,三个0和1的所有可能的列都在这个矩阵中
2、冗余盘有单个1
3、数据盘至少各有两个1
通过这个矩阵可以知道:
1、盘5是盘1、2、3相应位的摸2和
2、盘6是盘1、2、4相应位的模2和
3、盘7是盘1、3、4相应位的模2和
通过这个规则,我们就能从两个同时发生故障的磁盘崩溃中恢复。
读
我们从任何一个数据盘读取数据,不用理睬冗余盘
写
写的话就需要考虑冗余盘。为了写某个块,需要计算新旧块的摸2和,这些位以模2和的方式加入到满足条件的所有冗余盘相应块中。
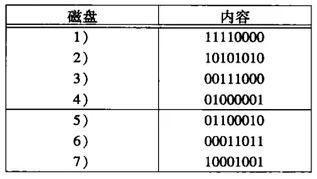
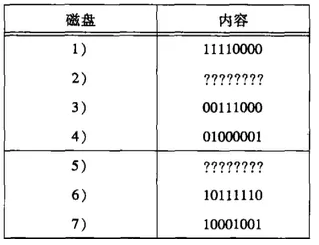
看个例子:
我们把第二个盘修改为00001111,新值和旧值的模2和为:10100101,因为盘5和6在盘行1和行2都有1
所以我们需要拿他们的***个块跟刚才算出来的值10100101执行摸2和,也就是说我们需要对这2个块的1,3,6,8位置求反。
盘5:
10100101
xor
01100010
=
11000111
盘6:
10100101
xor
00011011
=
10111110
所以结果如下:
RAID-6故障恢复
假设故障盘为a和b,我们可以从下面这个矩阵中能够把a和b的列不同的某个行r找到,假设a是0,而b是1.
然后我们通过取来自b之外所有的行r有1的磁盘相应位模2,我们就能计算出b。计算完b,我们必须用所有其他的盘重新计算a。办法是取该行带1的那些其他磁盘的位摸2.
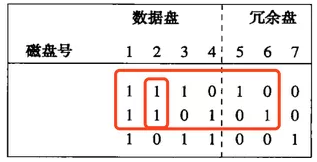
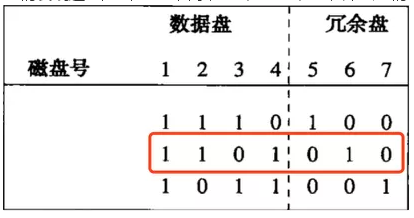
看个例子,如果盘2和盘5在同一时间损坏,如下图:
我们发现这2个盘在列2不同,盘2是1盘5是0,那么我们用盘1,4,6来恢复盘2如下图:
盘2通过计算得到:
盘1:11110000
xor
盘4:01000001
=10110001
Xor
盘6:10111110
=00001111
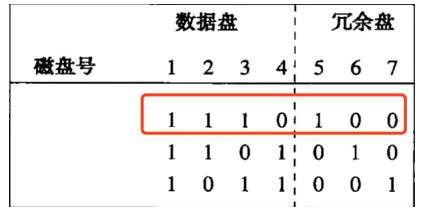
盘5可以用盘1,2,3来恢复,如下图:
盘1:11110000
xor
盘2:00001111
=11111111
xor
盘3:00111000
=11000111
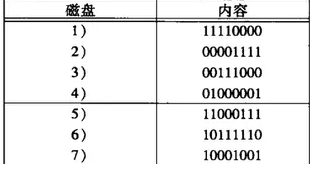
这样盘2和盘5都恢复了,结果如下:
关于RAID-6,磁盘的数量可以是任意次方-1,例如2^k-1,k是冗余盘,剩下的2^k-k-1是数据盘,所有冗余盘差不多是数据盘的对数增长的,并且都可以构造成矩阵来表示。
书中只大概介绍了这几种RAID,不过现在有跟多的RAID,例如:
- RAID-0:Data Stripping
- RAID-1:磁盘镜像
- RAID-0+1:RAID-0和RAID-1的结合体
- RAID-2:带海明吗校验
- RAID-3:带奇偶校验并行传送
- RAID-4:带奇偶校验独立磁盘结构
- RAID-5:分布式奇偶校验
- RAID-6:带2种分布式存储奇偶校验
- RAID-7:优化的高速传输磁盘结构
- RAID-10:高可靠和高效磁盘结构
- RAID-53:高速数据传输磁盘结构
总结:主要是讲磁盘的损坏和恢复方面的内容,包括如何检测损坏和如何恢复,checksum是个很好的检测手段,而磁盘的冗余是在存储介质损坏的时候提供有力的数据保护,并且分析了几种冗余策略。下一章我们来看看数据是如何在磁盘组织的,包括定长&变长数据的存储,Tuple的修改(插入,删除,跟新),跨块的存储和列存储相关内容,并且我们用C语言自己来写个例子程序。