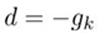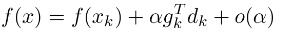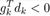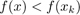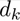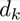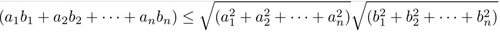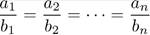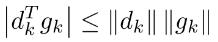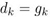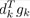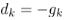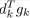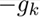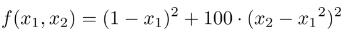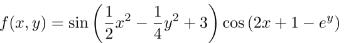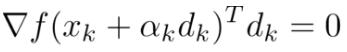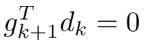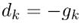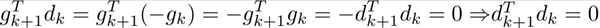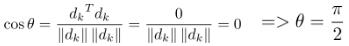当今世界，深度学习应用已经渗透到了我们生活的方方面面，深度学习技术背后的核心问题是最优化(Optimization)。最优化是应用数学的一个分支，它是研究在给定约束之下如何寻求某些因素(的量)，以使某一(或某些)指标达到最优的一些学科的总称。
梯度下降法(Gradient descent，又称最速下降法/Steepest descent)，是无约束最优化领域中历史最悠久、最简单的算法，单独就这种算法来看，属于早就“过时”了的一种算法。但是，它的理念是其他某些算法的组成部分，或者说在其他某些算法中，也有梯度下降法的“影子”。例如，各种深度学习库都会使用SGD(Stochastic Gradient Descent，随机梯度下降)或变种作为其优化算法。
今天我们就再来回顾一下梯度下降法的基础知识。
1. 名字释义
在很多机器学习算法中，我们通常会通过多轮的迭代计算，最小化一个损失函数(loss function)的值，这个损失函数，对应到最优化里就是所谓的“目标函数”。
在寻找最优解的过程中，梯度下降法只使用目标函数的一阶导数信息——从“梯度”这个名字也可见一斑。并且它的本意是取目标函数值“最快下降”的方向作为搜索方向，这也是“最速下降”这个名字的来源。
于是自然而然地，我们就想知道一个问题的答案：沿什么方向，目标函数 f(x) 的值下降最快呢?
2. 函数值下降最快的方向是什么
先说结论：沿负梯度方向
函数值下降最快。此处，我们用 d 表示方向(direction)，用 g 表示梯度(gradient)。
下面就来推导一下。
将目标函数 f(x) 在点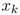
处泰勒展开(在最优化领域，这是一个常用的手段)：
高阶无穷小 o(α)可忽略，由于我们定义了步长α>0(在ML领域，步长就是平常所说的learning rate)，
因此，当
时
即函数值是下降的。
此时
就是一个下降方向。
但是
具体等于什么的时候，可使目标函数值下降最快呢?
数学上，有一个非常著名的不等式：Cauchy-Schwartz不等式(柯西-许瓦兹不等式)①，它是一个在很多场合都用得上的不等式：
当且仅当：
时等号成立。
由Cauchy-Schwartz不等式可知：
当且仅当
时，等号成立，
最大(>0)。
所以，
时
最小(<0)，f(x) 下降量最大。
所以，
是最快速下降方向。
3. 缺点
它真的如它的名字所描述的，是“最快速”的吗?从很多经典的最优化书籍你会了解到：并不是。
事实上，它只在局部范围内具有“最速”性质；对整体求最优解的过程而言，它让目标函数值下降非常缓慢。
4. 感受一下它是如何“慢”的
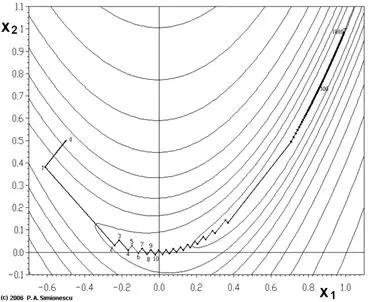
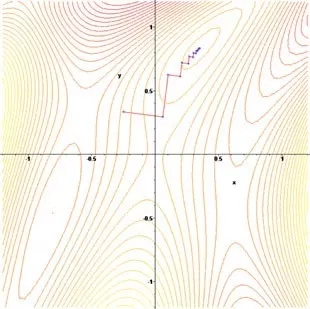
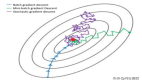
先来看一幅图②
这幅图表示的是对一个目标函数寻找最优解的过程，图中锯齿状的路线就是寻优路线在二维平面上的投影。从这幅图我们可以看到，锯齿一开始比较大(跨越的距离比较大)，后来越来越小；这就像一个人走路迈的步子，一开始大，后来步子越迈越小。
这个函数的表达式是这样的：
它叫做Rosenbrock function(罗森布罗克函数)③，是个非凸函数，在最优化领域，它可以用作一个最优化算法的performance test函数。这个函数还有一个更好记也更滑稽的名字：banana function(香蕉函数)。
我们来看一看它在三维空间中的图形：
它的全局最优点位于一个长长的、狭窄的、抛物线形状的、扁平的“山谷”中。
找到“山谷”并不难，难的是收敛到全局最优解(在 (1,1) 处)。
正所谓：
| 世界上最遥远的距离，不是你离我千山万水，而是你就在我眼前，我却要跨越千万步，才能找到你。 |
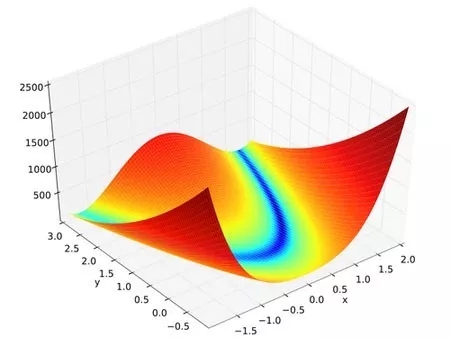
我们再来看下面这个目标函数的寻优过程④：
和前面的Rosenbrock function一样，它的寻优过程也是“锯齿状”的。
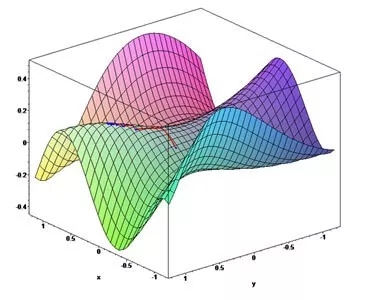
它在三维空间中的图形是这样的：
总而言之就是：当目标函数的等值线接近于圆(球)时，下降较快；等值线类似于扁长的椭球时，一开始快，后来很慢。
5. 为什么“慢”?
从上面花花绿绿的图，我们看到了寻找最优解的过程有多么“艰辛”，但不能光看热闹，还要分析一下原因。
在最优化算法中，精确的line search满足一个一阶必要条件，即：梯度与方向的点积为零
(当前点在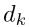
方向上移动到的那一点
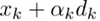处的梯度，与当前点的搜索方向
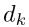的点积为零)。
由此得知：
即：
故由梯度下降法的
得：
即：相邻两次的搜索方向是相互直交的(投影到二维平面上，就是锯齿形状了)。
如果你非要问，为什么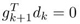
就表明这两个向量是相互直交的?那是因为，由两向量夹角的公式：
可知两向量夹角为90度，因此它们直交。
6. 优点
这个被我们说得一无是处的方法真的就那么糟糕吗?
其实它还是有优点的：程序简单，计算量小；并且对初始点没有特别的要求;此外，许多算法的初始/再开始方向都是最速下降方向(即负梯度方向)。
7. 收敛性及收敛速度
梯度下降法具有整体收敛性——对初始点没有特殊要求。
采用精确的line search的梯度下降法的收敛速度：线性。
引用：
- https://en.wikipedia.org/wiki/Cauchy%E2%80%93Schwarz_inequality
- https://en.wikipedia.org/wiki/Gradient_descent
- https://en.wikipedia.org/wiki/Rosenbrock_function
- https://en.wikipedia.org/wiki/Gradient_descent
【本文是51CTO专栏机构360技术的原创文章，微信公众号“360技术（ id: qihoo_tech）”】
