春招来袭啦!又要面试啦!
程序员面试展示什么最重要?当时是你渊博的计算机学识,以及聪明的小脑瓜。
如果你学富五车,上知深度学习, 下知财务会计,那短短数小时也绝不够你表演。所以,你一定得知晓面试官的套路,随口丢出几个应景的“冷知识”卖个乖巧。
如果你基础不行,三天前刚准备转码,那就更得准备几个的小把戏,不用打肿脸也能充一回胖子。
基于这两个需求,今天文摘菌就来给大家介绍三个讨巧的数据结构。面试当中一提,那可是相当撑场面。
这三个数据结构就是。登登登等…
1. 布隆过滤器(bloom filter)
2. 前缀树(prefix trie)
3. 环形缓冲(ring buffer)
先来说一下,为什么挑了这三个数据结构。
首先我觉得,你提到的数据结构要稍微冷门一些,这样别人就会认为你了解很多不同类型的数据结构。但它不能太冷门,以免你的面试官要求你真正解释实现细节或原理,那时你就game over了。***是你提到的数据结构有点冷门,但你的面试官听说过,对它有印象。
面试官都希望自己什么都知道,他们听说过这种数据结构但又不太了解,当你向他们介绍时,他们就会觉得你懂得特别多。
除此之外,这些数据结构还应该具有实际用例,以便在技术面试的时候,你能有机会展开介绍。它虽然稍微有点冷门但也不能太low,你如果只知道一些菜鸡水平的数据结构(比如双向链表),你的面试八成就凉了。
所以,这三个数据结构就被***选中啦!
布隆过滤器
布隆过滤器是集合的概率版本。检测集合是否包含某元素的时间复杂度为O(1)、空间复杂度为O(N)。Bloom过滤器也可以检测出集合是否可能包含该元素,它的时间复杂度为O(1),而空间复杂度只需要O(1)!
谁会真正使用布隆过滤器?
Chrome需要在不牺牲速度或空间的情况下保护你免受访问垃圾邮件网站。
想象一下,如果每次你点击一个链接,Chrome都必须进行网络通话来检查它庞大的垃圾邮件URL数据库,然后才允许你访问这个页面,这会不会让你等疯掉。此外,设想一下,如果Chrome改善延迟的解决方案是在本地存储整个垃圾邮件URL列表,这根本就是不可行的!
所以,chrome在本地存储了一个潜在垃圾邮件URL的布隆过滤器,这既节省时间又节省空间,可以快速检查给定的URL是否为垃圾邮件。对于普通的URL,布隆过滤器对“非垃圾邮件”的响应就足够判定了。如果一个URL被标记为“可能是垃圾邮件”,那么Google可以在跳转之前检查它真实数据库。事实证明,当你愿意牺牲绝对时,你可以做出伟大的事情!
布隆过滤器的原理
布隆过滤器的维基百科页用大量的术语描述了实现细节,所以在这里我会用简单的描述一下实现过程。如果你想要更精确的细节,你应该去看看维基百科。我会略过很多步骤,但我会让你有一个大致了解。
如果你想在Bloom过滤器中插入一个元素,首先假设有N个不同的确定性哈希函数。当同一个元素输入不同哈希函数时,会得到不同的值(冲突是可以有的)。
使用每个哈希函数的输出作为数组的索引[注释1,注释2],并对应每个索引i将数组[i]设置为true。插入元素就完成了!插入元素的时间复杂度是O(1),因为对每个插入元素所做的唯一工作是运行恒定数量的哈希函数,并设置恒定数量的数组索引。
那该如何检查布隆过滤器是否包含该元素? 再次运行所有相同的哈希函数!
哈希函数是确定性的,因此相同的输入应返回相同的输出。所以相对应每个索引,检查布隆过滤器的数组是否在该索引处设置为true即可。如果哈希函数输出的数组的每个单元都为真,那么可以很高的概率说这个元素已经插入到了布隆过滤器中。这一方法总是存在误报的可能性。不过,布隆过滤器的一大特色是永远不会出现漏报。
那么,你需要多少个哈希函数,又需要多大的数组呢?这你就得好好算一番了。维基百科对它们的解释更详细,你值得一读。
注释1:如何使用哈希函数的输出作为索引:设哈希函数输出整数值M,取长度N。N%M(N mod M)得到一个值Q,即0≤Q
注释2:实际上,你应该使用位数组而不是普通数组。数组的每个元素至少需要1个字节,而你只需要为“数组”的每个元素存储true / false。因此,你可以通过将其存储为位数组来节省空间,这是这个数据结构的重点。如果你想要听起来很聪明,那么位数组(也就是位向量)也值得你在面试时提出。嗯,真正的面试专家建议总是在脚注中。
注释3:严格来说,如果你的所有哈希函数都在O(1)时间内运行,那么插入的复杂度才是O(1)。
前缀树(prefix trie)
前缀树是一种数据结构,允许你通过其前缀快速查找字符串,还可以查找有公共前缀的字符串。
我对介绍这一数据结构的***条建议是,将它称为“前缀树”,而不仅仅是“树”。这样,你就让面试官知道你是那种了解与前缀和后缀相关算法的人,并且你也希望对你的fancy数据结构进行准确描述。后缀树也是一个非常有趣的话题,但实现细节十分残暴。这就是为什么我只是谈论前缀树,并且假装了解后缀树。
谁会真的用前缀树?
基因组学研究人员!
事实证明,现代基因组研究在很大程度上依赖于字符串算法和数据结构,因为你试图从组成基因组序列的数百万个核苷酸中探索奥秘。对于基因组数据,你经常需要对齐序列,找到差异或找到重复的模式。如果你想了解更多相关信息,可以先阅读生物信息学读物,然后参与“DNA测序算法”或“生物信息学算法”等课程。
如果你想要阅读一些真正有意思的读物,我强烈建议你读一读药物基因组学。随着基因组测序和字符串算法的进步,我们实际上可以预测使用个体的基因组,来确定它们是否具有对药物正确反应的正确基因。例如,如果他们的基因组缺少用于产生处理某种药物的酶的基因,那么药物可能会对他们产生副作用。如果我们知道什么基因是重要的,我们可以给他们一种不同的药物!
我承认,前缀树和基因组学之间的联系不太紧密。其实前缀树的最直接用法就是用来查字典啦!但光这么讲不是忒无聊了点么。
前缀树的原理
想象一下,你有一棵树,每个节点都有一个包含26个子节点的数组,每个子节点对应一个英文字母。(如果要包含其他字符,可以将26更改为不同的值。)要在你的树中表示单词,你将从根节点开始,沿着路径向下走,并在每个节点添加一个字母。
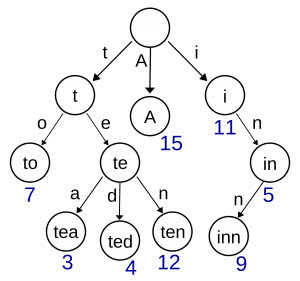
例如(图片来源维基百科),对于“tea”这个词,你从根开始,被引导到t节点,然后是e,***是a。因此,搜索单词需要O(N)的时间(其中N是单词的长度),如果单词的前缀不存在,则可以提前结束。如果我查询“zzzzzzzz”,树可以在“zz”之后结束查询。
环形缓冲区(ring buffer)
环形缓冲区是使用普通数组的一种非常好的方式,它主要被用于处理数据流。
谁会真的使用环形缓冲区?
说不定Netflix会用?
我用google搜索“netflix ring buffer”,发现了他们发布了一些开源环缓冲区代码。但问题是,公司真的会用他们已经开源的代码嘛?
环形缓冲区的原理
好啦好啦。真的还有人在读这篇文章嘛。
如果你读到了这儿,说明你基础一定还不错,那就直接去维基百科瞅一眼这个数据结构吧,比前两个简单多了!
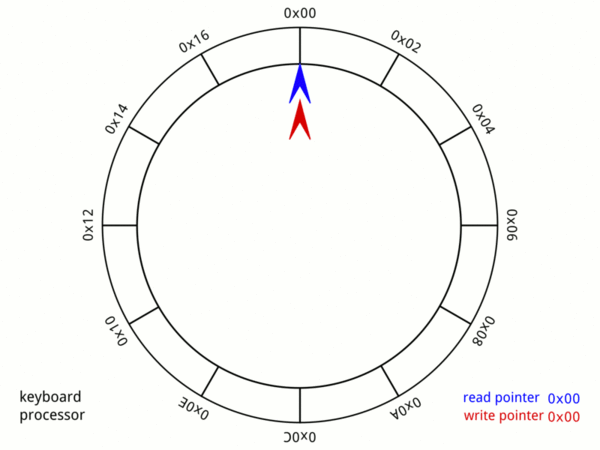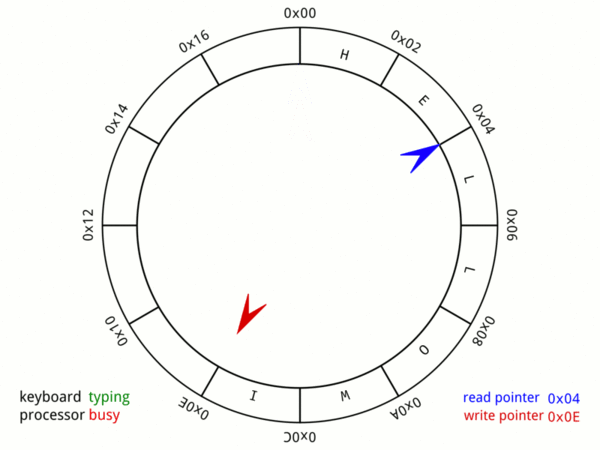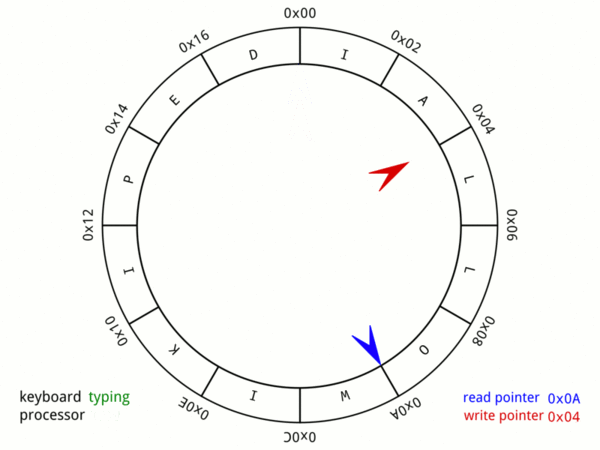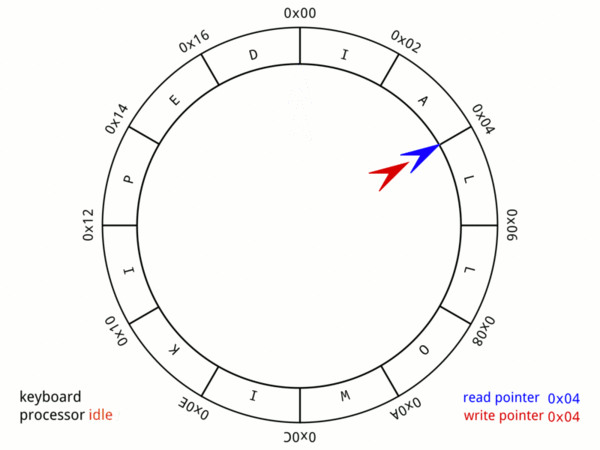
总结一下,今天文摘菌介绍了三个重要的数据结构:布隆过滤器(bloom filter),前缀树(prefix trie),环形缓冲(ring buffer)。
想当一个聪明程序员,这些结构你值得拥有!
【本文是51CTO专栏机构大数据文摘的原创译文,微信公众号“大数据文摘( id: BigDataDigest)”】