本文主要介绍,Python数据科学:正则化方法。正则化方法的出现,通过收缩方法(正则化方法)进行回归。
正则化方法主要包括岭回归与LASSO回归。
一、岭回归
岭回归通过人为加入的惩罚项(约束项),对回归系数进行估计,为有偏估计。
有偏估计,允许估计有不大的偏度,以换取估计的误差显著减小,并在其残差平方和为最小的原则下估计回归系数。
通常岭回归方程中的R²会稍低于线性回归分析,但回归系数的显著性往往明显高于普通线性回归。
这里不对相应的理论知识进行细说,说实话小F也是晕乎乎...
所以选择先调包,看看效果是啥样的。
使用机器学习框架scikit-learn进行岭回归参数的选择(正则化系数)。
数据是书中的数据,已上传网盘,公众号回复「正则化」,即可获取。
scikit-learn当中的模型不会默认对数据标准化,必须手动执行。
标准化后的数据可以消除量纲,让每个变量的系数在一定意义下进行直接比较。
- import numpy as np
- import pandas as pd
- import matplotlib.pyplot as plt
- from sklearn.linear_model import Ridge
- from sklearn.linear_model import RidgeCV
- from sklearn.preprocessing import StandardScaler
- # 消除pandas输出省略号情况及换行情况
- pd.set_option('display.max_columns', 500)
- pd.set_option('display.width', 1000)
- # 读取数据,skipinitialspace:忽略分隔符后的空白
- df = pd.read_csv('creditcard_exp.csv', skipinitialspace=True)
- # 获取信用卡有支出的行数据
- exp = df[df['avg_exp'].notnull()].copy().iloc[:, 2:].drop('age2', axis=1)
- # 获取信用卡无支出的行数据,NaN
- exp_new = df[df['avg_exp'].isnull()].copy().iloc[:, 2:].drop('age2', axis=1)
- # 选择4个连续变量,分别是年龄 收入 当地小区价格 当地人均收入
- continuous_xcols = ['Age', 'Income', 'dist_home_val', 'dist_avg_income']
- # 标准化
- scaler = StandardScaler()
- # 解释变量,二维数组
- X = scaler.fit_transform(exp[continuous_xcols])
- # 被解释变量,一维数组
- y = exp['avg_exp_ln']
- # 生成正则化系数
- alphas = np.logspace(-2, 3, 100, base=10)
- # 使用不同的正则化系数对模型进行交叉验证
- rcv = RidgeCV(alphas=alphas, store_cv_values=True)
- # 使用数据集训练(fit)
- rcv.fit(X, y)
- # 输出最优参数,正则化系数及相应模型R²
- print('The best alpha is {}'.format(rcv.alpha_))
- print('The r-square is {}'.format(rcv.score(X, y)))
- # 训练好后使用transform进行数据转换
- X_new = scaler.transform(exp_new[continuous_xcols])
- # 使用模型对数据做预测
- print(np.exp(rcv.predict(X_new)[:5]))
输出结果如下。
最优正则化系数为0.29,模型R²为0.475。
并使用最优正则化系数下的岭回归模型预测数据。
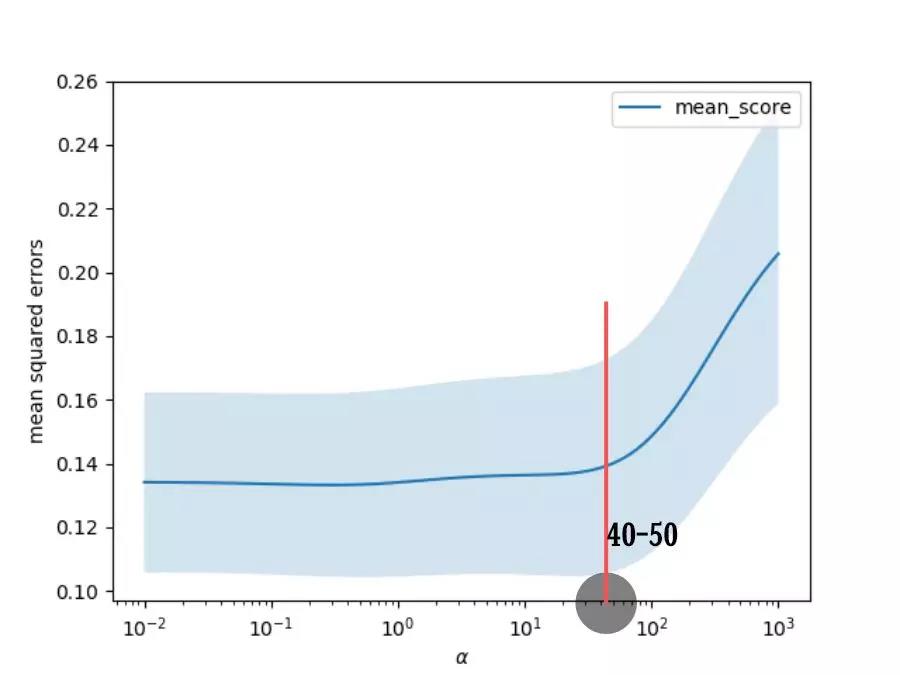
对不同正则化系数下模型的均方误差进行可视化。
- # 正则化系数搜索空间当中每轮交叉验证的结果,模型的均方误差
- cv_values = rcv.cv_values_
- n_fold, n_alphas = cv_values.shape
- # 模型均方误差上下波动值
- cv_mean = cv_values.mean(axis=0)
- cv_std = cv_values.std(axis=0)
- ub = cv_mean + cv_std / np.sqrt(n_fold)
- lb = cv_mean - cv_std / np.sqrt(n_fold)
- # 绘制折线图,x轴是指数型形式
- plt.semilogx(alphas, cv_mean, label='mean_score')
- # y1(lb)和y2(ub)之间进行填充
- plt.fill_between(alphas, lb, ub, alpha=0.2)
- plt.xlabel('$\\alpha$')
- plt.ylabel('mean squared errors')
- plt.legend(loc='best')
- plt.show()
输出结果如下。
发现正则化系数在40或50以下时,模型的均方误差相差不大。
当系数超过该阈值时,均方误差则快速上升。
所以正则化系数只要小于40或50,模型的拟合效果应该都不错。
- 正则化系数越小则模型拟合越好,但过拟合情况也越容易发生。
- 正则化系数越大,则越不容易过拟合,但模型的偏差越大。
RidgeCV通过交叉验证,可以快速返回“最优”的正则化系数。
当这只是基于数值计算的,可能最终结果并不符合业务逻辑。
比如本次模型的变量系数。
- # 输出模型的变量系数
- print(rcv.coef_)
- # 输出结果
- [ 0.03321449 -0.30956185 0.05551208 0.59067449]
发现收入的系数为负值,这肯定是不合理的。
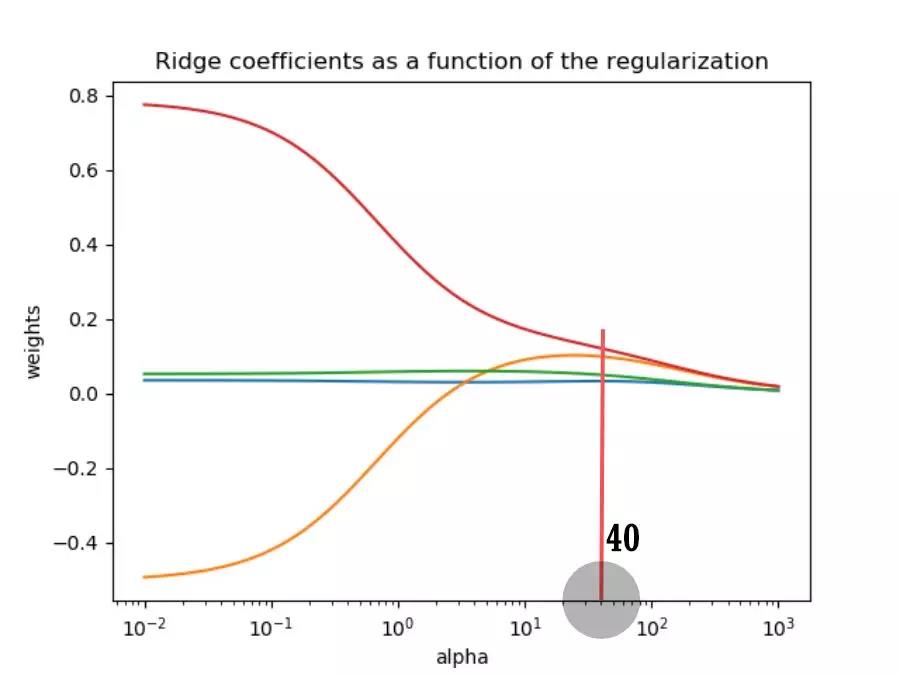
下面通过岭迹图进行进一步分析。
岭迹图是在不同正则化系数下变量系数的轨迹。
- ridge = Ridge()
- coefs = []
- # 不同正则化系数下的变量系数
- for alpha in alphas:
- ridge.set_params(alpha=alpha)
- ridge.fit(X, y)
- coefs.append(ridge.coef_)
- # 绘制变量系数随正则化系数变化的轨迹
- ax = plt.gca()
- ax.plot(alphas, coefs)
- ax.set_xscale('log')
- plt.xlabel('alpha')
- plt.ylabel('weights')
- plt.title('Ridge coefficients as a function of the regularization')
- plt.axis('tight')
- plt.show()
输出结果。
- ①有两个变量的系数在不同的正则化系数下都很接近于0,那么可以选择删除。
- ②正则化系数越大,对变量系数的惩罚越大,所有变量的系数都趋近于0。
- ③有一个变量的系数变化非常大(有正有负),说明该系数的方差大,存在共线性的情况。
综合模型均方误差和岭迹图的情况,选取正则化系数为40。
- 如果大于40,则模型均方误差增大,模型拟合效果变差。
- 如果小于40,则变量系数不稳定,共线性没有得到抑制。
那么就来看看,当正则化系数为40时,模型变量系数的情况。
- ridge.set_params(alpha=40)
- ridge.fit(X, y)
- # 输出变量系数
- print(ridge.coef_)
- # 输出模型R²
- print(ridge.score(X, y))
- # 预测数据
- print(np.exp(ridge.predict(X_new)[:5]))
- # 输出结果
- [0.03293109 0.09907747 0.04976305 0.12101456]
- 0.4255673043353688
- [934.79025945 727.11042209 703.88143602 759.04342764 709.54172995]
发现变量系数都为正值,符合业务直觉。
收入和当地人均收入这两个变量可以保留,另外两个删除。
二、LASSO回归
LASSO回归,在令回归系数的绝对值之和小于一个常数的约束条件下,使残差平方和最小化。
从而能够产生某些严格等于0的回归系数,得到解释力较强的模型。
相比岭回归,LASSO回归还可以进行变量筛选。
使用LassoCV交叉验证确定最优的正则化系数。
- # 生成正则化系数
- lasso_alphas = np.logspace(-3, 0, 100, base=10)
- # 使用不同的正则化系数对模型进行交叉验证
- lcv = LassoCV(alphas=lasso_alphas, cv=10)
- # 使用数据集训练(fit)
- lcv.fit(X, y)
- # 输出最优参数,正则化系数及相应模型R²
- print('The best alpha is {}'.format(lcv.alpha_))
- print('The r-square is {}'.format(lcv.score(X, y)))
- # 输出结果
- The best alpha is 0.04037017258596556
- The r-square is 0.4426451069862233
发现最优的正则化系数为0.04,模型R²为0.443。
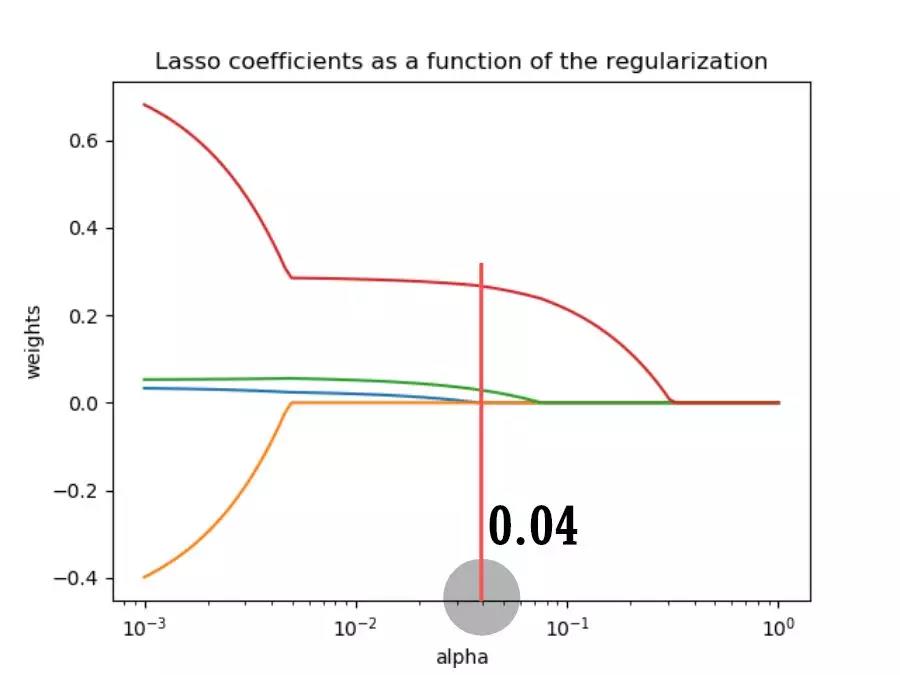
接下来获取不同正则化系数下的变量系数轨迹。
- lasso = Lasso()
- lasso_coefs = []
- # 不同正则化系数下的变量系数
- for alpha in lasso_alphas:
- lasso.set_params(alpha=alpha)
- lasso.fit(X, y)
- lasso_coefs.append(lasso.coef_)
- # 绘制变量系数随正则化系数变化的轨迹
- ax = plt.gca()
- ax.plot(lasso_alphas, lasso_coefs)
- ax.set_xscale('log')
- plt.xlabel('alpha')
- plt.ylabel('weights')
- plt.title('Lasso coefficients as a function of the regularization')
- plt.axis('tight')
- plt.show()
输出结果。
发现随着正则化系数的增大,所有变量的系数会在某一阈值突降为0。
其中缘由与LASSO回归方程有关,不细说。
输出LASSO回归的变量系数。
- print(lcv.coef_)
- # 输出结果
- [0. 0. 0.02789489 0.26549855]
发现前两个变量被筛选掉了,即年龄和收入。
为啥和岭回归的结果不一样呢???
三、总结
坑留的有点多,待小F慢慢填...