分离集合(disjoint set)是一种经典的数据结构,它有三类操作:
- Make-set(a):生成包含一个元素a的集合S;
- Union(X, Y):合并两个集合X和Y;
- Find-set(a):查找元素a所在集合S,即通过元素找集合句柄;
它非常适合用来解决集合合并与查找的问题,也常称为并查集。
一、并查集的链表实现
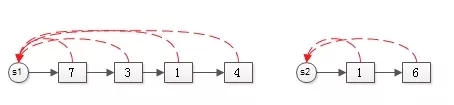
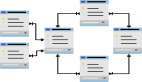
如上图,并查集可以用链表来实现。
(1) 链表实现的并查集,Find-set(a)的时间复杂度是多少?
集合里的每个元素,都指向“集合的句柄”,这样可以使得“查找元素a所在集合S”,即Find-set(a)操作在O(1)的时间内完成。
(2) 链表实现的并查集,Union(X, Y)的时间复杂度是多少?
假设有集合:
S1={7,3,1,4}
S2={1,6}
- 1.
- 2.
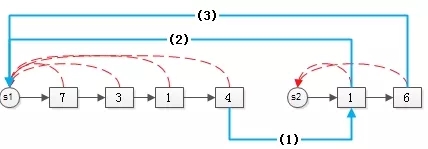
合并S1和S2两个集合,需要做两件事情:
- ***个集合的尾元素,链向第二个集合的头元素(蓝线1);
- 第二个集合的所有元素,指向***个集合的句柄(蓝线2,3);
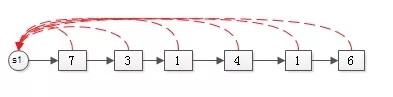
合并完的效果是:
变成了一个更大的集合S1。
集合合并时,将短的链表,往长的链表上接,这样变动的元素更少,这个优化叫做“加权合并”。
画外音:实现的过程中,集合句柄要存储元素个数,头元素,尾元素等属性,以方便上述操作进行。
假设每个集合的平均元素个数是n,Union(X, Y)操作的时间复杂度是O(n)。
(3) 能不能Find-set(a)与Union(X, Y)都在O(1)的时间内完成呢?
可以,这就引发了并查集的第二种实现方法。
二、并查集的有根树实现
(1) 什么是有根树,和普通的树有什么不同?
常用的set,就是用普通的二叉树实现的,其元素的数据结构是:
element{
int data;
element* left;
element* right;
}
- 1.
- 2.
- 3.
- 4.
- 5.
通过左指针与右指针,父亲节点指向儿子节点。
而有根树,其元素的数据结构是:
element{
int data;
element* parent;
}
- 1.
- 2.
- 3.
- 4.
通过儿子节点,指向父亲节点。
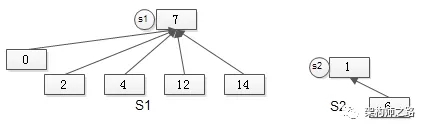
假设有集合:
S1={7,3,1,4}
S2={1,6}
- 1.
- 2.
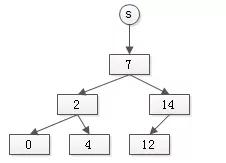
通过如果通过有根树表示,可能是这样的:
所有的元素,都通过parent指针指向集合句柄,所有元素的Find-set(a)的时间复杂度也是O(1)。
画外音:假设集合的***元素,代表集合句柄。
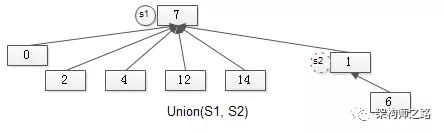
(2) 有根树实现的并查集,Union(X, Y)的过程如何?时间复杂度是多少?
通过有根树实现并查集,集合合并时,直接将一个集合句柄,指向另一个集合即可。
如上图所示,S2的句柄,指向S1的句柄,集合合并完成:S2消亡,S1变为了更大的集合。
容易知道,集合合并的时间复杂度为O(1)。
会发现,集合合并之后,有根树的高度变高了,与“加权合并”的优化思路类似,总是把节点数少的有根树,指向节点数多的有根树(更确切的说,是高度矮的树,指向高度高的树),这个优化叫做“按秩合并”。
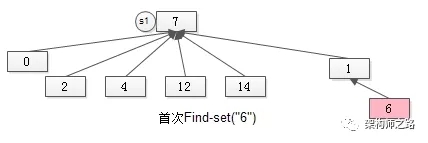
(3) 新的问题来了,集合合并之后,不是所有元素的Find-set(a)操作都是O(1)了,怎么办?
如图S1与S2合并后的新S1,***“通过元素6来找新S1的句柄”,不能在O(1)的时间内完成了,需要两次操作。
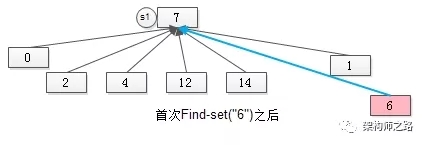
但为了让未来“通过元素6来找新S1的句柄”的操作能够在O(1)的时间内完成,在***进行Find-set(“6”)时,就要将元素6“寻根”路径上的所有元素,都指向集合句柄,如下图。
某个元素如果不直接指向集合句柄,***Find-set(a)操作的过程中,会将该路径上的所有元素都直接指向句柄,这个优化叫做“路径压缩”。
画外音:路径上的元素第二次执行Find-set(a)时,时间复杂度就是O(1)了。
实施“路径压缩”优化之后,Find-set的平均时间复杂度仍是O(1)。
结论
通过链表实现并查集:
- Find-set的时间复杂度,是O(1)常数时间
- Union的时间复杂度,是集合平均元素个数,即线性时间
画外音:别忘了“加权合并”优化。
通过有根树实现并查集:
- Union的时间复杂度,是O(1)常数时间
- Find-set的时间复杂度,通过“按秩合并”与“路径压缩”优化后,平均时间复杂度也是O(1)
使用并查集,非常适合解决“微信群覆盖”问题。
思路比结论重要,有收获就是好的。
【本文为51CTO专栏作者“58沈剑”原创稿件,转载请联系原作者】