直奔主题,世界上“最漂亮”的排序算法。
- void stooge_sort(int arr[], int i, int j){
- if (arr[i]>arr[j]) swap(arr[i], arr[j]);
- if (i+1>=j) return;
- int k=(j-i+1)/3;
- stooge_sort(arr, i, j-k);
- stooge_sort(arr, i+k, j);
- stooge_sort(arr, i, j-k);
- }
《算法导论》习题中的“完美排序”,由Howard、Fine等几个教授提出,之所以称为“完美排序”,是因为其代码实现,优雅、工整、漂亮。
代码不是很好理解,一步步讲解下思路。
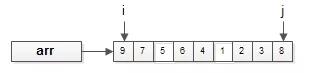
首先,排序传入的参数是待排序的数组arr[i, j];
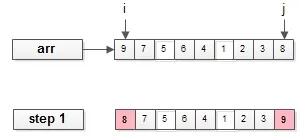
第一步:比较i与j位置的元素,根据排序规则决定是否进行置换。
画外音:本栗子,假设排序规则是从小到大。
置换完成后,判断排序是否结束,当i和j相邻时,排序结束。
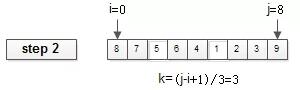
第二步:将arr[i, j]三等分;
画外音:总元素个数是j-i+1。
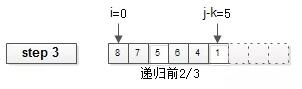
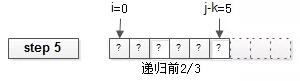
第三步:递归arr的前2/3半区。
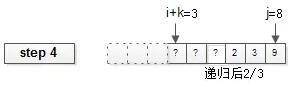
第四步:递归arr的后2/3半区。
第五步:递归arr的前2/3半区。
排序结束。
神奇不神奇!!!
再看一遍,印象深刻不?
- void stooge_sort(int arr[], int i, int j){
- if (arr[i]>arr[j]) swap(arr[i], arr[j]); // 比较
- if (i+1>=j) return; // 是否结束
- int k=(j-i+1)/3; // 三等分
- stooge_sort(arr, i, j-k); // 前2/3半区
- stooge_sort(arr, i+k, j); // 后2/3半区
- stooge_sort(arr, i, j-k); // 前2/3半区
- }
然并卵,除了代码好看,完美排序毛用没有,因为它是一个挺慢的算法。
由代码很容易看出来:
- 当只有1个元素时,完美排序的时间也是1;
- 当有n个元素时,完美排序由一个常数计算,加上三次递归,每次递归数据量为(2/3)*n;
即,其时间复杂度递归式为:
- T(1) = 1;
- T(n) = 3T(2/3n) + 1;
使用《搞定所有时间复杂度计算》中的递归式计算方法,最终得到,完美排序的时间复杂度是O(n^2.7),比O(n^2)的排序都要慢。
完美排序的排序证明,不在文章中展开。从代码直观能感受到,通过swap和三次递归,趋势上,小的元素会往前端走,大的元素会往后端走,直至完成排序。
画外音:快速排序的过程是partition+两次递归,也是小的元素往前端走,大的元素往后端走,直至完成排序。
希望这一分钟,大家有收获。
【本文为51CTO专栏作者“58沈剑”原创稿件,转载请联系原作者】