面试中,TopK,是问得比较多的几个问题之一,到底有几种方法,这些方案里蕴含的优化思路究竟是怎么样的,今天和大家聊一聊。
画外音:除非校招,我在面试过程中从不问TopK这个问题,默认大家都知道。
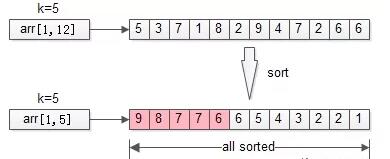
问题描述:从arr[1, n]这n个数中,找出***的k个数,这就是经典的TopK问题。
栗子:从arr[1, 12]={5,3,7,1,8,2,9,4,7,2,6,6} 这n=12个数中,找出***的k=5个。
一、排序
排序是最容易想到的方法,将n个数排序之后,取出***的k个,即为所得。
伪代码:
- sort(arr, 1, n);
- return arr[1, k];
时间复杂度:O(n*lg(n))
分析:明明只需要TopK,却将全局都排序了,这也是这个方法复杂度非常高的原因。那能不能不全局排序,而只局部排序呢?这就引出了第二个优化方法。
二、局部排序
不再全局排序,只对***的k个排序。
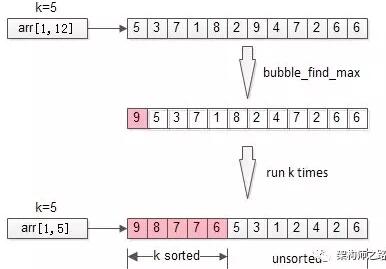
冒泡是一个很常见的排序方法,每冒一个泡,找出***值,冒k个泡,就得到TopK。
伪代码:
- for(i=1 to k){
- bubble_find_max(arr,i);
- }
- return arr[1, k];
时间复杂度:O(n*k)
分析:冒泡,将全局排序优化为了局部排序,非TopK的元素是不需要排序的,节省了计算资源。不少朋友会想到,需求是TopK,是不是这***的k个元素也不需要排序呢?这就引出了第三个优化方法。
三、堆
思路:只找到TopK,不排序TopK。
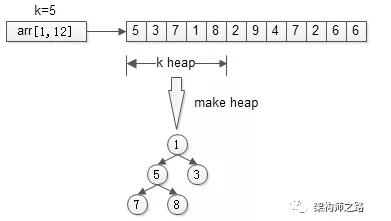
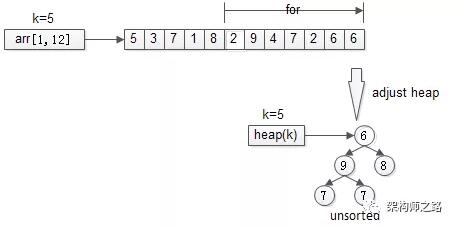
先用前k个元素生成一个小顶堆,这个小顶堆用于存储,当前***的k个元素。
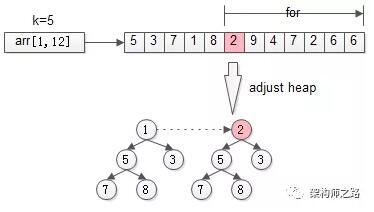
接着,从第k+1个元素开始扫描,和堆顶(堆中最小的元素)比较,如果被扫描的元素大于堆顶,则替换堆顶的元素,并调整堆,以保证堆内的k个元素,总是当前***的k个元素。
直到,扫描完所有n-k个元素,最终堆中的k个元素,就是猥琐求的TopK。
伪代码:
- heap[k] = make_heap(arr[1, k]);
- for(i=k+1 to n){
- adjust_heap(heep[k],arr[i]);
- }
- return heap[k];
时间复杂度:O(n*lg(k))
画外音:n个元素扫一遍,假设运气很差,每次都入堆调整,调整时间复杂度为堆的高度,即lg(k),故整体时间复杂度是n*lg(k)。
分析:堆,将冒泡的TopK排序优化为了TopK不排序,节省了计算资源。堆,是求TopK的经典算法,那还有没有更快的方案呢?
四、随机选择
随机选择算在是《算法导论》中一个经典的算法,其时间复杂度为O(n),是一个线性复杂度的方法。
这个方法并不是所有同学都知道,为了将算法讲透,先聊一些前序知识,一个所有程序员都应该烂熟于胸的经典算法:快速排序。
画外音:
- 如果有朋友说,“不知道快速排序,也不妨碍我写业务代码呀”…额...
- 除非校招,我在面试过程中从不问快速排序,默认所有工程师都知道;
其伪代码是:
- void quick_sort(int[]arr, int low, inthigh){
- if(low== high) return;
- int i = partition(arr, low, high);
- quick_sort(arr, low, i-1);
- quick_sort(arr, i+1, high);
- }
其核心算法思想是,分治法。
分治法(Divide&Conquer),把一个大的问题,转化为若干个子问题(Divide),每个子问题“都”解决,大的问题便随之解决(Conquer)。这里的关键词是“都”。从伪代码里可以看到,快速排序递归时,先通过partition把数组分隔为两个部分,两个部分“都”要再次递归。
分治法有一个特例,叫减治法。
减治法(Reduce&Conquer),把一个大的问题,转化为若干个子问题(Reduce),这些子问题中“只”解决一个,大的问题便随之解决(Conquer)。这里的关键词是“只”。
二分查找binary_search,BS,是一个典型的运用减治法思想的算法,其伪代码是:
- int BS(int[]arr, int low, inthigh, int target){
- if(low> high) return -1;
- mid= (low+high)/2;
- if(arr[mid]== target) return mid;
- if(arr[mid]> target)
- return BS(arr, low, mid-1, target);
- else
- return BS(arr, mid+1, high, target);
- }
从伪代码可以看到,二分查找,一个大的问题,可以用一个mid元素,分成左半区,右半区两个子问题。而左右两个子问题,只需要解决其中一个,递归一次,就能够解决二分查找全局的问题。
通过分治法与减治法的描述,可以发现,分治法的复杂度一般来说是大于减治法的:
- 快速排序:O(n*lg(n))
- 二分查找:O(lg(n))
话题收回来,快速排序的核心是:
- i = partition(arr, low, high);
1. 这个partition是干嘛的呢?
顾名思义,partition会把整体分为两个部分。
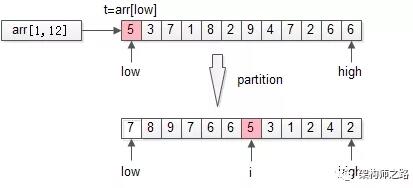
更具体的,会用数组arr中的一个元素(默认是***个元素t=arr[low])为划分依据,将数据arr[low, high]划分成左右两个子数组:
- 左半部分,都比t大
- 右半部分,都比t小
- 中间位置i是划分元素
以上述TopK的数组为例,先用***个元素t=arr[low]为划分依据,扫描一遍数组,把数组分成了两个半区:
- 左半区比t大
- 右半区比t小
- 中间是t
partition返回的是t最终的位置i。
很容易知道,partition的时间复杂度是O(n)。
画外音:把整个数组扫一遍,比t大的放左边,比t小的放右边,***t放在中间N[i]。
2. partition和TopK问题有什么关系呢?
TopK是希望求出arr[1,n]中***的k个数,那如果找到了第k大的数,做一次partition,不就一次性找到***的k个数了么?
画外音:即partition后左半区的k个数。
问题变成了arr[1, n]中找到第k大的数。
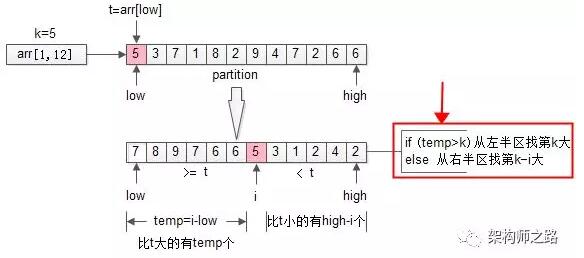
再回过头来看看***次partition,划分之后:
- i = partition(arr, 1, n);
- 如果i大于k,则说明arr[i]左边的元素都大于k,于是只递归arr[1, i-1]里第k大的元素即可;
- 如果i小于k,则说明说明第k大的元素在arr[i]的右边,于是只递归arr[i+1, n]里第k-i大的元素即可;
画外音:这一段非常重要,多读几遍。
这就是随机选择算法randomized_select,RS,其伪代码如下:
- int RS(arr, low, high, k){
- if(low== high) return arr[low];
- i= partition(arr, low, high);
- temp= i-low; //数组前半部分元素个数
- if(temp>=k)
- return RS(arr, low, i-1, k); //求前半部分第k大
- else
- return RS(arr, i+1, high, k-i); //求后半部分第k-i大
- }
这是一个典型的减治算法,递归内的两个分支,最终只会执行一个,它的时间复杂度是O(n)。
再次强调一下:
- 分治法,大问题分解为小问题,小问题都要递归各个分支,例如:快速排序
- 减治法,大问题分解为小问题,小问题只要递归一个分支,例如:二分查找,随机选择
通过随机选择(randomized_select),找到arr[1, n]中第k大的数,再进行一次partition,就能得到TopK的结果。
五、总结
TopK,不难;其思路优化过程,不简单:
- 全局排序,O(n*lg(n))
- 局部排序,只排序TopK个数,O(n*k)
- 堆,TopK个数也不排序了,O(n*lg(k))
- 分治法,每个分支“都要”递归,例如:快速排序,O(n*lg(n))
- 减治法,“只要”递归一个分支,例如:二分查找O(lg(n)),随机选择O(n)
- TopK的另一个解法:随机选择+partition
【本文为51CTO专栏作者“58沈剑”原创稿件,转载请联系原作者】