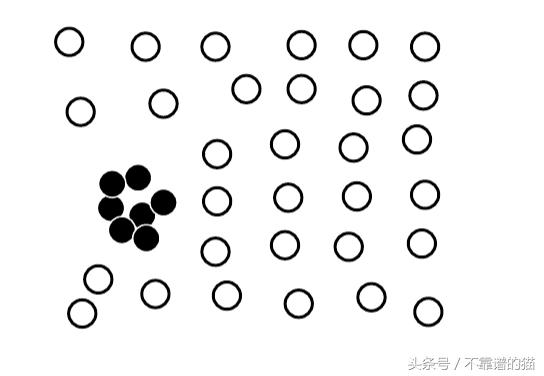
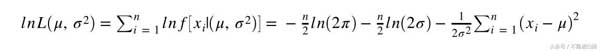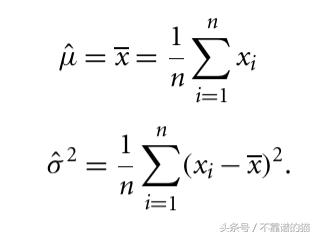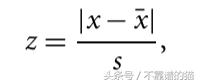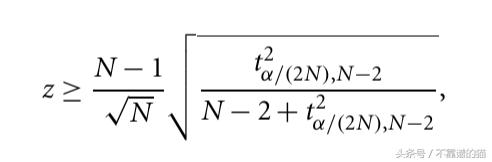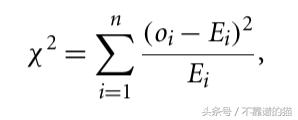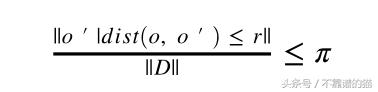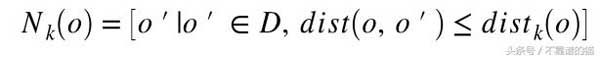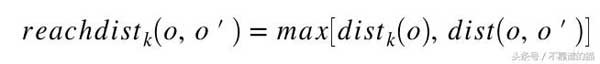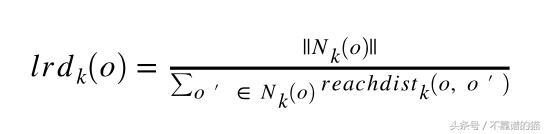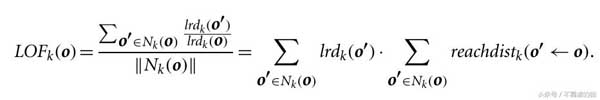异常值检测(也称为异常检测)是机器学习中查找具有与期望非常不同的行为的数据对象的过程。这些对象称为离群值或异常。
最有趣的对象是那些与普通对象明显不同的对象。离群值不是由与其他数据相同的机制生成的。
异常检测在许多应用中很重要,例如:
- 财务数据欺诈
- 通信网络中的入侵
- 假新闻和错误信息
- 医疗分析
- 行业损坏检测
- 安全和监视
- 等等
离群值检测和聚类分析是两个高度相关的任务。聚类在机器学习数据集中查找多数模式并相应地组织数据,而离群值检测尝试捕获那些与多数模式大不相同的异常情况。
在本文中,我将介绍异常值检测的基本方法,并重点介绍一类Proximity-based算法方法。我还将提供LOF算法的代码实现。
异常值和噪声数据
首先在机器学习中,您需要将离群值与噪声数据区分开来。
应用离群检测时应去除噪音。它可能会扭曲正常对象并模糊正常对象和离群值之间的区别。它可能有助于隐藏离群值并降低离群值检测的有效性。例如,如果用户考虑购买他过去经常购买的更昂贵的午餐,则应将此行为视为“噪音交易”,如“random errors”或“variance”。
异常值的类型
通常,异常值可以分为三类,即全局异常值,上下文(或条件)异常值和集体异常值。
- 全局异常值 - 对象显着偏离数机器学习据集的其余部分
- 上下文异常值 - 对象根据选定的上下文显着偏离。例如,28⁰C是莫斯科冬季的异常值,但在另一个背景下不是异常值,28⁰C不是莫斯科夏季的异常值。
- 集合异常值 - 即使单个数据对象可能不是异常值,数据对象的子集也会显着偏离整个机器学习数据集。例如,短期内小方的同一股票的大量交易可以被视为市场操纵的证据。
集合异常值
通常,数据集可以包含不同类型的异常值,并且同时可以属于不止一种类型的异常值。
异常值检测方法
文献中涵盖了许多异常值检测方法,并在实践中使用。首先,异常值检测方法根据用于分析的数据样本是否与领域专家提供的标签一起给出,该标签可用于构建异常值检测模型。其次,可以根据关于正常对象与异常值的假设将方法分成组。
如果可以获得正常和/或异常对象的专家标记示例,则可以使用它们来构建异常值检测模型。使用的方法可以分为监督方法,半监督方法和无监督方法。
监督方法
我们将离群值检测建模为分类问题。由领域专家检查的样本用于训练和测试。
挑战:
- 类不平衡。也就是说,异常值的数量通常远小于普通对象的数量。可以使用处理不平衡类的方法,例如过采样。
- 捕获尽可能多的异常值,即,召回比准确性更重要(即,不将正常对象误标记为异常值)
无监督的方法
在某些应用程序方案中,标记为“正常”或“异常”的对象不可用。因此,必须使用无监督学习方法。无监督异常值检测方法做出了一个隐含的假设:正常对象在某种程度上是“聚类的”。换句话说,无监督异常值检测方法期望正常对象比异常值更频繁地遵循模式。
挑战:
- 普通对象可能不共享任何强模式,但是集合异常值可能在小区域中具有高相似性
- 如果正常活动是多样的并且不属于高质量聚类,则无监督方法可能具有高误报率并且可能使许多实际异常值不受影响。
最新的无监督方法开发了智能想法,直接解决异常值而无需明确检测聚类。
半监督方法
在许多应用中,虽然获得一些标记的示例是可行的,但是这种标记的示例的数量通常很小。如果有一些标记的普通对象可用:
- 使用带标签的示例和邻近的未标记对象来训练普通对象的模型
- 那些不适合普通对象模型的对象被检测为异常值
- 如果只有一些标记的异常值可用,则少量标记的异常值可能无法很好地覆盖可能的异常值。
统计方法
统计方法(也称为基于模型的方法)假设正常数据遵循一些统计模型(随机模型)。我们的想法是学习适合给定数据集的生成模型,然后将模型的低概率区域中的对象识别为异常值。
参数方法
参数方法假设通过参数θ的参数分布生成正常数据对象。参数分布f(x, θ )的概率密度函数给出了通过分布生成对象x的概率。该值越小,x越可能是异常值。
正常对象出现在随机模型的高概率区域中,而低概率区域中的对象是异常值。
统计方法的有效性在很大程度上取决于分配的假设。
例如,考虑具有正态分布的单变量数据。我们将使用最大似然法检测异常值。
估计参数μ和σ的最大似然法
取μ和σ²的导数并求解所得的一阶条件系统导致以下最大似然估计
μ和σ²的最大似然估计
看下Python示例:
- import numpy as np
- avg_temp = np.array([24.0, 28.9, 28.9, 29.0, 29.1, 29.1, 29.2, 29.2, 29.3, 29.4]) mean = avg_temp.mean()
- std = avg_temp.std()
- sigma = std^2
- print (mean, std, sigma) //28.61 1.54431214461 2.3849
最偏离的值是24⁰,远离平均值4.61。我们知道μ+/-3σ区域在正态分布假设下包含97%的数据。因为4.61 / 1.54> 3我们认为24⁰是异常值。
我们还可以使用另一种统计方法,称为Gribbs测试并计算z得分。
s - 标准偏差
但是我们很少使用只有一个属性的数据。涉及两个或多个属性的数据称为多变量。这些方法的核心思想是将多变量数据转换为单变量异常值检测问题。
流行的方法之一是 ² -statistics。
Oi - 第i维度中O的值。Ei - 所有对象中第i维的平均值,n维度。
如果χ²-大,则对象是异常值。
参数模型的主要缺点是在许多情况下,数据分布可能是未知的。
例如,如果我们有两个大的集合,那么关于正态分布的假设就不会很好。
相反,我们假设正常数据对象由多个正态分布Θ(μ1,σ1)和Θ(μ2,σ2)生成,并且对于数据集中的每个对象o,我们计算由分布的混合生成的概率。
Pr(o |Θ1,Θ2)=fΘ1(o)+fΘ2(o)
其中fΘ1(o) - Θ1和Θ2的概率密度函数。要学习参数μ和σ,我们可以使用EM算法。
非参数方法
在用于离群值检测的非参数方法中,从输入数据中学习“正常数据”模型,而不是先验地假设。非参数方法通常对数据做出较少的假设,因此可适用于更多场景。作为一个例子,我们可以使用直方图。
在最简单的方法中,如果对象在一个直方图箱中失败,则认为是正常的。缺点 - 很难选择垃圾箱尺寸。
Proximity-based算法
给定特征空间中的一组对象,可以使用距离度量来量化对象之间的相似性。直觉上,远离其他对象的对象可被视为异常值。Proximity-based方法假设异常值对象与其最近邻居的接近度明显偏离对象与数据集中的大多数其他对象的接近度。
Proximity-based算法可以分为基于距离(如果对象是没有足够的点,则对象是异常值)和基于密度的方法(如果对象的密度相对远低于其邻居,则对象是异常值)
基于密度
基于距离的离群值检测方法参考对象的邻域,该对象由给定半径定义。如果对象的邻域没有足够的其他点,则该对象被视为异常值。
阈值的距离,可以定义为对象的合理邻域。对于每个对象,我们可以找到对象的合理neighbours数量。
令r(r> 0)为距离阈值,π (0 <π<1)为分数阈值。对象o是DB(r, π )
DIST -距离测量
需要O(n²)时间。
挖掘基于距离的异常值的算法:
- 基于索引的算法
- 嵌套循环算法
- 基于单元的算法
基于密度的方法
基于密度的离群点检测方法研究对象的密度及其相邻对象的密度。在这里,如果一个对象的密度相对于其相邻对象的密度要低得多,那么这个对象就是一个离群值。
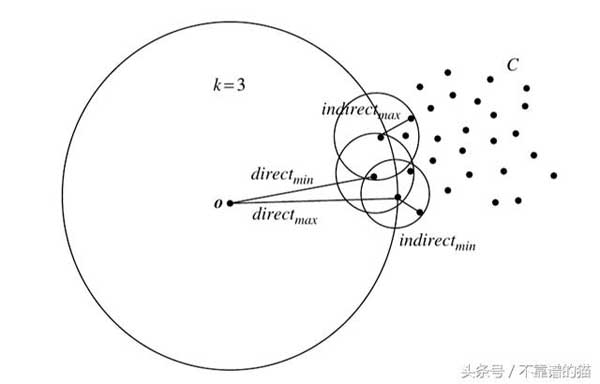
许多真实世界的数据集展示了一个更复杂的结构,其中对象可能被视为与其局部neighbours相关的离群值,而不是与全局数据分布相关的离群值。
考虑上面的例子,基于距离的方法能够检测到o3,但是对于o1和o2,它并不那么明显。
基于密度的想法是我们需要将对象周围的密度与其局部neighbours周围的密度进行比较。基于密度的离群值检测方法的基本假设是,非离群对象周围的密度类似于其neighbours周围的密度,而离群对象周围的密度与其邻近对象周围的密度明显不同。
dist_k(o)——对象o与k近邻之间的距离。o的k-distance邻域包含所有到o的距离不大于o的k-th距离dist_k(o)
我们可以用Nk(o)到o的平均距离作为o的局部密度的度量,如果o有非常接近的邻域o',使得dist(o,o')非常小,那么距离度量的统计波动可能会非常高。为了克服这个问题,我们可以通过添加平滑效果切换到以下可达距离测量。
k是用户指定的参数,用于控制平滑效果。基本上,k指定要检查的最小邻域以确定对象的局部密度。可达距离是不对称的。
对象o的局部可达性密度是
我们计算对象的局部可达性密度,并将其与其相邻的可比性密度进行比较,以量化对象被视为异常值的程度。
局部异常因子是o的局部可达性密度与o的 k近邻的比率的平均值。o的局部可达性密度越低,k的最近邻点的局部可达性密度越高,LOF值越高。这恰好捕获了局部密度相对较低的局部密度相对较低的局部异常值。它的k近邻。
LOF算法
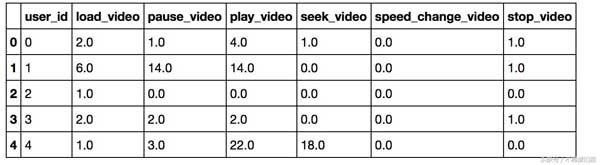
基于data.csv中的点击流事件频率模式,我们将应用LOF算法来计算每个点的LOF,并具有以下初始设置:
- k = 2并使用曼哈顿距离。
- k = 3并使用欧几里德距离。
结果,我们将找到5个异常值及其LOF_k(o)
可以从github 存储库下载数据(https://github.com/zkid18/Machine-Learning-Algorithms)
Python实现如下:
- import pandas as pd
- import seaborn as sns
- from scipy.spatial.distance import pdist, squareform
- data_input = pd.read_csv('../../data/clikstream_data.csv')
- #Reachdist function
- def reachdist(distance_df, observation, index):
- return distance_df[observation][index]
- #LOF algorithm implementation from scratch
- def LOF_algorithm(data_input, distance_metric = "cityblock", p = 5):
- distances = pdist(data_input.values, metric=distance_metric)
- dist_matrix = squareform(distances)
- distance_df = pd.DataFrame(dist_matrix)
- k = 2 if distance_metric == "cityblock" else 3
- observations = distance_df.columns
- lrd_dict = {}
- n_dist_index = {}
- reach_array_dict = {}
- for observation in observations:
- dist = distance_df[observation].nsmallest(k+1).iloc[k]
- indexes = distance_df[distance_df[observation] <= dist].drop(observation).index
- n_dist_index[observation] = indexes
- reach_dist_array = []
- for index in indexes:
- #make a function reachdist(observation, index)
- dist_between_observation_and_index = reachdist(distance_df, observation, index)
- dist_index = distance_df[index].nsmallest(k+1).iloc[k]
- reach_dist = max(dist_index, dist_between_observation_and_index)
- reach_dist_array.append(reach_dist)
- lrd_observation = len(indexes)/sum(reach_dist_array)
- reach_array_dict[observation] = reach_dist_array
- lrd_dict[observation] = lrd_observation
- #Calculate LOF
- LOF_dict = {}
- for observation in observations:
- lrd_array = []
- for index in n_dist_index[observation]:
- lrd_array.append(lrd_dict[index])
- LOF = sum(lrd_array)*sum(reach_array_dict[observation])/np.square(len(n_dist_index[observation]))
- LOF_dict[observation] = LOF
- return sorted(LOF_dict.items(), key=lambda x: x[1], reverse=True)[:p]
- LOF_algorithm(data_input, p = 5)
- # [(19, 11.07),
- # (525, 8.8672286617492091),
- # (66, 5.0267857142857144),
- # (638, 4.3347272196829723),
- # (177, 3.6292633292633294)]
- LOF_algorithm(data_input, p = 5, distance_metric = 'euclidean')
- # [(638, 3.0800716645705695),
- # (525, 3.0103162562616288),
- # (19, 2.8402916620868903),
- # (66, 2.8014102661691211),
- # (65, 2.6456528412196416)]