1.字母转换问题
题目要求:
你得到一个可能混合大小写字母的字符串,你的任务是把该字符串转为仅使用小写字母或者大写字母,为了尽可能少的改变:
如果字符串包含的大字母数小于等于小写字母数,则把字符串转为小写。
如果大写的数目大于小写字母数,则把字符串转为全大写。
比如:
- solve('coDe')=="code"
- solve("CODe")=="CODE"
这道题稍微简单一点,怎么解呢:
1).屌丝解法:
对字符串中的每个字符进行判断大写还是小写
大写则计数+1,小写也+1
比较两种计数的大小,然后对字符串进行大小写反转
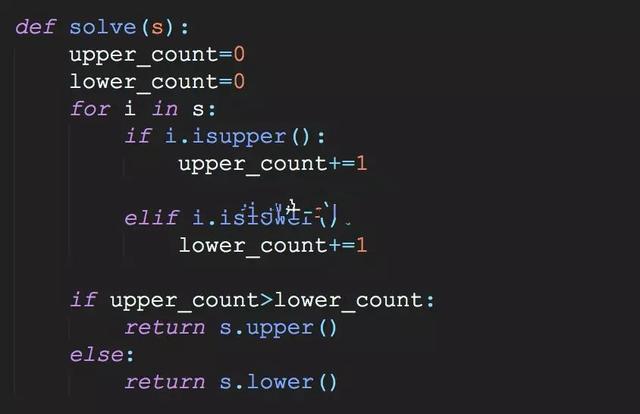
2).进阶解法
稍微把算法优化一下,我们对小写的取-1,大写的取1,然后计算和。
大于0则全部大写,否则则全部小写

3).高手解法
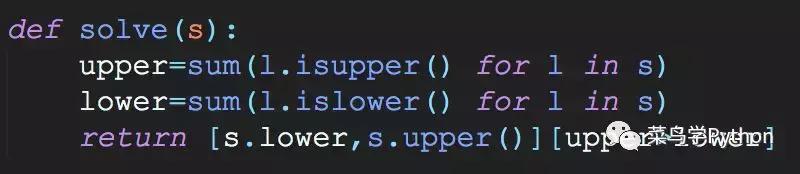
这种解法绝对让人拍案叫绝,值得思考。
2.数独问题
题目要求:
写一个函数检验数独是否完成:
- 如果完成,返回 “Finished!”
- 如果未完成,返回 “Try again!”
数独规则
- 数独为9行9列。
- 每一行和每一列均由 [1-9] 9个不重复数字组成。
- 将 9行x9列 的数独分割为9个小区域,每个区域3行3列,且保证每个小区域数字也是从[1-9] 9 个不重复数组成。
屌丝解题思路:
- board = [
- [1, 3, 2, 5, 7, 9, 4, 6, 8],
- [4, 9, 8, 2, 6, 1, 3, 7, 5],
- [7, 5, 6, 3, 8, 4, 2, 1, 9],
- [6, 4, 3, 1, 5, 8, 7, 9, 2],
- [5, 2, 1, 7, 9, 3, 8, 4, 6],
- [9, 8, 7, 4, 2, 6, 5, 3, 1],
- [2, 1, 4, 9, 3, 5, 6, 8, 7],
- [3, 6, 5, 8, 1, 7, 9, 2, 4],
- [8, 7, 9, 6, 4, 2, 1, 3, 5]
- ]
1).可以将上边列表看成一个矩阵图形
首先要满足的条件是行和列都必须由[1-9] 9个不重复的数组成。判断行是否满足条件:遍历列表 board,然后对每个元素(行)进行去重然后计算长度,生成一个新列表
- row_len=[len(set(row)) for row in board]
- # 结果为:
- [9, 9, 9, 9, 9, 9, 9, 9, 9]
- # 说明每一行去重后仍有9个元素,说明没有重复元素
- # ***只需要判断新生成的列表row_len 元素之和是否等于 81,就可以知道每一行是否有重复数字。
2).判断列是否满足条件
将 board 行列转换,然后像判断行一样进行判断
- board2 = map(list,zip(*board))
- # 结果:
- [[1, 4, 7, 6, 5, 9, 2, 3, 8],
- [3, 9, 5, 4, 2, 8, 1, 6, 7],
- [2, 8, 6, 3, 1, 7, 4, 5, 9],
- [5, 2, 3, 1, 7, 4, 9, 8, 6],
- [7, 6, 8, 5, 9, 2, 3, 1, 4],
- [9, 1, 4, 8, 3, 6, 5, 7, 2],
- [4, 3, 2, 7, 8, 5, 6, 9, 1],
- [6, 7, 1, 9, 4, 3, 8, 2, 3],
- [8, 5, 9, 2, 6, 1, 7, 4, 5]]
3).***判断行和列是否都满足条件
- def done_or_not(board):
- if sum([len(set(col)) for col in board2]) == 81 and sum([len(set(row)) for row in board]) ==81 :
- pass
- else:
- return 'Try again!'
4).怎么分成9个小块呢
使用numpy 将列表转换为 array ,然后使用切片很方便的得到小区域,例如:
import numpy as np
board_array = np.array(board)
board_array[0:3,0:3] #取***行到第三行,第1列到第3列的,3x3小区块
#结果:
- import numpy as np
- board_array = np.array(board)
- board_array[0:3,0:3] #取***行到第三行,第1列到第3列的,3x3小区块
- #结果:
- array([[1, 3, 2],
- [4, 9, 8],
- [7, 5, 6]])
- 那分成9个小区块就是:
- board_array[0:3,0:3]
- board_array[0:3,3:6]
- board_array[0:3,6:9]
- board_array[3:6,0:3]
- board_array[3:6,3:6]
- board_array[3:6,6:9]
- board_array[6:9,0:3]
- board_array[6:9,3:6]
- board_array[6:9,6:9]
可以看到每个小区块也是一个二维列表,将二维列表转成一维列表后进行去重就可以知道这个小区块有没有重复出现的数字,进而可以判断是否符合数独条件。
- import numpy as np
- def done_or_not(board):
- board2 = map(list,zip(*board))
- if sum([len(set(row)) for row in board2]) == 81 and sum([len(set(row)) for row in board]) ==81 :
- board_array = np.array(board)
- x = [0,3,6,9]
- for y in range(0,len(x)-1):
- for j in range(0,len(x)-1):
- z = board_array[x[y]:x[y+1],x[j]:x[j+1]]
- if len(set([num for row in z for num in row ])) != 9:
- return 'Try again!'
- return 'Finished!'
- else:
- return 'Try again!'
2.看高手的解法
涉及到多维数组的处理,可以直接用numpy里面的vstack来处理,会简洁和方便
- import numpy as np
- def done_or_not(aboard): #board[i][j]
- board = np.array(aboard)
- rows = [board[i,:] for i in range(9)] # 取行
- cols = [board[:,j] for j in range(9)] #取列
- sqrs = [board[i:i+3,j:j+3].flatten() for i in [0,3,6] for j in [0,3,6]] # 分区
- for view in np.vstack((rows,cols,sqrs)):
- if len(np.unique(view)) != 9:
- return 'Try again!'
- return 'Finished!'
3.神一样的解法
在上面用numpy的基础上,进一步巧妙的利用not all的用法
- import numpy as np
- def done_or_not(board):
- rows = np.array(board)
- cols = np.transpose(rows)
- subs = [np.ndarray.flatten(rows[x:x+3, y:y+3]) for x in range(0,9,3) for y in range(0,9,3)]
- for test in [rows, cols, subs]:
- if not all(sorted(group) == range(1,10) for group in test):
- return 'Try again!'
- return 'Finished!'
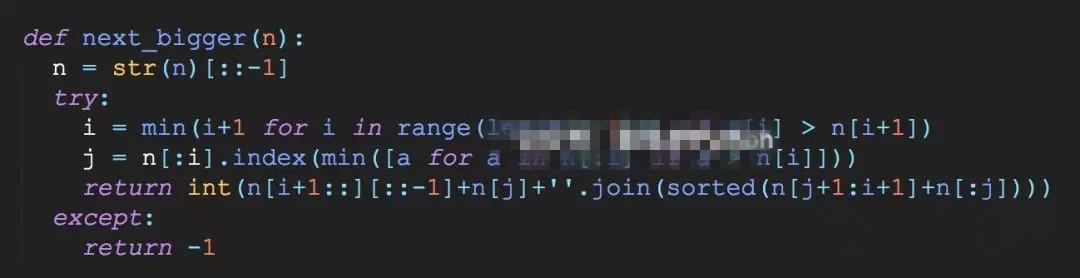
3.找出下一个大的数字
题目:
给定一个数字比如138,找出这个数字组合后下一个大的数字,比如138,183,318,813,831,很显然下一个大一点的数字是183。
这道题怎么解呢:
1).屌丝解法:
我们用最简单的暴力破解,先把数字转为字符列表,然后排列组合所有的情况,再把字符转给数字,然后排序,取比原来数字大的那一个就行了。
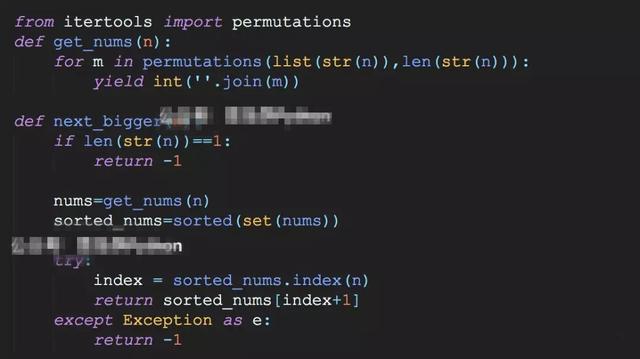
- 首先我们利用itertool库里面的牛逼闪闪的permutations,可以对一个列表进行全排序
- 接着我们把排序好的字符里面,用迭代器合成为一个一个数字
- 把数字列表进行从大到小的排序,找出比当前数字大的数字,即index+1
- 如果没有报错,则返回为-1
我们用assert测一下看看:
- assert next_bigger(50)==-1
- assert next_bigger(13)==31
- assert next_bigger(217)==271
- assert next_bigger(16318)==16381
完全正确,那么上面的解法有什么缺点吗,确实就是耗时,比如我们现在一个15位的数字需要查询,全排序显然不是上策!我们接着看第二种:
2).优化算法,进阶解法
既然全排序不行,那就要想一个算法来解决这个问题,比如16318,显然16381是比它大的,因为我是倒着来的,个位数比十位数大,那么取反之后就可以得到一个比原来大的数字。所以我们的思路:
- 我们是反向操作:从n个位开始依次和n+1(十位),n+2(百位),n+3(千位),n+4(万位)...进行比较
- 如果发现有大的数字,把n插入到n+1那里,同时把原来的n挪走,得到一个新的数字,放入我们的新列表
- 个位循环完毕,循环十位,依次重复上面的算法
- ***在新的列表中找出最小的那个数字就行了!
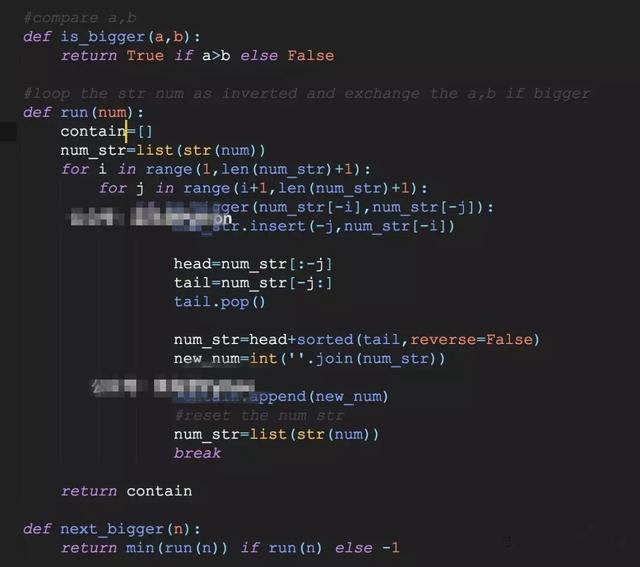
3).神一样的解法