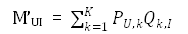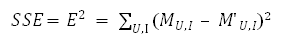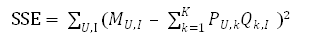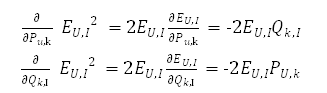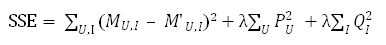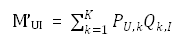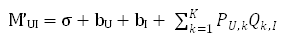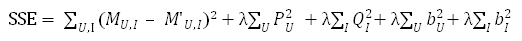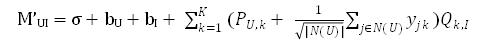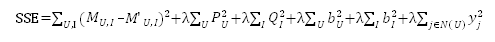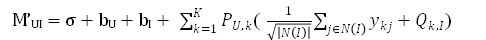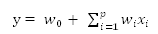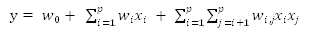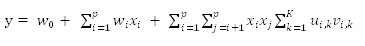随着大数据时代的来临，网络中的信息量呈现指数式增长，随之带来了信息过载问题。推荐系统是大数据时代下应运而生的产物，目前已广泛应用于电商、社交、短视频等领域。本文将针对推荐系统中基于隐语义模型的矩阵分解技术来进行讨论。
1、评分矩阵、奇异值分解与FunkSVD
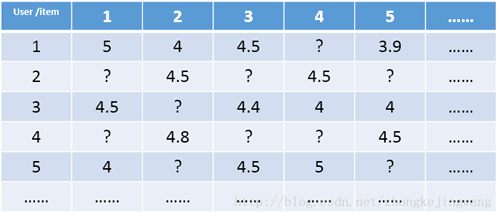
对于一个推荐系统，其用户数据可以整理成一个user-item矩阵。矩阵中每一行代表一个用户，而每一列则代表一个物品。若用户对物品有过评分，则矩阵中处在用户对应的行与物品对应的列交叉的位置表示用户对物品的评分值。这个user-item矩阵被称为评分矩阵。
上图即为评分矩阵的一个例子。其中的？表示用户还没有对物品做出评价，而推荐系统最终的目标就是对于任意一个用户，预测出所有未评分物品的分值，并按分值从高到低的顺序将对应的物品推荐给用户。
说到矩阵分解技术，首先想到的往往是特征值分解（eigendecomposition）与奇异值分解（Singular value decomposition，SVD）。
对于特征值分解，由于其只能作用于方阵，因此并不适合分解评分矩阵这个场景。
而对于奇异值分解，其具体描述为假设矩阵M是一个m*n的矩阵，则一定存在一个分解M=UΣVT，其中U是m*m的正交矩阵，V是n*n的正交矩阵，Σ是m*n的对角阵，可以说是完美契合分解评分矩阵这个需求了。其中，对角阵Σ还有一个特殊的性质，它的所有元素都非负，且依次减小。这个减小也特别快，在很多情况下，前10%的和就占了全部元素之和的99%以上，这就是说我们可以使用最大的k个值和对应大小的U、V矩阵来近似描述原始的评分矩阵。
于是我们马上能得到一个解决方案：对原始评分矩阵M做奇异值分解，得到U、V及Σ，取Σ中较大的k类作为隐含特征，则此时M(m*n)被分解成U(m*k) Σ(k*k)V(k*n)，接下来就可以直接使用矩阵乘法来完成对原始评分矩阵的填充。但是实际上，这种方法存在一个致命的缺陷——奇异值分解要求矩阵是稠密的。也就是说SVD不允许待分解矩阵中存在空白的部分，这一开始就与我们的问题所冲突了。当然，也可以想办法对缺失值先进行简单的填充，例如使用全局平均值。然而，即使有了补全策略，在实际应用场景下，user和item的数目往往是成千上万的，面对这样的规模传统SVD算法O(n^3)的时间复杂度显然是吃不消的。因此，直接使用传统SVD算法并不是一个好的选择。
既然传统SVD在实际应用场景中面临着稀疏性问题和效率问题，那么有没有办法避开稀疏问题，同时提高运算效率呢？
实际上早在2006年，Simon Funk就提出了FunkSVD算法，其主要思路是将原始评分矩阵M（m*n）分解成两个矩阵P（m*k）和Q（k*n），同时仅考察原始评分矩阵中有评分的项分解结果是否准确，而判别标准则是均方差。
即对于矩阵M(m*n)，我们想办法将其分解为P(m*k)、Q(k*n)，此时对于原始矩阵中有评分的位置MUI来说，其在分解后矩阵中对应的值就是：
那么对于整个评分矩阵而言，总的损失就是：
只要我们能想办法最小化上面的损失SSE，就能以最小的扰动完成对原始评分矩阵的分解，在这之后只需要用计算M’ 的方式来完成对原始评分矩阵的填充即可。
这种方法被称之为隐语义模型（Latent factor model，LFM），其算法意义层面的解释为通过隐含特征（latent factor）将user兴趣与item特征联系起来。
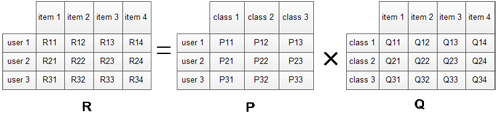
对于原始评分矩阵R，我们假定一共有三类隐含特征，于是将矩阵R（3*4）分解成用户特征矩阵P（3*3）与物品特征矩阵Q（3*4）。考察user1对item1的评分，可以认为user1对三类隐含特征class1、class2、class3的感兴趣程度分别为P11、P12、P13，而这三类隐含特征与item1相关程度则分别为Q11、Q21、Q31。
回到上面的式子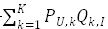
，可以发现用户U对物品I最终的评分就是由各个隐含特征维度下U对I感兴趣程度的和，这里U对I的感兴趣程度则是由U对当前隐含特征的感兴趣程度乘上I与当前隐含特征相关程度来表示的。
于是，现在的问题就变成了如何求出使得SSE最小的矩阵P和Q。
2、随机梯度下降法
在求解上文中提到的这类无约束最优化问题时，梯度下降法（Gradient Descent）是最常采用的方法之一，其核心思想非常简单，沿梯度下降的方向逐步迭代。梯度是一个向量，表示的是一个函数在该点处沿梯度的方向变化最快，变化率最大，而梯度下降的方向就是指的负梯度方向。
根据梯度下降法的定义，其迭代最终必然会终止于一阶导数（对于多元函数来说则是一阶偏导数）为零的点，即驻点。对于可导函数来说，其极值点一定是驻点，而驻点并不一定是极值点，还可能是鞍点。另一方面，极值点也不一定是最值点。下面举几个简单的例子。
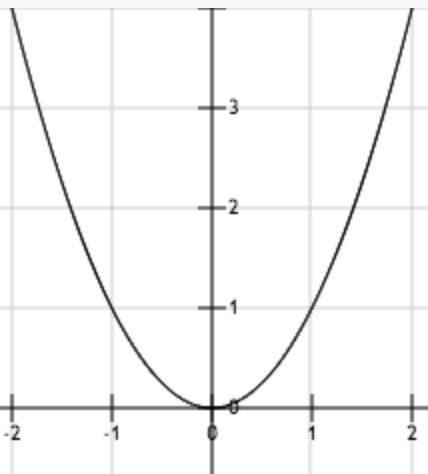
上图为函数y = x2。从图中可以看出，函数唯一的驻点 （0，0）为其最小值点。
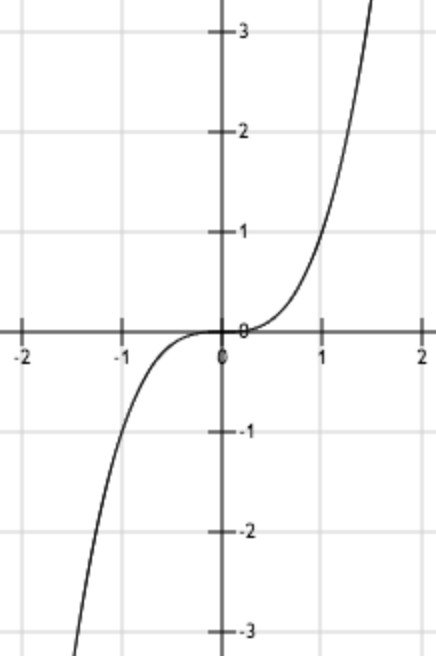
上图为函数y = x3。其一阶导数为3x2，从而可知其同样有唯一驻点 （0，0）。从图中可以看出，函数并没有极值点。
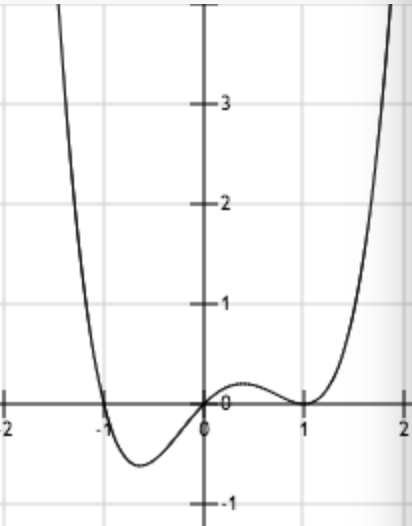
上图为函数y = x4 - x3 – x2 + x。从图像中可以看出，函数一共有三个驻点，包括两个极小值点和一个极大值点，其中位于最左边的极小值点是函数的最小值点。
上图为函数z = x2 - y2。其中点 （0，0，0）为其若干个鞍点中的一个。
从上面几幅函数图像中可以看出梯度下降法在求解最小值时具有一定的局限性，用一句话概括就是，目标函数必须是凸函数。关于凸函数的判定，对于一元函数来说，一般是求二阶导数，若其二阶导数非负，就称之为凸函数。对于多元函数来说判定方法类似，只是从判断一元函数的单个二阶导数是否非负，变成了判断所有变量的二阶偏导数构成的黑塞矩阵（Hessian Matrix）是否为半正定矩阵。判断一个矩阵是否半正定可以判断所有特征值是否非负，或者判断所有主子式是否非负。
回到上面funk svd的最优化问题上来。经过一番紧张刺激的计算之后，可以很遗憾地发现，我们最终的目标函数是非凸的。这就意味着单纯使用梯度下降法可能会找到极大值、极小值或者鞍点。这三类点的稳定性按从小到大排列依次是极大值、鞍点、极小值，考虑实际运算中，浮点数运算都会有一定的误差，因此最终结果很大几率会落入极小值点，同时也有落入鞍点的概率，而对于极大值点，除非初始值就是极大值，否则几乎不可能到达极大值点。
为了从鞍点和极小值点中脱出，在梯度下降法的基础上衍生出了各式各样的改进算法，例如动态调整步长（即学习率），利用上一次结果的动量法，以及随机梯度下降法 （Stochastic Gradient Descent， SGD）等等。实际上，这些优化算法在当前最火热的深度学习中也占据着一席之地，例如adagrad、RMSprop，Adam等等。而本文则将主要介绍一下随机梯度下降法。
随机梯度下降法主要是用来解决求和形式的优化问题，与上面需要优化的目标函数一致。其思想也很简单，既然对于求和式中每一项求梯度很麻烦，那么干脆就随机选其中一项计算梯度当作总的梯度来使用好了。
具体应用到上文中的目标函数：
SSE是关于P和Q的多元函数，当随机选定U和I之后，需要枚举所有的k，并且对以及求偏导数。整个式子中仅有这一项与之相关，通过链式法则可知：
在实际的运算中，为了P和Q中所有的值都能得到更新，一般是按照在线学习的方式选择评分矩阵中有分数的点对应的U、I来进行迭代。
值得一提的是，上面所说的各种优化都无法保证一定能找到最优解。有论文指出，单纯判断驻点是否是局部最优解就是一个NPC问题，但是也有论文指出SGD的解能大概率接近局部最优甚至全局最优。
另外，相比于利用了黑塞矩阵的牛顿迭代法，梯度下降法在方向上的选择也不是最优的。牛顿法相当于考虑了梯度的梯度，所以相对更快。而由于其线性逼近的特性，梯度下降法在极值点附近可能出现震荡，相比之下牛顿法就没有这个问题。但是在实际应用中，计算黑塞矩阵的代价是非常大的，在这里梯度下降法的优势就凸显出来了。因此，牛顿法往往应用于一些较为简单的模型，如逻辑回归。而对于稍微复杂一些的模型，梯度下降法及其各种进化版本则更受青睐。
3、基于FunkSVD的改进算法
到这一步为止，我们已经能通过SGD找到一组分解方案了，然而对于填充矩阵的FunkSVD算法本身而言，目前这个形式是否过于简单了一些呢？
实际上，在FunkSVD被提出之后，出现了一大批改进算法。本文将介绍其中某些经典的改进思路。
1）正则化
对于所有机器学习算法而言，过拟合一直是需要重视的一个问题，而加入正则化项则是防止过拟合的经典处理方法。对于上面的FunkSVD算法而言，具体做法就是在损失函数后面加入一个L2正则项，即：
其中，λ为正则化系数，而整个求解过程依然可以使用随机梯度下降来完成。
2）偏置
考察式子：
可以发现这个式子表明用户U对物品I的评分全部是由U和I之间的联系带来的，然而实际上，有很多性质是用户或者物品所独有的。比如某个用户非常严苛，不论对什么物品给出的分数都很低，这仅仅与用户自身有关。又比如某个物品非常精美，所有用户都会给出较高的分数，这也仅仅与物品自身有关。因此，只通过用户与物品之间的联系来预测评分是不合理的，同时也需要考虑到用户和物品自身的属性。于是，评分预测的公式也需要进行修正。不妨设整个评分矩阵的平均分为σ，用户U和物品I的偏置分别为bU和bI，那么此时的评分计算方法就变成了：
同时，误差E除了由于M‘计算方式带来的变化之外，也同样需要加入U和I偏置的正则项，因此最终的误差函数变成了：
3）隐式反馈
对于实际的应用场景中，经常有这样一种情况：用户点击查看了某一个物品，但是最终没有给出评分。实际上，对于用户点击查看物品这个行为，排除误操作的情况，在其余的情况下可以认为用户被物品的描述，例如贴图或者文字描述等所吸引。这些信息我们称之为隐式反馈。事实上，一个推荐系统中有明确评分的数据是很少的，这类隐式数据才占了大头。
可以发现，在我们上面的算法当中，并没有运用到这部分数据。于是对于评分的方法，我们可以在显式兴趣+偏置的基础上再添加隐式兴趣，即：
其中N(U)表示为用户U提供了隐式反馈的物品的集合。这就是svd++算法。
此时的损失函数也同样需要加上隐式兴趣的正则项，即：
4）对偶算法
在上面的svd++中，我们是基于用户角度来考虑问题的，很明显我们同样可以基于物品的角度来考虑问题。具体来说就是：
其中 N(I)表示为物品I提供了隐式反馈的用户的集合。类似地，在损失函数中也需要加上隐式兴趣的正则项。
在实际运用中，可以将原始的svd++得到的结果与对偶算法得到的结果进行融合，使得预测更加准确。然而相比起物品的数目，用户的数目往往是要高出几个量级的，因此对偶算法在储存空间和运算时间的开销上都将远高于原始的svd++，如何在效率和准确度之间找到平衡也是一个需要思考的问题。
4、因子分解机
矩阵分解的思想除了直接应用在分解评分矩阵上之外，其思想也能用在其他地方，接下来介绍的因子分解机（Factorization Machine，FM）就是一个例子。
对于经典的逻辑回归算法，其sigmoid函数中的项实际上是一个线性回归：
在这里我们认为各个特征之间是相互独立的，而事实上往往有些特征之间是相互关联、相互影响的。因此，就有必要想办法捕捉这些特征之间的相互影响。简单起见，先只捕捉二阶的关系，即特征之间两两之间的相互影响。具体反映到回归公式上，即为：
然而在实际场景中，数据往往是非常稀疏的，这就导致模型很难学到后面的二阶权重。受到矩阵分解技术的启发，如果把所有的二阶特征按顺序整理成一个矩阵，那么对于这个矩阵我们可以想办法将其进行矩阵分解，从而将二阶权重表示成隐向量乘积的形式。此时，回归的式子就变成了：
具体来说就是使用来描述，对于w而言，其中可学习的项就对应了评分矩阵中有分值的项，而其他由于数据稀疏导致难以学习的项就相当于评分矩阵中的未评分项。这样一来，不仅解决了数据稀疏性带来的二阶权重学习问题，同时对于参数规模，也从O(n2)级别降到了O(kn)级别。
5、与DNN的结合
深度学习无疑是近几年来最热门的机器学习技术。注意到隐语义模型中，隐含特征与深度学习中的embedding实际上是一回事，那么是否有可能借助DNN来帮助我们完成矩阵分解的工作呢？
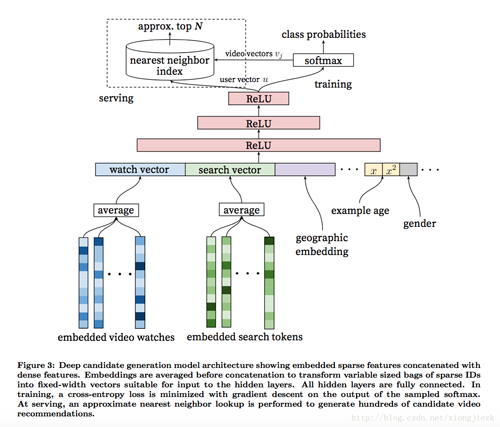
实际上，在YouTube的文章《Deep neural networks for YouTube recommendations》中，就已经有了相关技术的应用。
上图是YouTube初排模型的图示。具体的流程为首先通过nlp技术，如word2vec，预训练出所有物品的向量I表示。然后对于每一条用户对物品的点击，将用户的历史点击、历史搜索、地理位置信息等信息经过各自的embedding操作，拼接起来作为输入，经过MLP训练后得到用户的向量表示U，而最终则是通过softmax函数来校验U*I的结果是否准确。
相比于传统的矩阵分解算法，使用DNN能为模型带来非线性的部分，提高拟合能力。另一方面，还可以很方便地加入各式各样的特征，提高模型的准确度。
6、矩阵分解的优缺点
矩阵分解有如下优点：
1）能将高维的矩阵映射成两个低维矩阵的乘积，很好地解决了数据稀疏的问题。
2）具体实现和求解都很简洁，预测的精度也比较好。
3）模型的可扩展性也非常优秀，其基本思想也能广泛运用于各种场景中。
相对的，矩阵分解的缺点则有：
1）可解释性很差，其隐空间中的维度无法与现实中的概念对应起来。
2）训练速度慢，不过可以通过离线训练来弥补这个缺点。
3）实际推荐场景中往往只关心topn结果的准确性，此时考察全局的均方差显然是不准确的。
7、总结
矩阵分解作为推荐系统中的经典模型，已经经过了十几年的发展，时至今日依然被广泛应用于推荐系统当中，其基本思想更是在各式各样的模型中发挥出重要作用。但是对于推荐系统来说，仅仅有一个好的模型是远远不够的。影响推荐系统效果的因素非常之多。想要打造一个一流的推荐系统，除了一个强大的算法模型之外，更需要想方设法结合起具体业务，不断进行各种尝试、升级，方能取得最终的胜利。
作者
周颢钰，达观数据算法工程师，负责达观数据个性化推荐系统的研发与优化，研究推荐系统中的机器学习算法及其具体应用，对各种机器学习算法有浓厚兴趣。
参考文献
【1】Simon Funk, http://sifter.org/~simon/journal/20061211.html
【2】Koren, Yehuda, Robert Bell, and Chris Volinsky. "Matrix factorization techniques for recommender systems."?Computer42.8 (2009).
【3】Jahrer, Michael, and Andreas T?scher. "Collaborative filtering ensemble."?Proceedings of the 2011 International Conference on KDD Cup 2011-Volume 18. JMLR. org, 2011.
【4】Rendle, Steffen. "Factorization machines."?Data Mining (ICDM), 2010 IEEE 10th International Conference on. IEEE, 2010.
【5】Covington, Paul, Jay Adams, and Emre Sargin. "Deep neural networks for youtube recommendations."?Proceedings of the 10th ACM Conference on Recommender Systems. ACM, 2016.
“达观杯”NLP算法大赛火热开赛~ 本次大赛以文本智能处理为主题，鼓励选手用自己的智慧，结合先进的NLP人工智能技术，深入分析文本内在结构实现精准分类，万元奖金、直通Offer等你来！
【本文为51CTO专栏作者“达观数据”的原创稿件，转载可通过51CTO专栏获取联系】
