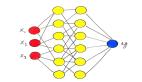
如今提及人工智能,大家期待的一定是某种可以“学习”的方法,这种方法使用数学模型从数据中获取模式的某种表示。在众多“学习”方法中,获得最多关注,承载最多期望的非“神经网络”莫属。既然我们将这种数学方法称作神经网络,那么他必然和广泛存在于生物体内的神经网络存在某种联系。让我们考察一个典型的神经连接。

每个神经元(细胞)都向外伸出许多分支,其中用来接收输入的分支称作树突(dendrities),用来输出信号的分支称作轴突(axon),轴突连接到树突上形成一个突触(synapse)。每个神经元可以通过这种方式连接多个其他神经元,每个神经元也可以接受多个其他神经元的连接。很多连接起来的神经元形成了网状结构,海量具有传感和伸缩功能的体细胞通过神经纤维连接在这个网状结构的输入和输出端,中枢神经系统正是通过这种网状结构获得了“智能”,至少是驱动机体做出了趋利避害的选择。
模式识别中的分类问题就是一种典型的选择。看起来,这给出了一种解决分类问题的启示。但是这种网状结构是怎么工作的呢?生物学家已经观察到的事实是,当有外界刺激时,网络上的某些神经元会被次第激活。神经元被激活的意思是这个神经元会向外传递信号或者对外传递的信号强度较大。
为了便于利用,需要对激活过程建立数学模型。首先将目光聚焦在一个突触上,轴突释放递质被树突吸收或者电信号从树突传递到轴突就完成了信息的传递。如何表示突触传递的信息呢?给出选择是用一个数值来表示,这寓示着将信息只归为一个类别,并用数值的大小表示其数量方面的属性。这样粗暴的简化有意义吗?实际递质可是多种多样的啊[1]!显而易见将一个轴突的输出表示成一个多维向量才是更合理的。但是我们可以引入多个虚拟突触来实现这个多维向量的各个维度的信息的传递,既然都是同样结构的突触,为何不先只考察其中一个呢。
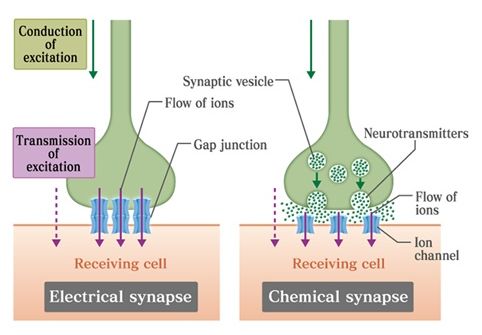
接下来考察神经元的激活。激活可以有两种模型结构——跳变式和连续式。跳变式激活方式是:引入一个阈值,当输入信息经过某种处理后大于阈值即表示激活,小于阈值表示未激活。连续式激活方式表示神经元不是只有激活和未激活两种状态,而是有不同的激活水平,输入信息经过某种处理后直接输出激活水平。同样,因为在突触中可能[几乎是确定的]同时传递了多种信息,是否应该为一个神经元提供多个激活模型呢?对这个问题解答同样是同形重复,引入虚拟神经元,让一个神经元只表示其中一个激活模型。让这个虚拟神经元接收所有树突上的输入信息,经过激活模型处理后生成一维的激活水平。什么?激活水平也应该是多维的?好办,再引入虚拟神经元,每个神经元只管生成其中某一维的激活水平。

多维变一维,显然数学模型应该是加权和,给每一维找到一个权重相乘再加起来。

但是这个模型是线性的,所有输入和输出组成的点集落在一个超平面上。是不是太简单了点,不管怎么调整这几个权重参数可以表示的情形都是平面。那么再引入一个非线性[2]函数以这个加权和为输入,将其输出作为激活水平,这个非线性函数称作激活函数。至此神经元的数学模型算是初步建立起来了。
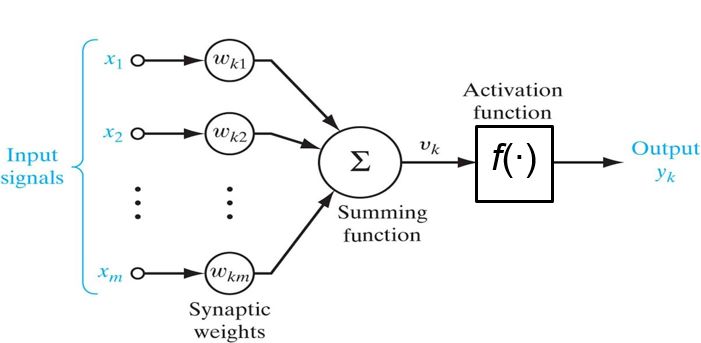
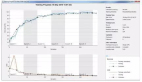
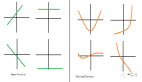
激活函数该如何选取呢?很可惜,答案是不知道。目前对生物神经网络的了解,不能给予确定激活函数的启示。不知道那么就可以随意安排,早期常用的激活函数是Sigmoid。其函数图像和公式如下。
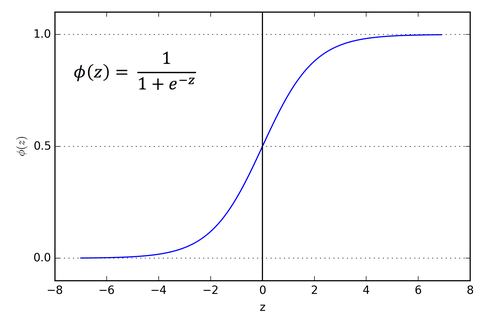
这是一个关于(0,0.5)中心对称的函数,以加权和作为输入形成的超平面总是关于(0,0.5)中心对称的,这多少让人感觉有些不安。那么在激活函数的自变量上增加一个偏移量,这个偏移量将会导致函数图像在z轴上平移。至此构成神经网络的基本元素——处理输入产生输出的神经元模型已经建立好了。
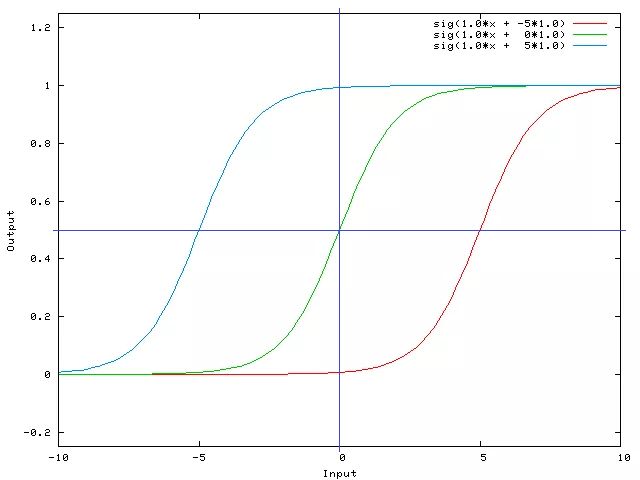
激活函数的偏移量使得超平面可以离开原点了,这仅仅是数学上的意义;其实它还完成了对跳变式激活方式的建模。参考上图,假设水平蓝线以上的数值才能表示激活,那么对于蓝色的图像来说处于持续激活状态,绿色的图片表示只要有输入就激活,而红色的部分则表示当输入数值超过5时才忽然进入激活状态,这就是跳变了。
在实际操作中对于激活函数的选取是有一定指导原则的——层数越深,激活函数越平缓。这个原则并不是来自于对神经网络模型的深入洞察,而来自于反向传播(BP)训练方法的缺陷。(对于这个缺陷我会新开一篇,并附上代码专门说明。)然而,随着对生物神经网络更进一步的了解,是否能给出更好的激活函数模型呢?答案还是不知道,甚至启示我们要放弃这种神经网络模型都是有可能的。
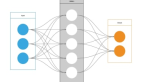
有了神经元,就可以构建网络了。在构建网络之前,先对神经元的图示结构进行简化。如下图所示,最终我们用一个圆圈表示了神经元,用带箭头的线表示了它可以接收的输入和可以产生的输出。
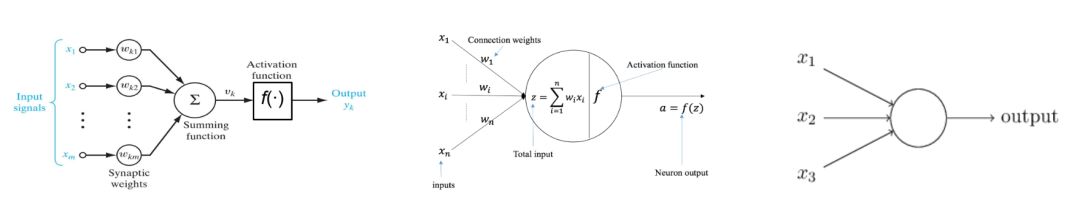
既然神经元是一个处理输入产生输出的模型,是否可以随意地把一个神经元的输出连接到另一个神经元的输入。当然可以!卷积神经网络(CNN)和回返神经网络(RNN)这两款分别在计算机视觉和自然语言处理中发挥巨大价值的神经网络结构正是源自于神经网络模型的这种灵活性。当然,这种灵活性也是“深度学习专家们”的学术灌水手段!。为了便于模型求解和编程实现,有一种简单的层状结构的构网方法。某一层的神经元仅接收且完全接受紧前层神经元的输入。采用这种原则构建出来的神经网络称作全连接神经网络。
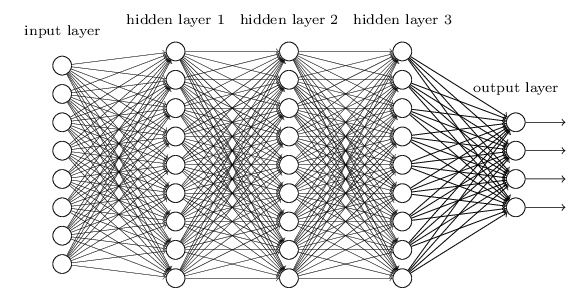
让我们回到给生物神经网络建立数学模型的目的上去——分类。怎么才能用神经网络进行分类呢?分类的数学语言描述是,找从特征空间到类别空间的映射。特征空间的确立比较简单,比如为了确定一个人是男是女,可以使用体重、身高、胸围、腰围、臀围这几个属性组成的特征空间。类别空间的确立有两种比较显然的方案。***种,只用一个维度,0表示女,1表示男。第二种,用两个维度,那个维度取值大就认为属于哪个类别,如:(1,0)表示女,(0,1)表示男。通常用第二种方案表示类别空间,***种用于解决回归问题。并没有什么特殊的原因,只是第二种比较便于建立目标函数模型(通常是损失函数)以实现***化,这也是尽量把待解决问题向分类问题上转换的原因。
让神经网络的输入层神经元的个数等于特征空间的维数,输出层神经元的个数等于类别空间的维数,中间层随意安排。然后将已知的数据带入模型,求解模型的参数。将不确定男女的(体重,身高,胸围,腰围,臀围)带入模型,求出一个解(女,男);然后判断那一维的数值大,女>男就认为输入的是女性的特征,男>女就为认为输入的是男性的特征。
[1]Bilingual neurons release glutamate and GABA
https://www.nature.com/articles/nn.3840
[2]激活函数也可以是分段线性函数