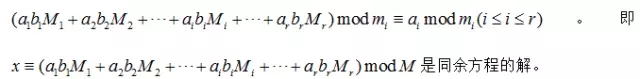谈到现代密码学,其中数论的影响举足轻重。计算机算法的实现、密码算法的构造、软硬件的优化,都离不开数论的理论支持。作为信息安全行业的工作者和学生,数论是我们无法绕开的高山,是心底无法抚平的忧伤。而中国剩余定理,算是***恨交织的那一部分吧。
遍寻信息安全的数学基础,欧几里得、欧拉、费尔马、伽罗瓦都是西域来的高山,只有中国剩余定理,那是有古籍为证的咱中国特产。怀着自豪的心去听,发现一样听不懂。感觉自己白进化了两千年……
研究中国剩余定理以前,必须要了解其对信息安全行业的应用价值,以公钥密码为例。1976年,Diffie和Hellman提出的DH密钥协商协议开创了基于数学难题的公钥密码新时代。公钥密码设计的基本思路是:寻找一个公认的数学难题,在难题的基础上构建密码算法。例如DH密钥协商算法的有效性依赖于计算离散对数的难度,使得有限域中已知明文M计算密文C简单,但已知C计算M困难。Alice与Bob为了安全通信,需要安全交换一个密钥,于是他们俩分别选择了自己的秘密a和b,g是双方已知的大素数的原根,计算Ca=g^a,Cb=g^b,得到对方的Ca和Cb后,两人分别计算Cab=Ca^b=Cb^a=g^ab,这样,Alice与Bob偷偷完成了公共密钥的协商,以后就可以加密通信啦。计算g^a,在数学家的手里就是一条公式,但真正操作起来,g和a可能是一个1024或2048位的二进制大数,我们现在的计算机CPU也不过能一次性操作64位的二进制——草稿纸都写不下的数字怎么计算连乘?没问题,中国剩余定理来帮你。
中国剩余定理原理
中国剩余定理(Chineseremaindertheorem,CRT),又称为孙子剩余定理,最早见于《孙子算经》的下卷第28题“物不知数”:
有物不知其数,三三数之剩二,五五数之有三,七七数之有二,问物几何?
大意是,这边有一堆物品不知道数量,有人三个三个地数***剩了两个,有人五个五个的数***剩了三个,有人七个七个的数***剩了两个,请问这堆物品应该是多少个?
这道题很像民间传说“韩信点兵”。秦朝末年,楚汉相争。一次,韩信与楚王大将李锋交战。苦战一场,楚军不敌,败退回营,汉军也死伤四五百人,于是韩信整顿兵马也返回大本营。当行至一山坡,忽有后军来报,说有楚军骑兵追来。只见远方尘土飞扬,杀声震天。汉军本来已十分疲惫,这时队伍大哗。韩信兵马到坡顶,见来敌不足五百骑,便急速点兵迎敌。他命令士兵3人一排,结果多出2名;接着命令士兵5人一排,结果多出3名;他又命令士兵7人一排,结果又多出2名。韩信马上向将士们宣布:我军有1073名勇士,敌人不足五百,我们居高临下,以众击寡,一定能打败敌人。于是汉军士气大振,一时间旌旗摇动,鼓声喧天,汉军步步进逼,楚军乱作一团。交战不久,楚军大败而逃。故事中韩信的点兵方法是中国剩余定理的一种实际应用了。
古人是如何描述剩余定理的呢?《孙子算经》后文给出了“物不知数”问题的剩余解法,“术曰:三三数之,剩二,置一百四十;五五数之,剩三,置六十三;七七数之,剩二,置三十。并之,得二百三十三,以二百一十减之,即得。凡三三数之,剩一,则置七十;五五数之,剩一,则置二十一;七七数之,剩一,则置十五。一百六以上,以一百五减之,即得。”“物不知数”为后来的“大衍求一术”的起源,被看作是中国数学史上最有创造性地成就之一,称为中国剩余定理。
为方便读者理解中国剩余定理,用现今的数论知识描述此定理如下[1]:
设m1,m2,…,mk是大于1的k(k≥2)个两两互素的正整数,b1,b2,…,bk∈Z,由k个一元一次同余方程联立的方程组如下:
下面以我国古代数学家杨辉在1275年所写的《续古摘奇算法》中的一道题目作为例子详解中国剩余定理求解过程。
题目:二数余一,五数余二,七数余三,九数余四,问本数。
解:由题意有
中国剩余定理历史发展演进
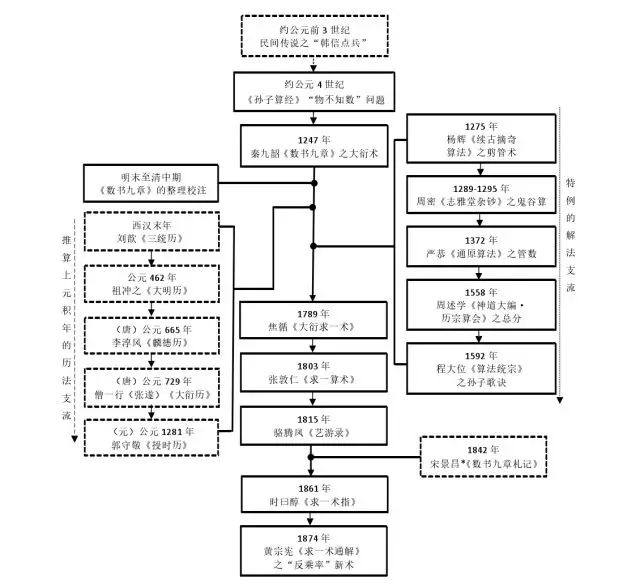
中国剩余定理历史发展演进路线如下图所示:
图1中国剩余定理历史发展演进路线简图[2]
中国剩余定理的应用
现代密码学
在现代密码学领域,RSA公钥密码体制至今仍被认可和采用,是公认的安全性良好的密码体制,也是现阶段比较常用的密码体制。而基于中国剩余定理的单基数转换法(SRC)和混合基数转换法(MRC)可以快速实现RSA的解密,解密速度大约提高四倍左右,这在无论软件还是硬件实现RSA密码算法都是非常重要的[3]。中国剩余定理还可以应用在轻量级密码设计、PKI认证系统、通信编码等等,在信息安全领域中占有非常重要的地位。
多项式
结语
在一次同余式组问题上,中国剩余定理的研究在古代远远领先于世界,可以说明中国人的数学能力是及其出众的。古人对数学的贡献是我们的宝贵财富,中国剩余定理在密码学上的应用只是其价值的部分体现,愿研究者们可以充分利用这些财富创造更多更大的荣耀。
参考文献
[1]谷利泽、杨义先.现代密码学教程[M].北京邮电大学出版社出版.2009:53
[2]邓真峥.中国剩余定理的中外历史发展比较[D].四川师范大学,2017.
[3]贺毅朝,刘建芹,陈维海.中国剩余定理在RSA解密中的应用[J].河北省科学院学报,2003,20(3):138-143.
【本文为51CTO专栏作者“中国保密协会科学技术分会”原创稿件,转载请联系原作者】