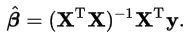说到如何用Python执行线性回归,大部分人会立刻想到用sklearn的linear_model,但事实是,Python至少有8种执行线性回归的方法,sklearn并不是***效的。
今天,让我们来谈谈线性回归。没错,作为数据科学界元老级的模型,线性回归几乎是所有数据科学家的入门必修课。抛开涉及大量数统的模型分析和检验不说,你真的就能熟练应用线性回归了么?未必!
在这篇文章中,文摘菌将介绍8种用Python实现线性回归的方法。了解了这8种方法,就能够根据不同需求,灵活选取最为高效的方法实现线性回归。
一、“宝刀不老”的线性回归
时至今日,深度学习早已成为数据科学的新宠。即便往前推10年,SVM、boosting等算法也能在准确率上完爆线性回归。
1. 为什么我们还需要线性回归呢?
一方面,线性回归所能够模拟的关系其实远不止线性关系。线性回归中的“线性”指的是系数的线性,而通过对特征的非线性变换,以及广义线性模型的推广,输出和特征之间的函数关系可以是高度非线性的。另一方面,也是更为重要的一点,线性模型的易解释性使得它在物理学、经济学、商学等领域中占据了难以取代的地位。
2. 那么,如何用Python来实现线性回归呢?
由于机器学习库scikit-learn的广泛流行,常用的方法是从该库中调用linear_model来拟合数据。虽然这可以提供机器学习的其他流水线特征(例如:数据归一化,模型系数正则化,将线性模型传递到另一个下游模型)的其他优点,但是当一个数据分析师需要快速而简便地确定回归系数(和一些基本相关统计量)时,这通常不是最快速简便的方法。
下面,我将介绍一些更快更简洁的方法,但是它们所提供信息量和建模的灵活性不尽相同。
各种线性回归方法的完整源码都可以在文末的GitHub链接中找到。他们大多数都依赖于SciPy包。
SciPy是基于Python的Numpy扩展构建的数学算法和函数的集合。通过为用户提供便于操作和可视化数据的高级命令和类,为交互式Python会话增加了强大的功能。
二、8种方法实现线性回归
方法一:Scipy.polyfit( ) or numpy.polyfit( )
这是一个最基本的最小二乘多项式拟合函数(least squares polynomial fit function),接受数据集和任何维度的多项式函数(由用户指定),并返回一组使平方误差最小的系数。这里给出函数的详细描述。对于简单的线性回归来说,可以选择1维函数。但是如果你想拟合更高维的模型,则可以从线性特征数据中构建多项式特征并拟合模型。
方法二:Stats.linregress( )
这是一个高度专业化的线性回归函数,可以在SciPy的统计模块中找到。然而因为它仅被用来优化计算两组测量数据的最小二乘回归,所以其灵活性相当受限。因此,不能使用它进行广义线性模型和多元回归拟合。但是,由于其特殊性,它是简单线性回归中最快速的方法之一。除了拟合的系数和截距项之外,它还返回基本统计量,如R2系数和标准差。
方法三:Optimize.curve_fit( )
这与Polyfit方法是一致的,但本质上更具一般性。这个强大的函数来自scipy.optimize模块,可以通过最小二乘最小化将任意的用户自定义函数拟合到数据集上。
对于简单的线性回归来说,可以只写一个线性的mx + c函数并调用这个估计函数。不言而喻,它也适用于多元回归,并返回最小二乘度量最小的函数参数数组以及协方差矩阵。
方法四:numpy.linalg.lstsq
这是通过矩阵分解计算线性方程组的最小二乘解的基本方法。来自numpy包的简便线性代数模块。在该方法中,通过计算欧几里德2-范数||b-ax||2最小化的向量x来求解等式ax = b。
该方程可能有无数解、唯一解或无解。如果a是方阵且满秩,则x(四舍五入)是方程的“精确”解。
你可以使用这个方法做一元或多元线性回归来得到计算的系数和残差。一个小诀窍是,在调用函数之前必须在x数据后加一列1来计算截距项。这被证明是更快速地解决线性回归问题的方法之一。
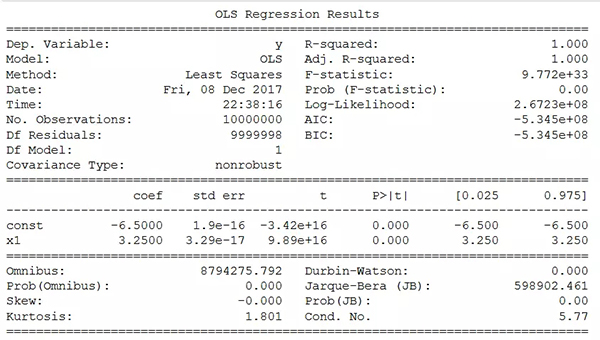
方法五:Statsmodels.OLS ( )
Statsmodels是一个小型的Python包,它为许多不同的统计模型估计提供了类和函数,还提供了用于统计测试和统计数据探索的类和函数。每个估计对应一个泛结果列表。可根据现有的统计包进行测试,从而确保统计结果的正确性。
对于线性回归,可以使用该包中的OLS或一般最小二乘函数来获得估计过程中的完整的统计信息。
一个需要牢记的小技巧是,必须手动给数据x添加一个常数来计算截距,否则默认情况下只会得到系数。以下是OLS模型的完整汇总结果的截图。结果中与R或Julia等统计语言一样具有丰富的内容。
方法六和七:使用矩阵的逆求解析解
对于条件良好的线性回归问题(其中,至少满足数据点个数>特征数量),系数求解等价于存在一个简单的闭式矩阵解,使得最小二乘最小化。由下式给出:
这里有两个选择:
- 使用简单的乘法求矩阵的逆
- 首先计算x的Moore-Penrose广义伪逆矩阵,然后与y取点积。由于第二个过程涉及奇异值分解(SVD),所以它比较慢,但是它可以很好地适用于没有良好条件的数据集。
方法八:sklearn.linear_model.LinearRegression( )
这是大多数机器学习工程师和数据科学家使用的典型方法。当然,对于现实世界中的问题,它可能被交叉验证和正则化的算法如Lasso回归和Ridge回归所取代,而不被过多使用,但是这些高级函数的核心正是这个模型本身。
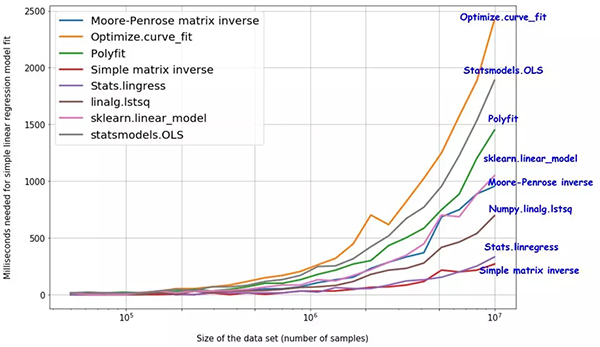
三、八种方法效率比拼
作为一名数据科学家,应该一直寻找准确且快速的方法或函数来完成数据建模工作。如果模型本来就很慢,那么会对大数据集造成执行瓶颈。
一个可以用来确定可扩展性的好办法是不断增加数据集的大小,执行模型并取所有的运行时间绘制成趋势图。
下面是源代码及其运行结果
(https://github.com/tirthajyoti/PythonMachineLearning/blob/master/Linear_Regression_Methods.ipynb)。
由于其简单,即使多达1000万个数据点,stats.linregress和简单的矩阵求逆还是最快速的方法。
四、简单矩阵逆求解的方案更快
作为数据科学家,我们必须一直探索多种解决方案来对相同的任务进行分析和建模,并为特定问题选择***方案。
在本文中,我们讨论了8种简单线性回归的方法。大多数都可以扩展到更一般化的多元和多项式回归建模中。
本文的目标主要是讨论这些方法的相对运行速度和计算复杂度。我们在一个数据量持续增加的合成数据集(最多达1000万个样本)上进行测试,并给出每种方法的运算时间。
令人惊讶的是,与广泛被使用的scikit-learnlinear_model相比,简单矩阵的逆求解的方案反而更加快速。
我们还收集了项目代码,大家可以到这里下载代码并直接运行文中提到的8种方法喔:
https://github.com/tirthajyoti/PythonMachineLearning/blob/master/Linear_Regression_Methods.ipynb
来源:
https://medium.freecodecamp.org/data-science-with-python-8-ways-to-do-linear-regression-and-measure-their-speed-b5577d75f8b
【本文是51CTO专栏机构大数据文摘的原创译文,微信公众号“大数据文摘( id: BigDataDigest)”】