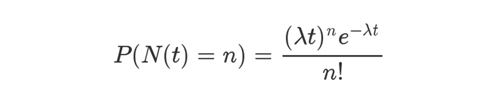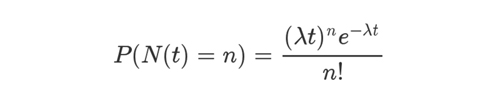常规情况下,我们一般使用多副本技术来提高存储系统的可靠性,无论是结构化数据库存储 (如典型的 mysql)、文档型 Nosql 数据库存储 (mongodb ) 或者是常规的 blob 存储系统 (GFS、Hadoop) 等,无不如此。
因为数据几乎可以称得上是企业生命力的核心,保障数据存储系统的可靠性对于任何企业来说都不是一件小事。
那么,如何较为准确地去衡量集群数据的可靠性?如何进行系统设计使得集群数据达到更高的可靠性?本文将试着去解答这些问题。
数据丢失与 copyset(复制组)
“在由 999 块磁盘组成的 3 副本存储系统中,同时坏三块盘的情况下数据丢失的概率是多大? ”,这个跟存储系统的设计息息相关,我们先考虑两个极端设计下的情况。
设计一:把 999 块磁盘组成 333 块磁盘对。
在这种设计下,只有选中其中一个磁盘对才会发生数据丢失。这种设计中,丢失数据的概率为 333/C(999,3) = 5.025095326058336*e-07。
设计二:数据随机打散到 999 块盘中。
极端情况下,随机一块盘上的逻辑数据的副本数据打散在所有集群中的 998 块盘中。这种设计下,丢失数据的概率为 C(999,3)/C(999,3)=1,也就是必然存在。
通过这两种极端的例子我们可以看到,数据的丢失概率跟数据的打散程度息息相关。为了方便后续阅读,这里我们引入一个新的概念 copyset (复制组)。
CopySet:包含一个数据的所有副本数据的设备组合,比如一份数据写入 1,2,3 三块盘,那么 {1,2,3} 就是一个复制组。
9 个磁盘的集群中,最小情况下的 copyset 的组合数为 3,copysets = {1,2,3}、{4,5,6}、{7,8,9},即一份数据的写入只能选择其中一个复制组,那么只有 {1,2,3}、{4,5,6} 或者 {7,8,9} 同时坏的情况下才会出现数据丢失。即最小 copyset 数量为 N/R。
系统中***的 copyset 的数目为 C(N,R) ,其中 R 为副本数,N 为磁盘的数量。在完全随机选择节点写入副本数据的情况下,系统中的 copyset 数目会达到***值 C(N,R)。即任意选择 R 个磁盘都会发生一部分数据的三个副本都在这 R 个盘上的情况。
磁盘数量 N,副本为 R 的存储系统中,copyset 数量 S, N/R < S < C(N, R)
磁盘故障与存储系统可靠性估算
1. 磁盘故障与柏松分布
在正式估算相关概率之前还需要科普一个基础的概率学分布:柏松分布。柏松分布主要描述在一个系统中随机事件发生的概率,譬如描述汽车站台候客人数为某个值的概率,某个医院 1 小时内出生 N 个新生儿的概率等等。
如上为泊松分布的公式。其中,P 表示概率,N 表示某种函数关系,t 表示时间,n 表示数量,λ 表示事件的频率。
举个例子:1000 块磁盘在 1 年内出现 10 块故障的概率为 P (N(365) = 10) [注:t 的平均单位为天]。λ 为 1000 块磁盘 1 天内发生故障磁盘的数量,按照 google 的统计,年故障率在 8%,那么 λ = 1000*8%/365 。
如上只是损坏 N 块磁盘概率的统计,那么怎么利用这个公式计算分布式系统中数据可靠性 (即数据丢失概率) 的近似值呢?
2. 分布式存储系统中丢失率的估算
2.1 T 时间内的故障率
对于分布式存储系统中如何进行年故障率的估算,我们先假定一种情况:T 为 1 年的情况下,系统存满数据,坏盘不处理,这种情况下统计一下数据的年故障率。
这里我们先定义一些值
N: 磁盘数量
T:统计时间
K:坏盘数量
S:系统中 copyset 数量 (复制组的个数)
R:备份数量
如何计算 T(1年)时间内数据丢失的概率,从概率统计角度来说就是把 T (1 年) 时间内所有可能出现数据丢失的事件全部考虑进去。包含 N 个磁盘 R 副本冗余的系统中,在 T 时间内可能出现数据丢失的事件,即坏盘大于等于 R 的事件,即 R,R+1,R+2,… N ( 即为 K∈[R,N] 区间所有的事件 )。这些随机事件发生时,什么情况下会造成数据丢失?没错,就是***复制组的情况下。
K 个损坏情况下 (随机选择 K 个盘情况下) ***复制组的概率为:
p = X/C(N,K) 其中 X 为随机选择 K 个磁盘过程中***复制组的组合数
那么系统出现 K 个磁盘损坏造成数据丢失的概率为:
Pa(T,K) = p * P(N(T)=K)
***系统中 T 时间内出现数据丢失的概率为所有可能出现数据丢失的事件的概率总和。
Pb(T) = Σ Pa(T,K) ; K∈[R,N]
2.2 分布式系统衡量年故障率
以上我们假设在一年中,不对任何硬件故障做恢复措施,那么 t 用一年代入即可算出此种系统状态下的年故障率。但是在大规模存储系统中,数据丢失情况下往往会启动恢复程序,恢复完了之后理论上又算是从初始状态的随机事件,加入这个因素之后计算可靠性会变得比较复杂。
理论上大规模存储系统中坏盘、恢复是极其复杂的连续事件,这里我们把这个概率模型简化为不同个单位时间 T 内的离散事件来进行统计计算。只要两个 T 之间连续事件发生的概率极小,并且 T 时间内绝大部份坏盘情况能够恢复,那么下个时间 T 就是重新从新的状态开始,则这种估算能够保证近似正确性。T 的单位定义为小时,那么 1 年可以划分为 365*24/T 个时间段,那么系统的年故障率可以理解为 100% 减去所有单位 T 时间内都不发生故障的概率。
即系统整体丢失数据的概率为:Pc = 1 - (1-Pb(T))*(36524/T)