我们先把上一期中双子表对齐例子的SQL写出来:
SELECT Orders.id, Orders.customer, A.x, B.y FROM Orders
LEFT JOIN (SELECT id,SUM(price) x FROM OrderDetail GROUP BY id ) A ON Orders.id=A.id
LEFT JOIN (SELECT id,SUM(amount) y FROM OrderPayment GROUP BY id ) B ON Orders.id=B.id
WHERE A.x > B.y
- 1.
- 2.
- 3.
- 4.
那么问题来了,这显然是个有业务意义的JOIN,它算是前面所说的哪一类呢?
这个JOIN涉及了表Orders和子查询A与B,仔细观察会发现,子查询带有GROUP BY id的子句,显然,其结果集将以id为主键。这样,JOIN涉及的三个表(子查询也算作是个临时表)的主键是相同的,它们是一对一的同维表,仍然在前述的范围内。
一
但是,这个同维表JOIN却不能用上一期说的写法简化,子查询A,B都不能省略不写。
可以简化书写的原因在于:我们假定事先知道数据结构中这些表之关联关系。用技术术语的说法,就是知道数据库的元数据(metadata)。而对于临时产生的子查询,显然不可能事先定义在元数据中了,这时候就必须明确指定要JOIN的表(子查询)。
不过,虽然JOIN的表不能省略,但关联字段总是主键,已经在GROUP BY中写过了,就没有必要再写一遍了;而且,子查询的主键总是由GROUP产生,而GROUP BY的字段一定要被选出用于做外层JOIN,也没必要在GROUP和SELECT中各写一次;并且这几个子查询涉及的子表是互相独立的,它们之间不会再有关联计算了,我们就可以把GROUP动作以及聚合式直接放到主句中,从而消除一层子查询:
SELECT Orders.id, Orders.customer, OrderDetail.SUM(price) x, OrderParyment.SUM(amount) y
FROM Orders LEFT JOIN OrderDetail GROUP BY id LEFT JOIN OrderPayment GROUP BY id
WHERE A.x > B.y
- 1.
- 2.
- 3.
二
这里的JOIN和SQL定义的JOIN运算已经差别很大,完全没有笛卡尔积的意思了。而且,也不同于SQL的JOIN运算将定义在任何两个表之间,这里的JOIN,OrderDetail和OrderPayment以及Orders都是向共同的主键id靠拢,即所有表都向某一套基准维度对齐。而由于各表的维度(主键)不同,对齐时可能会有GROUP BY,在引用该表字段时就会相应地出现聚合运算。OrderDetail和OrderPayment甚至Orders之间都不直接发生关联,在书写运算时当然就不用关心它们之间的关系,甚至不必关心另一个表是否存在。而SQL那种笛卡尔积式的JOIN则总要找一个甚至多个表来定义关联,一旦减少或修改表时就要同时考虑关联表,增大理解难度。
我们称这种JOIN称为维度对齐,它并不超出我们前面说过的三种JOIN范围,但确实在语法描述上会有不同,这里的JOIN不象SQL中是个动词,却更象个连词。而且,和前面三种基本JOIN中不会或很少发生FULL JOIN的情况不同,维度对齐的场景下FULL JOIN并不是很罕见的情况。
三
虽然我们从主子表的例子抽象出维度对齐,但这种JOIN并不要求JOIN的表是主子表(事实上从上一篇的语法可知,主子表运算还不用写这么麻烦),任何多个表都可以这么关联,而且关联字段也完全不必要是主键或主键的部分。
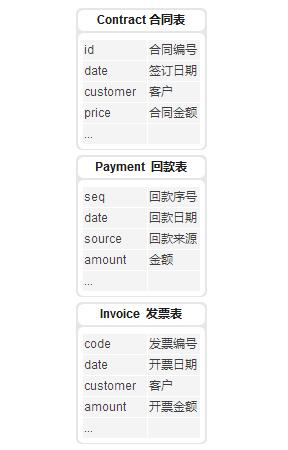
设有合同表,回款表和发票表:
现在想统计每一天的合同额、回款额以及发票额,就可以写成:
SELECT Contract.SUM(price), Payment.SUM(amount), Invoice.SUM(amount)
FROM Contract GROUP BY date FULL JOIN Payment GROUP BY date FULL JOIN Invoice GROUP BY date
- 1.
- 2.
四
这几种JOIN情况还可能混合出现。
延用上面的合同表,再有客户表和销售员表
其中Contract表中customer字段是指向Customer表的外键。
现在我们想统计每个地区的销售员数量及合同额:
SELECT Sales.COUNT(1), Contract.SUM(price)
FROM Sales GROUP BY area FULL JOIN Contract GROUP BY customer.area
- 1.
- 2.
维度对齐可以和外键属性化的写法配合合作。
五
这些例子中,最终的JOIN都是同维表。事实上,维度对齐还有主子表对齐的情况,不过相对罕见,我们将在后续仔细讲解维度概念时再涉及,上述写法中其实还有个小漏洞,有了明确的维度定义后才能将这个漏洞补上。