本质上,深度学习提供了一套技术和算法,这些技术和算法可以帮助我们对深层神经网络结构进行参数化——人工神经网络中有很多隐含层数和参数。深度学习背后的一个关键思想是从给定的数据集中提取高层次的特征。因此,深度学习的目标是克服单调乏味的特征工程任务的挑战,并帮助将传统的神经网络进行参数化。
现在,为了引入深度学习,让我们来看看一个更具体的例子,这个例子涉及多层感知器(MLP)。
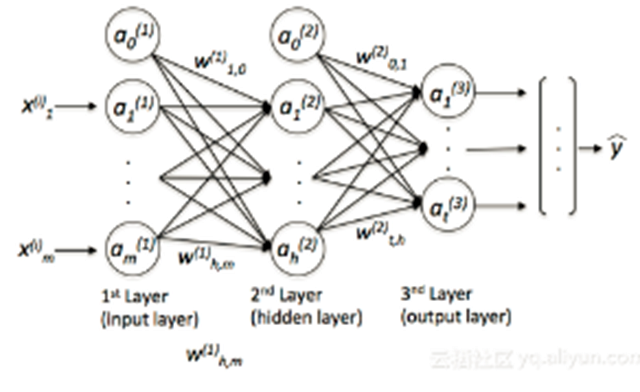
在MLP中,“感知器”这个词可能有点让人困惑,因为我们并不想只在我们的网络中使用线性神经元。利用MLP,我们可以学习复杂的函数来解决非线性问题。因此,我们的网络通常由连接输入和输出层的一个或多个“隐藏”层组成。这些隐藏的层通常有某种S型的激活函数(logs-s形或双曲正切等)。例如,在我们的网络中,一个逻辑回归单元,返回0-1范围内的连续值。一个简单的MLP看起来就像这样:
其中y是最终的类标签,我们返回的是基于输入x的预测,“a”是我们激活的神经元,而“w”是权重系数。现在,如果我们向这个MLP添加多个隐藏层,我们也会把网络称为“深度”。这种“深度”网络的问题在于,为这个网络学习“好”的权重变得越来越难。当我们开始训练我们的网络时,我们通常会将随机值赋值为初始权重,这与我们想要找到的“***”解决方案很不一样。在训练过程中,我们使用流行的反向传播算法(将其视为反向模式自动微分)来传播从右到左的“错误”,并计算每一个权重的偏导数,从而向成本(或“错误”)梯度的相反方向迈进。现在,深度神经网络的问题是所谓的“消失梯度”——我们添加的层越多,就越难“更新”我们的权重,因为信号变得越来越弱。由于我们的网络的权重在开始时可能非常糟糕(随机初始化),因此几乎不可能用反向传播来参数化一个具有“深度”的神经网络。
这就是深度学习发挥作用的地方。粗略地说,我们可以把深度学习看作是一种“聪明”的技巧或算法,可以帮助我们训练这种“深度”神经网络结构。有许多不同的神经网络结构,但是为了继续以MLP为例,让我来介绍卷积神经网络(CNN)的概念。我们可以把它看作是我们的MLP的“附加组件”,它可以帮助我们检测到我们的MLP“好”的输入。
在一般机器学习的应用中,通常有一个重点放在特征工程部分;算法学习的模型只能是和输入数据一样好。当然,我们的数据集必须要有足够多的、具有辨别能力的信息,然而,当信息被淹没在无意义的特征中,机器学习算法的性能就会受到严重影响。深度学习的目的是从杂乱的数据中自动学习;这是一种算法,它为我们提供了具有意义的深层神经网络结构,使其能够更有效地学习。我们可以把深度学习看作是自动学习“特征工程”的算法,或者我们也可以简单地称它们为“特征探测器”,它可以帮助我们克服一系列挑战,并促进神经网络的学习。
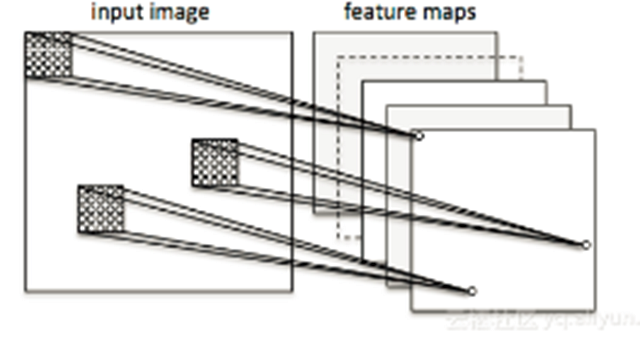
让我们在图像分类的背景下考虑一个卷积神经网络。在这里,我们使用所谓的“接收域”(将它们想象成“窗口”),它们会经过我们的图像。然后,我们将这些“接受域”(例如5×5像素的大小)和下一层的1个单元连接起来,这就是所谓的“特征图”。在这个映射之后,我们构建了一个所谓的卷积层。注意,我们的特征检测器基本上是相互复制的——它们共享相同的权重。它的想法是,如果一个特征检测器在图像的某个部分很有用,它很可能在其他地方也有用,与此同时,它还允许用不同的方式表示图像的各个部分。
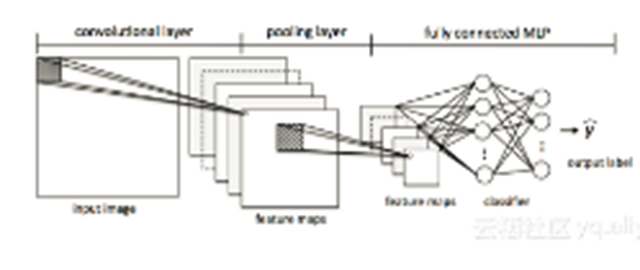
接下来,我们有一个“池”层,在这个层中,我们将我们的特征映射中的相邻特征减少为单个单元(例如,通过获取***特征,或者对其进行平均化)。我们在很多测试中都这样做,最终得出了我们的图像的几乎不不变的表示形式(确切的说法是“等变量”)。这是非常强大的,因为无论它们位于什么位置,我们都可以在图像中检测到对象。
本质上,CNN这个附加组件在我们的MLP中充当了特征提取器或过滤器。通过卷积层,我们可以从图像中提取有用的特征,通过池层,我们可以使这些特征在缩放和转换方面有一定的不同。