深入浅出解读卷积神经网络-卷积神经网络卷积核

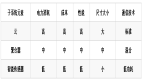
卷积神经网络

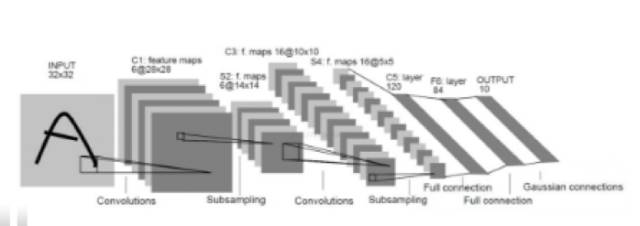
经网络结构图

图2 卷积神经网络结构图

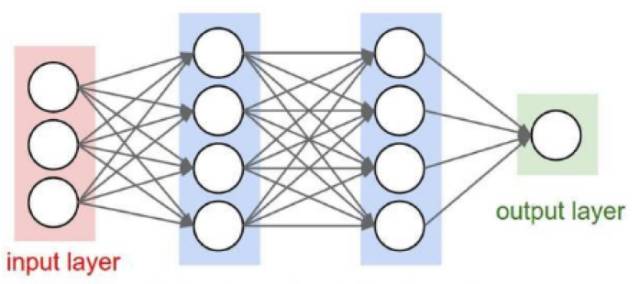
卷积神经网络和全连接的神经网络结构上的差异还是比较大的，全连接的网络，相邻两层的节点都有边相连，而卷积神经网络，相邻节点只有部分节点相连。

全连接神经网络处理图像的***问题在于全连接层的参数太多，参数太多的话容易发生过拟合而且会导致计算速度减慢，卷积神经网络可以减小参数个数的目的。

假设输入是一张图片大小为28*28*3，***层隐藏层有500个节点，那么***层的参数就有28*28*3*500+500=1176000个参数，当图片更大时，参数就更多了，而且这只是***层。

那么为什么卷积神经网络可以达到减小参数的目的呢？

卷积神经网络最为关键的有卷积层，池化层，全连接层。

卷积层

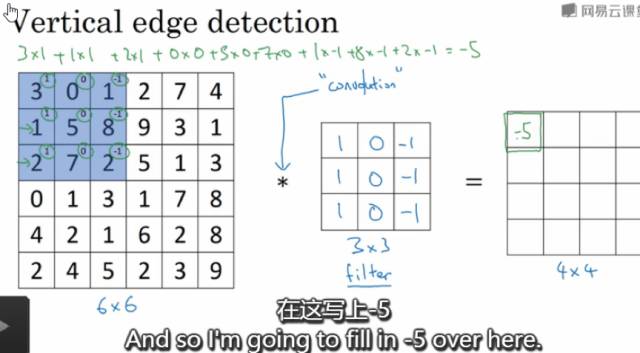
卷积层中每个节点的输入只是上一层神经网络的一小块，通常由卷积核来实现，卷积核是一个过滤器，可以想象成一个扫描窗口，扣到每张图片上，然后根据设置好的大小步长等等扫描图片，计算规则是被扣的图像像素矩阵跟卷积核的权重对应位置相乘然后求和，每扫描一次得到一个输出。卷积层所做的工作可以理解为对图像像素的每一小块进行特征抽象。可以通过多个不同的卷积核对同一张图片进行卷积，卷积核的个数，其实就是卷积之后输出矩阵的深度。卷积神经网络的参数个数与图片大小无关，只跟过滤器的尺寸、深度以及卷积核的个数（输出矩阵的深度）有关。假设是还是28*28*3的图片，卷积核的大小设为3*3*3，输出矩阵的深度为500，那么参数个数为3*3*3*500+500=14000个参数，对比全连接层，参数减少了很多。

图3 形象的卷积层示例

池化层

池化层可以认为是将一张高分辨率的图片转化为低分辨率的图片。可以非常有效的缩小矩阵的尺寸，从而减小全连接层的参数个数，这样可以加快计算速率同时又防止过拟合，池化，可以减小模型，提高速度，同时提高所提取特征的鲁棒性。

使用2*2的过滤器步长为2，***池化如下图所示：

图4 2*2过滤器***池化示例图

我们可以将卷积层和池化层看成是自动特征提取就可以了。

通过上面直观的介绍，现在我们就知道为什么卷积神经网络可以达到减小参数的目的了？

和全连接神经网络相比，卷积神经网络的优势在于共享权重和稀疏连接。共享权重在于参数只与过滤器有关。卷积神经网络减少参数的另外一个原因是稀疏连接。输出节点至于输入图片矩阵的部分像素矩阵有关，也就是跟卷积核扣上去的那一小块矩阵有关。这就是稀疏连接的概念。

卷积神经网络通过权重共享和稀疏连接来减少参数的。从而防止过度拟合。

训练过程

卷积神经网络的训练过程大致可分为如下几步：

***步：导入相关库、加载参数

import math 
import numpy as np 
import tensorflow as tf 
import matplotlib.pyplot as plt 
import h5py 
from tensorflow.python.framework import ops 
from tf_utils import * 
np.random.seed(1) 
X_train_orig,Y_train_orig,X_test_orig,Y_test_orig,classes=load_dataset() 
index=0 
plt.imshow(X_train_orig[index]) 
print("y="+str(np.squeeze(Y_train_orig[:,index]))) 
plt.show() 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.

第二步：归一化，有利于加快梯度下降

X_train=X_train_orig/255.0 
X_test=X_test_orig/255.0 
Y_train=convert_to_one_hot(Y_train_orig,6) 
Y_test=convert_to_one_hot(Y_test_orig,6) 
1.
2.
3.
4.

第三步：定义参数及卷积神经网络结构

def create_placeholder(num_px,channel,n_y): 
    X=tf.placeholder(tf.float32,shape=(None,num_px,num_px,channel),name='X') 
    Y=tf.placeholder(tf.float32,shape=(None,n_y),name='Y') 
    return X,Y 
X,Y=create_placeholder(64,3,6) 
print("X="+str(X)) 
print("Y="+str(Y)) 
 
def weight_variable(shape): 
    return tf.Variable(tf.truncated_normal(shape,stddev=0.1)) 
def bias_variable(shape): 
    return tf.Variable(tf.constant(0.1,shape=shape)) 
def conv2d(x,W): 
    return tf.nn.conv2d(x,W,strides=[1,1,1,1],padding='SAME') 
def max_pool_2x2(x): 
    return tf.nn.max_pool(x,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME') 
 
def initialize_parameters(): 
    w_conv1=weight_variable([5,5,3,32]) 
    b_conv1=bias_variable([32]) 
     
    w_conv2=weight_variable([5,5,32,64]) 
    b_conv2=bias_variable([64]) 
     
    w_fc1=weight_variable([16*16*64,512]) 
    b_fc1=bias_variable([512]) 
     
    w_fc2=weight_variable([512,6]) 
    b_fc2=bias_variable([6]) 
     
    parameters={ 
        "w_conv1":w_conv1, 
        "b_conv1":b_conv1, 
        "w_conv2":w_conv2, 
        "b_conv2":b_conv2, 
        "w_fc1":w_fc1, 
        "b_fc1":b_fc1, 
        "w_fc2":w_fc2, 
        "b_fc2":b_fc2 
    } 
    return parameters 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.

第四步：前行传播过程

def forward_propagation(X,parameters): 
    w_conv1=parameters["w_conv1"] 
    b_conv1=parameters["b_conv1"] 
    h_conv1=tf.nn.relu(conv2d(X,w_conv1)+b_conv1) 
    h_pool1=max_pool_2x2(h_conv1) 
     
    w_conv2=parameters["w_conv2"] 
    b_conv2=parameters["b_conv2"] 
    h_conv2=tf.nn.relu(conv2d(h_pool1,w_conv2)+b_conv2) 
    h_pool2=max_pool_2x2(h_conv2) 
     
    w_fc1=parameters["w_fc1"] 
    b_fc1=parameters["b_fc1"] 
    h_pool2_flat=tf.reshape(h_pool2,[-1,16*16*64]) 
    h_fc1=tf.nn.relu(tf.matmul(h_pool2_flat,w_fc1)+b_fc1) 
     
    #keep_prob=tf.placeholder(tf.float32) 
    #h_fc1_drop=tf.nn.dropout(h_fc1,keep_prob) 
     
    w_fc2=parameters["w_fc2"] 
    b_fc2=parameters["b_fc2"] 
    y_conv=tf.matmul(h_fc1,w_fc2)+b_fc2 
    return y_conv 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.

第五步：成本函数

def compute_cost(y_conv,Y): 
 
    cost=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=y_conv,labels=Y)) 
    return cost 
1.
2.
3.
4.

第六步：梯度下降更新参数

def random_mini_batches1(X, Y, mini_batch_size = 64, seed = 0): 
    m = X.shape[0]                  # number of training examples 
    mini_batches = [] 
    np.random.seed(seed) 
    Y=Y.T         #(1080,6) 
    # Step 1: Shuffle (X, Y) 
    permutation = list(np.random.permutation(m)) 
    shuffled_X = X[permutation,:,:,:] 
    shuffled_Y = Y[permutation,:].reshape((m,Y.shape[1])) 
 
    # Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case. 
    num_complete_minibatches = math.floor(m/mini_batch_size) # number of mini batches of size mini_batch_size in your partitionning 
    for k in range(0, num_complete_minibatches): 
        mini_batch_X = shuffled_X[k * mini_batch_size : k * mini_batch_size + mini_batch_size,:,:,:] 
        mini_batch_Y = shuffled_Y[k * mini_batch_size : k * mini_batch_size + mini_batch_size,:] 
        mini_batch = (mini_batch_X, mini_batch_Y) 
        mini_batches.append(mini_batch) 
     
    # Handling the end case (last mini-batch < mini_batch_size) 
    if m % mini_batch_size != 0: 
        mini_batch_X = shuffled_X[num_complete_minibatches * mini_batch_size : m,:,:,:] 
        mini_batch_Y = shuffled_Y[num_complete_minibatches * mini_batch_size : m,:] 
        mini_batch = (mini_batch_X, mini_batch_Y) 
        mini_batches.append(mini_batch) 
     
    return mini_batches 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.

第七步：训练模型

 def model(X_train,Y_train,X_test,Y_test,learning_rate=0.001,num_epochs=20,minibatch_size=32,print_cost=True):    
    ops.reset_default_graph()  #(1080, 64, 64, 3) 
    tf.set_random_seed(1)      #Y_train(6, 1080) 
    seed=3 
    (m,num_px1,num_px2,c)=X_train.shape 
    n_y=Y_train.shape[0] 
    costs=[] 
    X,Y=create_placeholder(64,3,6) 
    parameters=initialize_parameters() 
     
    Z3=forward_propagation(X,parameters) 
    cost=compute_cost(Z3,Y) 
    optm=tf.train.AdamOptimizer(learning_rate).minimize(cost) 
     
    correct_prediction=tf.equal(tf.argmax(Z3,1),tf.argmax(Y,1))#居然忘记1了，所以一直出现损失越来越小了，但是准确率却一直是0 
    accuracy=tf.reduce_mean(tf.cast(correct_prediction,tf.float32)) 
    with tf.Session() as sess: 
        tf.global_variables_initializer().run() 
        for epoch in range(num_epochs): 
            epoch_cost=0 
            num_minibatches=int(m/minibatch_size) 
            seed+=1 
            #下面输入要求（6，,1080）格式,所以要加个转置 
            minibatches=random_mini_batches1(X_train,Y_train,minibatch_size,seed) 
             
            for minibatch in minibatches: 
                (minibatch_X,minibatch_Y)=minibatch 
                _,minibatch_cost=sess.run([optm,cost],feed_dict={X:minibatch_X,Y:minibatch_Y}) 
                epoch_cost+=minibatch_cost/num_minibatches 
            if(print_cost==True and epoch % 2==0): 
                #print("Epoch",'%04d' % (epoch+1),"cost={:.9f}".format(epoch_cost)) 
                print("Cost after epoch %i:%f" % (epoch,epoch_cost)) 
            if(print_cost==True and epoch %1==0): 
                costs.append(epoch_cost) 
                 
        print("Train Accuracy:",accuracy.eval({X:X_train,Y:Y_train.T})) 
        print("Test Accuracy:",accuracy.eval({X:X_test,Y:Y_test.T})) 
        plt.plot(np.squeeze(costs)) 
        plt.ylabel('cost') 
        plt.xlabel('iterations(per tens)') 
        plt.title("learning rate="+str(learning_rate)) 
        plt.show() 
         
        parameters=sess.run(parameters) 
        return parameters 
parameters=model(X_train,Y_train,X_test,Y_test)  
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.