去年,DeepMind 的 AlphaGo 以 4-1 的比分打败了世界围棋冠军李世乭。超过 2 亿的观众就这样看着强化学习(reinforce learning)走上了世界舞台。几年前,DeepMind 制作了一个可以玩 Atari 游戏的机器人,引发轩然大波。此后这个公司很快被谷歌收购。
很多研究者相信,强化学习是我们创造通用人工智能(Artificial General Intelligence)的最佳手段。这是一个令人兴奋的领域,有着许多未解决的挑战和巨大的潜能。
强化学习起初看似非常有挑战性,但其实要入门并不困难。在这篇文章中,我们将创造一个基于 Keras 的简单机器人,使它能玩 Catch 游戏。
Catch 游戏
原始的 Catch 游戏界面
Catch 是一个非常简单的街机游戏,你可能在孩提时代玩过它。游戏规则如下:水果从屏幕的顶部落下,玩家必须用一个篮子抓住它们;每抓住一个水果,玩家得一分;每漏掉一个水果,玩家会被扣除一分。这里的目标是让电脑自己玩 Catch 游戏。不过,我们不会使用这么漂亮的游戏界面。相反,我们会使用一个简单的游戏版本来简化任务:
简化的 Catch 游戏界面
玩 Catch 游戏时,玩家要决定三种可能的行为。玩家可以将篮子左移、右移或保持不动。这个决定取决于游戏的当前状态。也就是说,取决于果子掉落的位置和篮子的位置。我们的目标是创造这样一个模型:它能在给定游戏屏幕内容的情况下,选择导致得分最高的动作。
这个任务可以被看做一个简单的分类问题。我们可以让游戏专家多次玩这个游戏,并记录他们的行为。然后,可以通过选择类似于游戏专家的「正确」动作来训练模型。
但这实际上并不是人类学习的方式。人类可以在无指导的情况下,自学像 Catch 这样的游戏。这非常有用。想象一下,你如果每次想学习像 Catch 一样简单的东西,就必须雇佣一批专家玩这个游戏上千次!这必然非常昂贵而缓慢。
而在强化学习中,模型不会根据标记的数据训练,而是通过以往的经历。
深度强化学习
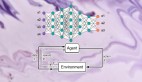
强化学习受行为心理学启发。我们并不为模型提供「正确的」行为,而是给予奖励和惩罚。该模型接受关于当前环境状态的信息(例如计算机游戏屏幕)。然后,它将输出一个动作,就像游戏手柄一样。环境将对这个动作做出回应,并提供下一个状态和奖惩行为。
据此,模型学习并寻找最大化奖励的行为。
实际上,有很多方式能够做到这一点。下面,让我们了解一下 Q-Learning。利用 Q-Learning 训练计算机玩 Atari 游戏的时候,Q-Learning 曾引起了轰动。现在,Q-Learning 依然是一个有重大意义的概念。大多数现代的强化学习算法,都是 Q-Learning 的一些改进。
理解 Q-Learning
了解 Q-Learning 的一个好方法,就是将 Catch 游戏和下象棋进行比较。
在这两种游戏中,你都会得到一个状态 S。在象棋中,这代表棋盘上棋子的位置。在 Catch 游戏中,这代表水果和篮子的位置。
然后,玩家要采取一个动作,称作 A。在象棋中,玩家要移动一个棋子。而在 Catch 游戏中,这代表着将篮子向左、向右移动,或是保持在当前位置。据此,会得到一些奖励 R 和一个新状态 S’。
Catch 游戏和象棋的一个共同点在于,奖励并不会立即出现在动作之后。
在 Catch 游戏中,只有在水果掉到篮子里或是撞到地板上时你才会获得奖励。而在象棋中,只有在整盘棋赢了或输了之后,才会获得奖励。这也就是说,奖励是稀疏分布的(sparsely distributed)。大多数时候,R 保持为零。
产生的奖励并不总是前一个动作的结果。也许,很早之前采取的某些动作才是获胜的关键。要弄清楚哪个动作对最终的奖励负责,这通常被称为信度分配问题(credit assignment problem)。
由于奖励的延迟性,优秀的象棋选手并不会仅通过最直接可见的奖励来选择他们的落子方式。相反,他们会考虑预期未来奖励(expected future reward),并据此进行选择。例如,他们不仅要考虑下一步是否能够消灭对手的一个棋子。他们也会考虑那些从长远的角度有益的行为。
在 Q-Learning 中,我们根据最高的预期未来奖励选行动。我们使用 Q 函数进行计算。这个数学函数有两个变量:游戏的当前状态和给定的动作。因此,我们可以将其记为 Q(state,action)。在 S 状态下,我们将估计每个可能的动作 A 所带来的的回报。我们假定在采取行动 A 且进入下一个状态 S’ 以后,一切都很完美。
对于给定状态 S 和动作 A,预期未来奖励 Q(S,A)被计算为即时奖励 R 加上其后的预期未来奖励 Q(S’,A’)。我们假设下一个动作 A’ 是最优的。
由于未来的不确定性,我们用 γ 因子乘以 Q(S’,A’)表示折扣:
Q(S,A) = R + γ * max Q(S’,A’)
象棋高手擅长在心里估算未来回报。换句话说,他们的 Q 函数 Q(S,A)非常精确。大多数象棋训练都是围绕着发展更好的 Q 函数进行的。玩家使用棋谱学习,从而了解特定动作如何发生,以及给定的动作有多大可能会导致胜利。但是,机器如何评估一个 Q 函数的好坏呢?这就是神经网络大展身手的地方了。
最终回归
玩游戏的时候,我们会产生很多「经历」,包括以下几个部分:
- 初始状态,S
- 采取的动作,A
- 获得的奖励,R
- 下一状态,S’
这些经历就是我们的训练数据。我们可以将估算 Q(S,A)的问题定义为回归问题。为了解决这个问题,我们可以使用神经网络。给定一个由 S 和 A 组成的输入向量,神经网络需要能预测 Q(S,A)的值等于目标:R + γ * max Q(S’,A’)。
如果我们能很好地预测不同状态 S 和不同行为 A 的 Q(S,A),我们就能很好地逼近 Q 函数。请注意,我们通过与 Q(S,A)相同的神经网络估算 Q(S’,A’)。
训练过程
给定一批经历 <S,A,R,S’>,其训练过程如下:
- 对于每个可能的动作 A’(向左、向右、不动),使用神经网络预测预期未来奖励 Q(S’,A’);
- 选择 3 个预期未来奖励中的最大值,作为 max Q(S’,A’);
- 计算 r + γ * max Q(S’,A’),这就是神经网络的目标值;
- 使用损失函数(loss function)训练神经网络。损失函数可以计算预测值离目标值的距离。此处,我们使用 0.5 * (predicted_Q(S,A)—target)² 作为损失函数。
在游戏过程中,所有的经历都会被存储在回放存储器(replay memory)中。这就像一个存储 <S,A,R,S’> 对的简单缓存。这些经历回放类同样能用于准备训练数据。让我们看看下面的代码:
- class ExperienceReplay(object):
- """
- During gameplay all the experiences < s, a, r, s’ > are stored in a replay memory.
- In training, batches of randomly drawn experiences are used to generate the input and target for training.
- """
- def __init__(self, max_memory=100, discount=.9):
- """
- Setup
- max_memory: the maximum number of experiences we want to store
- memory: a list of experiences
- discount: the discount factor for future experience
- In the memory the information whether the game ended at the state is stored seperately in a nested array
- [...
- [experience, game_over]
- [experience, game_over]
- ...]
- """
- self.max_memory = max_memory
- self.memory = list()
- self.discount = discount
- def remember(self, states, game_over):
- #Save a state to memory
- self.memory.append([states, game_over])
- #We don't want to store infinite memories, so if we have too many, we just delete the oldest one
- if len(self.memory) > self.max_memory:
- del self.memory[0]
- def get_batch(self, model, batch_size=10):
- #How many experiences do we have?
- len_memory = len(self.memory)
- #Calculate the number of actions that can possibly be taken in the game
- num_actions = model.output_shape[-1]
- #Dimensions of the game field
- env_dim = self.memory[0][0][0].shape[1]
- #We want to return an input and target vector with inputs from an observed state...
- inputs = np.zeros((min(len_memory, batch_size), env_dim))
- #...and the target r + gamma * max Q(s’,a’)
- #Note that our target is a matrix, with possible fields not only for the action taken but also
- #for the other possible actions. The actions not take the same value as the prediction to not affect them
- targets = np.zeros((inputs.shape[0], num_actions))
- #We draw states to learn from randomly
- for i, idx in enumerate(np.random.randint(0, len_memory,
- size=inputs.shape[0])):
- """
- Here we load one transition <s, a, r, s’> from memory
- state_t: initial state s
- action_t: action taken a
- reward_t: reward earned r
- state_tp1: the state that followed s’
- """
- state_t, action_t, reward_t, state_tp1 = self.memory[idx][0]
- #We also need to know whether the game ended at this state
- game_over = self.memory[idx][1]
- #add the state s to the input
- inputs[i:i+1] = state_t
- # First we fill the target values with the predictions of the model.
- # They will not be affected by training (since the training loss for them is 0)
- targets[i] = model.predict(state_t)[0]
- """
- If the game ended, the expected reward Q(s,a) should be the final reward r.
- Otherwise the target value is r + gamma * max Q(s’,a’)
- """
- # Here Q_sa is max_a'Q(s', a')
- Q_sa = np.max(model.predict(state_tp1)[0])
- #if the game ended, the reward is the final reward
- if game_over: # if game_over is True
- targets[i, action_t] = reward_t
- else:
- # r + gamma * max Q(s’,a’)
- targets[i, action_t] = reward_t + self.discount * Q_sa
- return inputs, targets
定义模型
现在让我们定义这个利用 Q-Learning 学习 Catch 游戏的模型。我们使用 Keras 作为 Tensorflow 的前端。我们的基准模型是一个简单的三层密集网络。这个模型在简单版的 Catch 游戏当中表现很好。你可以在 GitHub 中找到它的完整实现过程。
你也可以尝试更加复杂的模型,测试其能否获得更好的性能。
- num_actions = 3 # [move_left, stay, move_right]
- hidden_size = 100 # Size of the hidden layers
- grid_size = 10 # Size of the playing field
- def baseline_model(grid_size,num_actions,hidden_size):
- #seting up the model with keras
- model = Sequential()
- model.add(Dense(hidden_size, input_shape=(grid_size**2,), activation='relu'))
- model.add(Dense(hidden_size, activation='relu'))
- model.add(Dense(num_actions))
- model.compile(sgd(lr=.1), "mse")
- return model
探索
Q-Learning 的最后一种成分是探索。日常生活的经验告诉我们,有时候你得做点奇怪的事情或是随机的手段,才能发现是否有比日常动作更好的东西。
Q-Learning 也是如此。总是做最好的选择,意味着你可能会错过一些从未探索的道路。为了避免这种情况,学习者有时会添加一个随机项,而未必总是用最好的。我们可以将定义训练方法如下:
- def train(model,epochs):
- # Train
- #Reseting the win counter
- win_cnt = 0
- # We want to keep track of the progress of the AI over time, so we save its win count history
- win_hist = []
- #Epochs is the number of games we play
- for e in range(epochs):
- loss = 0.
- #Resetting the game
- env.reset()
- game_over = False
- # get initial input
- input_t = env.observe()
- while not game_over:
- #The learner is acting on the last observed game screen
- #input_t is a vector containing representing the game screen
- input_tm1 = input_t
- #Take a random action with probability epsilon
- if np.random.rand() <= epsilon:
- #Eat something random from the menu
- action = np.random.randint(0, num_actions, size=1)
- else:
- #Choose yourself
- #q contains the expected rewards for the actions
- q = model.predict(input_tm1)
- #We pick the action with the highest expected reward
- action = np.argmax(q[0])
- # apply action, get rewards and new state
- input_t, reward, game_over = env.act(action)
- #If we managed to catch the fruit we add 1 to our win counter
- if reward == 1:
- win_cnt += 1
- #Uncomment this to render the game here
- #display_screen(action,3000,inputs[0])
- """
- The experiences < s, a, r, s’ > we make during gameplay are our training data.
- Here we first save the last experience, and then load a batch of experiences to train our model
- """
- # store experience
- exp_replay.remember([input_tm1, action, reward, input_t], game_over)
- # Load batch of experiences
- inputs, targets = exp_replay.get_batch(model, batch_size=batch_size)
- # train model on experiences
- batch_loss = model.train_on_batch(inputs, targets)
- #sum up loss over all batches in an epoch
- loss += batch_loss
- win_hist.append(win_cnt)
- return win_hist
我将这个游戏机器人训练了 5000 个 epoch,结果表现得很不错!
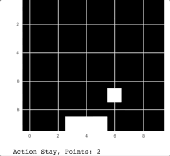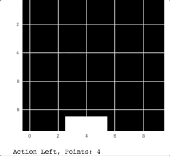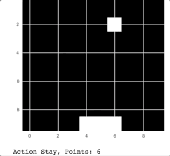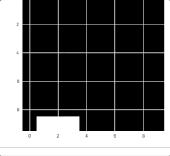
Catch 机器人的动作
正如你在上述动图中看到的那样,机器人可以抓住从天空中掉落的苹果。为了将这个模型学习的过程可视化,我绘制了每一个 epoch 的胜利移动平均线,结果如下: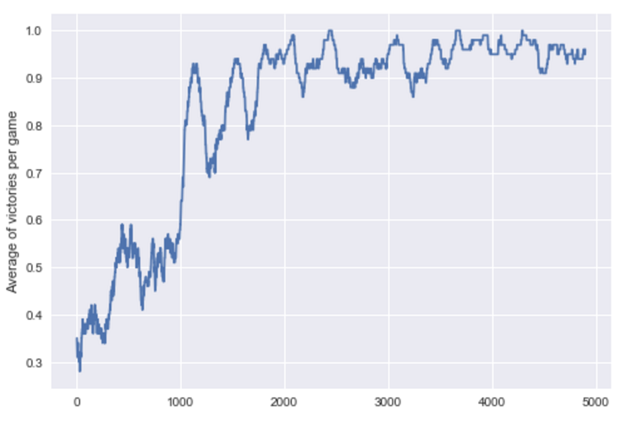
接下来做什么?现在,你已经对强化学习有了初步的直觉了解。我建议仔细阅读该教程的完整代码。你也可以试验看看。