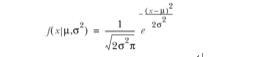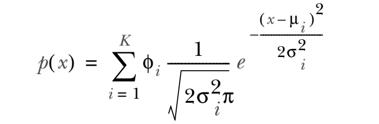本文用生动的案例对高斯混合模型原理进行了通俗易懂的讲解,并分析了高斯混合模型与另一种常见聚类算法K-means的关系。
什么是高斯混合模型(Gaussian Mixture Model)
高斯混合模型(Gaussian Mixture Model)通常简称GMM是一种业界广泛使用的聚类算法,该方法使用了高斯分布作为参数模型,并使用了期望***(Expectation Maximization,简称EM)算法进行训练。本文对该方法的原理进行了通俗易懂的讲解,期望对读者更直观的理解方法原理有帮助。文本的***还分析了高斯混合模型了另一种常见聚类算法K-means的关系,实际上在特定约束条件下,K-means算法可以被看作是高斯混合模型(GMM)的一种特殊形式。
1. 什么是高斯分布?
高斯分布(Gaussian distribution)有时也被称为正态分布(normal distribution),是一种在自然界大量存在的、最为常见的分布形式,在提供精确数学定义前,先用一个简单的例子来说明。
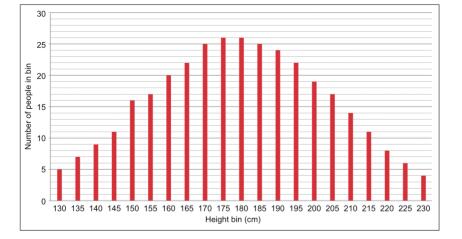
如果我们对大量的人口进行身高数据的随机采样,并且将采得的身高数据画成柱状图,将会得到如下图1所示的图形。这张图模拟展示了334个成人的统计数据,可以看出图中最多出现的身高在180cm左右2.5cm的区间里。
图1:由334个人的身高数据构成的正态分布直方图
这个图形非常直观的展示了高斯分布的形态。接下来看下严格的高斯公式定义,高斯分布的概率密度函数公式如下:
公式中包含两个参数,参数μ表示均值,参数σ表示标准差,均值对应正态分布的中间位置,在本例中我们可以推测均值在180cm附近。标准差衡量了数据围绕均值分散的程度。
学过大学高数的同学应该还记得,正态分布的一个背景知识点是,95%的数据分布在均值周围2个标准差的范围内。本例中大约20到30左右是标准差参数的取值,因为大多数数据都分布在120cm到240cm之间。
上面的公式是概率密度函数,也就是在已知参数的情况下,输入变量指x,可以获得相对应的概率密度。还要注意一件事,就是在实际使用前,概率分布要先进行归一化,也就是说曲线下面的面积之和需要为1,这样才能确保返回的概率密度在允许的取值范围内。
如果需要计算指定区间内的分布概率,则可以计算在区间首尾两个取值之间的面积的大小。另外除了直接计算面积,还可以用更简便的方法来获得同样的结果,就是减去区间x对应的累积密度函数(cumulative density function,CDF)。因为CDF表示的是数值小于等于x的分布概率。
现在我们回到之前的例子来评估下参数和对应的实际数据。假设我们用柱状线来表示分布概率,每个柱状线指相应身高值在334个人中的分布概率,用每个身高值对应的人数除以总数(334)就可以得到对应概率值,图2用左侧的红色线(Sample Probability)来表示。
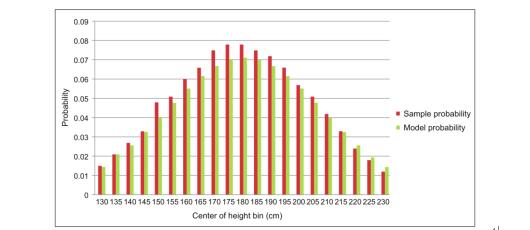
如果我们设置参数μ=180,σ=28,使用累积密度函数来计算对应的概率值——右侧绿色线(Model Probability),可以肉眼观察到模型拟合的精度。
图2
图2:对给定用户,身高分布的采样概率用红色柱状图表示,高斯模型在参数μ=180,σ=28时计算出的概率用绿色柱状图表示
观察图2可以看出,刚才咱们猜测的均值参数180和标准差参数28拟合的效果很不错,虽然可能稍微偏小了一点点。当然我们可以不断调校参数来拟合的更好些,但是更准确的办法是通过算法来生成它们,这个过程就被称为模型训练(model training)。最常用的方法是期望***(EM)算法,待会给大家详细讲解。
顺便说一句,采样的数据和全体数据的分布情况总是存在一定差异的。这里首先假设了采集的334个用户的数据能代表全体人口的身高分布。另外我们还假定了隐含的数据分布是高斯分布,并以此来绘制分布曲线,并以此为前提预估潜在的分布情况。如果采集越来越多的数据,通常身高的分布越来越趋近于高斯(尽管仍然有其他不确定因素),模型训练的目的就是在这些假设前提下尽可能降低不确定性。
2. 期望***与高斯模型训练
模型的EM训练过程,直观的来讲是这样:我们通过观察采样的概率值和模型概率值的接近程度,来判断一个模型是否拟合良好。然后通过调整模型以让新模型更适配采样的概率值。反复迭代这个过程很多次,直到两个概率值非常接近时,我们停止更新并完成模型训练。
现在我们要将这个过程用算法来实现,所使用的方法是模型生成的数据来决定似然值,即通过模型来计算数据的期望值。通过更新参数μ和σ来让期望值***化。这个过程可以不断迭代直到两次迭代中生成的参数变化非常小为止。该过程和k-means的算法训练过程很相似(k-means不断更新类中心来让结果***化),只不过在这里的高斯模型中,我们需要同时更新两个参数:分布的均值和标准差
3. 高斯混合模型(GMM)
高斯混合模型是对高斯模型进行简单的扩展,GMM使用多个高斯分布的组合来刻画数据分布。
举个具体例子来给大家说明:想象下现在咱们不再考察全部用户的身高,而是要在模型中同时考虑男性和女性的身高。假定之前的样本里男女都有,那么之前所画的高斯分布其实是两个高斯分布的叠加的结果。相比只使用一个高斯来建模,现在我们可以用两个(或多个)高斯分布:
该公式和之前的公式非常相似,细节上有几点差异。首先分布概率是K个高斯分布的和,每个高斯分布有属于自己的μ和σ参数,以及对应的权重参数 ,权重值必须为正数,所有权重的和必须等于1,以确保公式给出数值是合理的概率密度值。换句话说,如果我们把该公式对应的输入空间合并起来,结果将等于1。
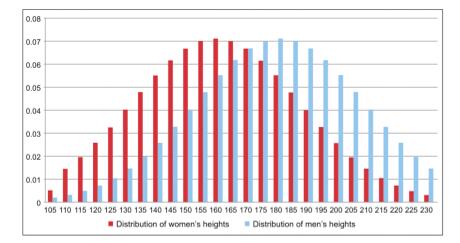
回到之前的例子,女性在身高分布上通常要比男性矮,如图3所示:
图3:男性和女性身高的概率分布图
图3的y-轴所示的概率值,是在已知每个用户性别的前提下计算出来的。但通常情况下我们并不能掌握这个信息(也许在采集数据时没记录),因此不仅要学出每种分布的参数,还需要生成性别的划分情况( )。当决定期望值时,需要将权重值分别生成男性和女性的相应身高概率值并相加。
注意虽然现在模型更复杂了,但仍然可使用与之前相同的技术进行模型训练。在计算期望值时(很可能通过已被混合的数据生成),只需要一个更新参数的***化期望策略。
4. 高斯混合模型的学习实例
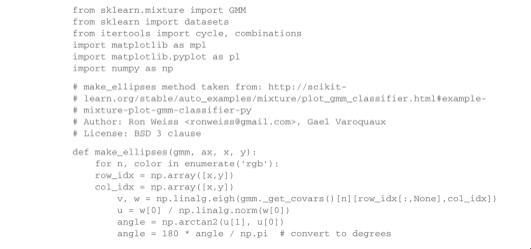
前面的简单例子里使用了一维高斯模型:即只有一个特征(身高)。但高斯不仅局限于一维,很容易将均值扩展为向量,标准差扩展为协方差矩阵,用n-维高斯分布来描述多维特征。接下来的程序清单里展示了通过scikit-learn的高斯混合模型运行聚类并对结果进行可视化展示。
在初始化GMM算法时,传入了以下参数:
- -n_components ——用户混合的高斯分布的数量。之前的例子里是2个。
- -covariance_type ——约定协方差矩阵的属性,即高斯分布的形状。参考下面文档来具体了解:http://scikit-learn.org/stable/modules/mixture.html
- -n_iter —— EM的迭代运行次数。
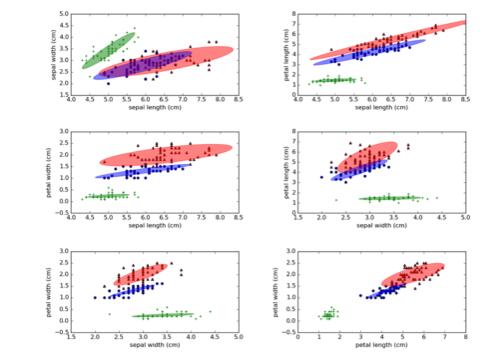
计算结果如下图(Iris数据集):
- 有关make_ellipses ——make_ellipses来源于plot_gmm_classifier方法,作者为scikit-learn的Ron Weiss和Gael Varoquaz。根据协方差矩阵绘制的二维图形,可以找出方差***和其次大的坐标方向,以及相对应的量级。然后使用这些坐标轴将相应的高斯分布的椭圆图形绘制出来。这些轴方向和量级分别被称为特征向量(eigenvectors)和特征值(eigenvalues)。
图4:展示了Iris数据集的4-D高斯聚类结果在二维空间上的映射图
make_ellipses方法在概念上很简单,它将gmm对象(训练模型)、坐标轴、以及x和y坐标索引作为参数,运行后基于指定的坐标轴绘制出相应的椭圆图形。
5. k-means和GMM的关系
在特定条件下,k-means和GMM方法可以互相用对方的思想来表达。在k-means中,根据距离每个点最接近的类中心来标记该点的类别,这里存在的假设是每个类簇的尺度接近且特征的分布不存在不均匀性。这也解释了为什么在使用k-means前对数据进行归一会有效果。高斯混合模型则不会受到这个约束,因为它对每个类簇分别考察特征的协方差模型。
K-means算法可以被视为高斯混合模型(GMM)的一种特殊形式。整体上看,高斯混合模型能提供更强的描述能力,因为聚类时数据点的从属关系不仅与近邻相关,还会依赖于类簇的形状。n维高斯分布的形状由每个类簇的协方差来决定。在协方差矩阵上添加特定的约束条件后,可能会通过GMM和k-means得到相同的结果。
实践中如果每个类簇的协方差矩阵绑定在一起(就是说它们完全相同),并且矩阵对角线上的协方差数值保持相同,其他数值则全部为0,这样能够生成具有相同尺寸且形状为圆形类簇。在此条件下,每个点都始终属于最近的中间点对应的类。
在k-means方法中,使用EM来训练高斯混合模型时对初始值的设置非常敏感。而对比k-means,GMM方法有更多的初始条件要设置。实践中不仅初始类中心要指定,而且协方差矩阵和混合权重也要设置。这里可以运行k-means来生成类中心,并以此作为高斯混合模型的初始条件。由此可见两个算法有相似的处理过程,主要区别在于模型的复杂度不同。
整体来看,所有无监督机器学习算法都遵循一条简单的模式:给定一系列数据,训练出一个能描述这些数据规律的模型(并期望潜在过程能生成数据)。训练过程通常要反复迭代,直到无法再优化参数获得更贴合数据的模型为止。
【本文为51CTO专栏作者“达观数据”的原创稿件,转载可通过51CTO专栏获取联系】