当你刚开始学习编程的时候,将数组作为“主要数据结构”来学习是很常见的。
最终,你也会学习到哈希表。如果你正在攻读计算机科学学位,你肯定需要参加一门数据结构的课程。在课上你将会学到邻接链表、队列和栈。这些数据结构都被称作是“线性”的,因为他们都有逻辑上的起点和终点。
当我们开始学习树和图的时候,这两个数据结构确实会让人困惑,因为它们存储数据不是线性方式了。这两种数据结构都用特定的方式存储数据。
这篇文章帮助你更好的理解树形数据结构并帮你弄清楚你对它的疑问。
本篇文章我们将会学习到:
- 树是什么?
- 树的例子
- 树的术语及其工作原理
- 如何用代码实现树形结构
让我们开始学习之旅吧。:)
定义
当开始编程时,人们更容易理解线性数据结构,而不是像树和图这样的数据结构。
树是众所周知的非线性数据结构。它们不以线性方式存储数据,而是按层次组织数据。
让我们举个现实生活中的例子
当我说层次方式意味着什么?
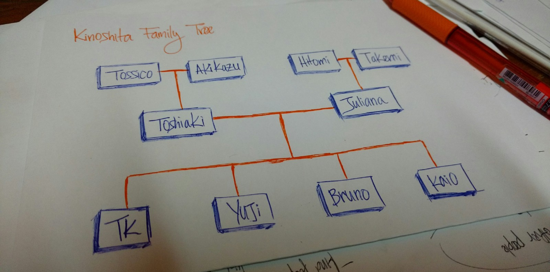
想象一个有所有辈分关系的家谱:祖父母、父母、子女、兄弟姐妹们等等。我们通常按层次结构组织家谱。
上面的图是我的家谱。Tossico 、Akikazu 、Hitomi 和 Takemi 是我的祖父母。
Toshiaki 和 Juliana 是我的父母。
TK 、Yuji 、Bruno 和 Kaio 是我父母的孩子(我和我的兄弟们)。
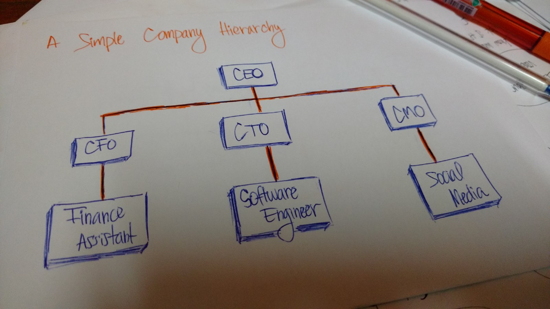
另一个层次结构的例子是企业的组织结构。
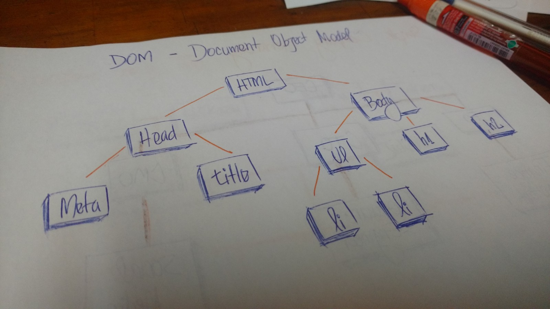
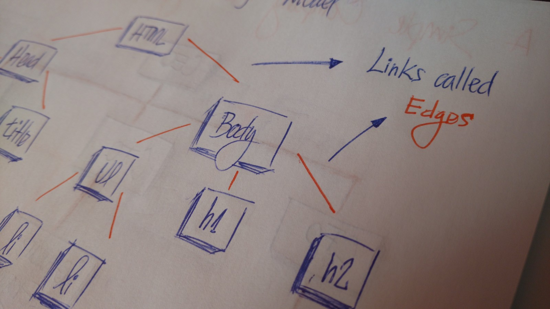
在 HTML 中,文档对象模型(DOM)是树形结构的。
HTML 标签包含其他的标签。我们有一个 head 标签和 body 标签。这些标签包含特点的元素。head 标签中有 meta 和 title 标签。body 标签中有在用户界面展示的标签,如 h1 、a 、li 等等。
术语定义
树是被称为节点的元素的集合。节点通过边连接。每个节点都有一个值或数据。每个节点也可能有或者没有子节点。
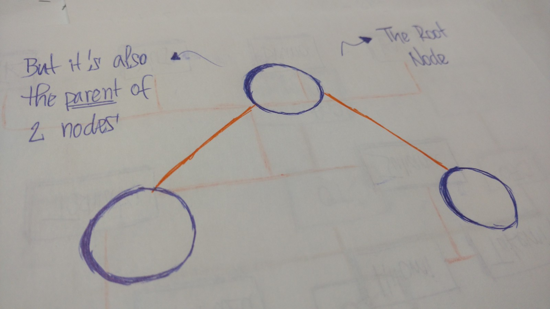
树的首节点是这个树的根(root)节点。如果这个根节点连接了另一个节点,那么,另一个节点称作这个节点的子节点。
所有树节点都由边连接。它是树的重要组成部分, 因为它管理节点之间的关系。
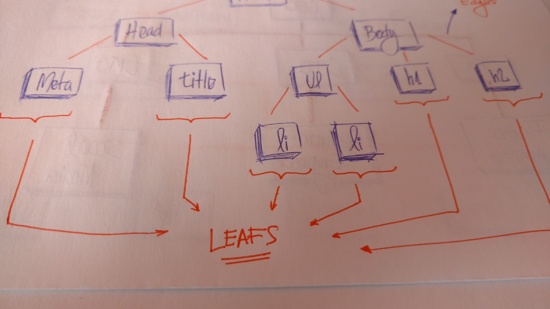
叶节点是树上的***一个节点。他们是没有子节点的节点。数据结构中的树像真正的树, 有根, 树枝, 和叶子。
要理解的其他重要概念是树的高度和深度。
- 树的高度是叶节点的最长路径的长度。
- 节点的深度是从其到根的路径的长度。
术语摘要
- 根是树的最顶端结点。
- 边是两个结点之间的连接。
- 子结点是具有父节点的结点。
- 父结点是与子节点有连接的结点。
- 叶子结点是树中没有子结点的结点。
- 高度是 树 到叶子结点的长度。
- 深度是 结点 到根结点的长度。
二叉树
现在我们来讨论一个特殊的树类型。我们把它叫作二叉树。
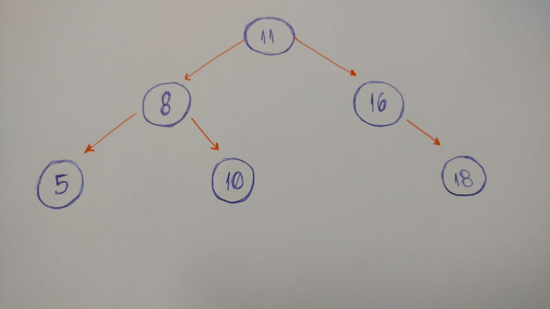
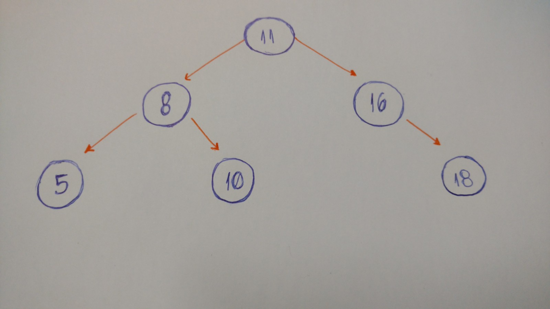
“在计算机科学领域,二叉树是一种树形数据结构,它的每个节点最多有两个孩子,被叫作左孩子和右孩”
我们来看一个二叉树的例子。
我们来写一个二叉树
在实现一个二叉树时,我们首先要注意的是,二叉树是节点的集合。每一个节点有三个属性:值(value), 左孩子( left_child) ,以及右孩子( right_child)。
那么我们怎么才能实现一个有这三个属性的简单二叉树呢?
- class BinaryTree:
- def __init__(self, value):
- self.value = value
- self.left_child = None
- self.right_child = None
好,这就是我们的二叉树类。
当我们实例化一个对象时,我们把值(节点的相关数据)作为参数传递给类。看上面类的左孩子和右孩子。两个都被赋值为None。
为什么?
因为当我们创建节点时,它还没有孩子,只有节点数据。
测试下代码。
- tree = BinaryTree('a')
- print(tree.value) # a
- print(tree.left_child) # None
- print(tree.right_child) # None
好了。
我们可以将字符串'a'作为值传给二叉树节点。如果将值、左孩子、右孩子输出的话,我们就可以看到这个值了。
下面开始插入部分的操作。那么我们需要做些什么工作呢?
有两个要求:
- 如果当前的节点没有左孩子,我们就创建一个新节点,然后将其设置为当前节点的左孩子。
- 如果已经有了左孩子,我们就创建一个新节点,并将其放在当前左孩子节点的位置。然后再将左孩子节点置为新节点的左孩子。
画出来就像下面这样。:)
下面是插入操作的代码:
- def insert_left(self, value):
- if self.left_child == None:
- self.left_child = BinaryTree(value)
- else:
- new_node = BinaryTree(value)
- new_node.left_child = self.left_child
- self.left_child = new_node
再次强调,如果当前节点没有左孩子,我们就创建一个新节点,并将其置为当前节点的左孩子。否则,就将新节点放在左孩子的位置,再将原左孩子置为新节点的左孩子。
同样,我们编写插入右孩子的代码。
- def insert_right(self, value):
- if self.right_child == None:
- self.right_child = BinaryTree(value)
- else:
- new_node = BinaryTree(value)
- new_node.right_child = self.right_child
- self.right_child = new_node
好了。:)
但是这还不算完成。我们得测试一下。
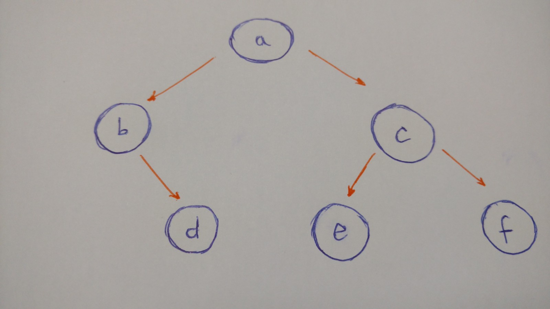
我们来构造一个像下面这样的树:
总结分析下这棵树:
- 有一个根节点
- b是左孩子
- c是右孩子
- b的右孩子是d(b没有左孩子)
- c的左孩子是e
- c的右孩子是f
- e和f都没有孩子
下面是整棵树的实现代码:
- a_node = BinaryTree('a')
- a_node.insert_left('b')
- a_node.insert_right('c')
- b_node = a_node.left_child
- b_node.insert_right('d')
- c_node = a_node.right_child
- c_node.insert_left('e')
- c_node.insert_right('f')
- d_node = b_node.right_child
- e_node = c_node.left_child
- f_node = c_node.right_child
- print(a_node.value) # a
- print(b_node.value) # b
- print(c_node.value) # c
- print(d_node.value) # d
- print(e_node.value) # e
- print(f_node.value) # f
好,插入结束。
现在,我们来思考一下树的遍历。
遍历树有两种选择:深度优先搜索(DFS)和广度优先搜索(BFS)。
- DFS是用来遍历或搜索树数据结构的算法。从根节点开始,在回溯之前沿着每一个分支尽可能远的探索。
- BFS是用来遍历或搜索树数据结构的算法。从根节点开始,在探索下一层邻居节点前,首先探索同一层的邻居节点。
下面,我们来深入了解每一种遍历算法。
深度优先搜索(Depth-First Search,DFS)
DFS 在 回溯 和搜索其他路径之前找到一条到叶节点的路径。让我们看看这种类型的遍历的示例。
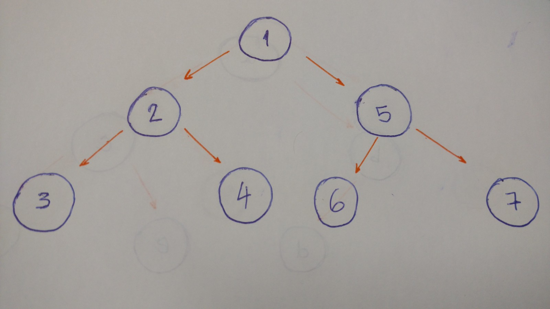
此算法的结果是 1–2–3–4–5–6–7 。
为什么呢?
让我们分解下。
- 从根节点(1)开始。输出之。
- 进入左孩子(2)。输出之。
- 然后进入左孩子(3)。输出之。(此节点无子孩子)
- 回溯,并进入右孩子(4)。输出之。(此节点无子孩子)
- 回溯到根节点,然后进入其右孩子(5)。输出之。
- 进入左孩子(6)。输出之。(此节点无子孩子)
- 回溯,并进入右孩子(7)。输出之。(此节点无子孩子)
- 完成。
当我们深入到叶节点时回溯,这就被称为 DFS 算法。
既然我们对这种遍历算法已经熟悉了,我们将讨论下 DFS 的类型:前序、中序和后序。
前序遍历
这和我们在上述示例中的作法基本类似。
- 输出节点的值。
- 进入其左孩子并输出之。当且仅当它拥有左孩子。
- 进入右孩子并输出之。当且仅当它拥有右孩子。
- def pre_order(self):
- print(self.value)
- if self.left_child:
- self.left_child.pre_order()
- if self.right_child:
- self.right_child.pre_order()
中序遍历
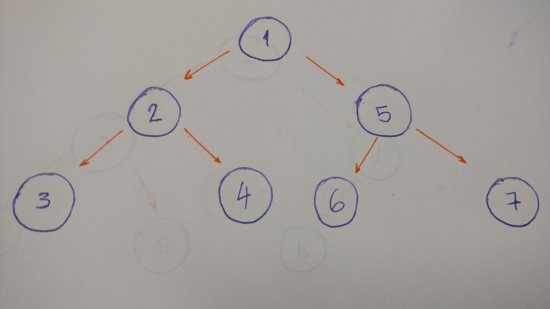
示例中此树的中序算法的结果是3–2–4–1–6–5–7。
左孩子优先,之后是中间,***是右孩子。
现在让我们编码实现之。
- def in_order(self):
- if self.left_child:
- self.left_child.in_order()
- print(self.value)
- if self.right_child:
- self.right_child.in_order()
- 进入左孩子并输出之。当且仅当它有左孩子。
- 输出节点的值。
- 进入右孩子并输出之。当且仅当它有右孩子。
后序遍历
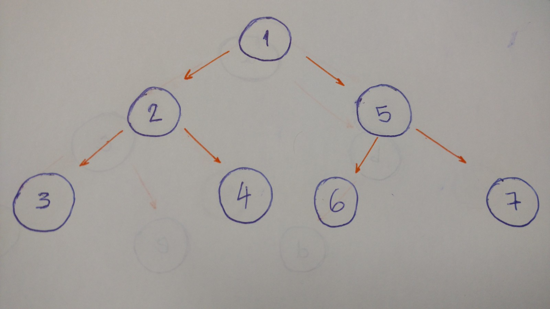
以此树为例的后序算法的结果为 3–4–2–6–7–5–1 。
左孩子优先,之后是右孩子,中间的***。
让我们编码实现吧。
- def post_order(self):
- if self.left_child:
- self.left_child.post_order()
- if self.right_child:
- self.right_child.post_order()
- print(self.value)
- 进入左孩子并输出之。这当且仅当它拥有左孩子。
- 进入右孩子并输出之。这当且仅当它拥有右孩子。
- 输出节点的值。