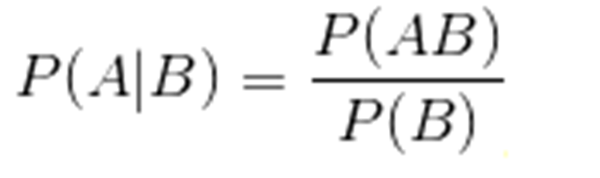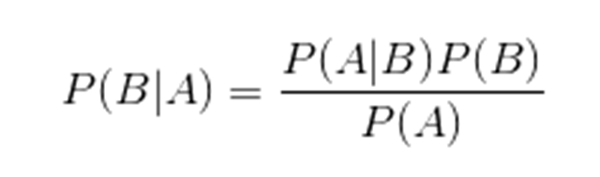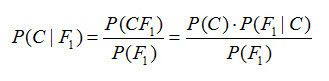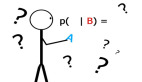做广告优化这么久了,也看过不少广告后台的受众画像,总体来说,对广告数据分析和效果优化的参考价值有限,不过聊胜于无。
究其原因,在于很多广告后台的受众画像数据,只告诉了我们看了广告的这部分人群是什么样的,而缺失了发生转化的这部分用户的画像数据。原因主要有两点:
一是在大部分广告投放过程中,前后端数据是割裂的,换句话说,媒体能知道你花钱买的广告给了谁看,但一般不知道哪些人发生了转化;而甲方通过自己的监测,可以知道转化的用户是哪一部分,如果监测做得够好,也能知道这部分的人群画像,但人群画像的判定标准与媒体方可能存在差异,统计口径不一致,数据无法人工打通。
二是媒体不愿意公开这么多的数据,甚至受众画像本身都有一定的问题。
如今信息流优化已经成为业内交流的热点,优化创意、定向等已是老生常谈,唯独受众画像的数据分析少有人提及,尚有可挖的地方。今天借此机会,和大家分享一种受众数据分析的思路。
需要强调的是,接下来的广告数据分析有一个最基本的前提:假设媒体提供的数据和甲方监测的数据都是真实准确的。下面我会以一个真实的案例和数据(今日头条,家装类)向大家介绍,如何用朴素贝叶斯的算法,对今日头条的受众画像进行数据挖掘和分析,从而实现精准定向下的转化率预测。
1.朴素贝叶斯的原理
每次提到贝叶斯定理,我心中的崇敬之情都油然而生,倒不是因为这个定理多高深,而是因为它特别有用。这个定理解决了现实生活里经常遇到的问题:已知某条件概率,如何得到两个事件交换后的概率,也就是在已知P(A|B)的情况下如何求得P(B|A)。比如,我知道发生转化的用户中,女性的比例是36%,那么当一个女性用户看到我的广告时,她有多大的可能性发生转化。
这里先解释什么是条件概率:
P(A|B)表示事件B已经发生的前提下,事件A发生的概率,叫做事件B发生下事件A的条件概率。其基本求解公式为:
贝叶斯定理之所以有用,是因为我们在生活中往往遇到这种问题:可以不费力气地直接得出P(A|B),P(B|A)则很难直接得出,但其实我们更关心P(B|A),这时候,贝叶斯定理就为我们提供了从P(A|B)获得P(B|A)的道路。
下面省略证明过程,直接给出贝叶斯定理,相信对高中数学还有印象的朋友对这个公式应该不陌生:
2.朴素贝叶斯的数据挖掘原理
下面以一个简单的例子,介绍朴素贝叶斯的数据挖掘原理。虽然样本量不多,但足以说明原理和思路。
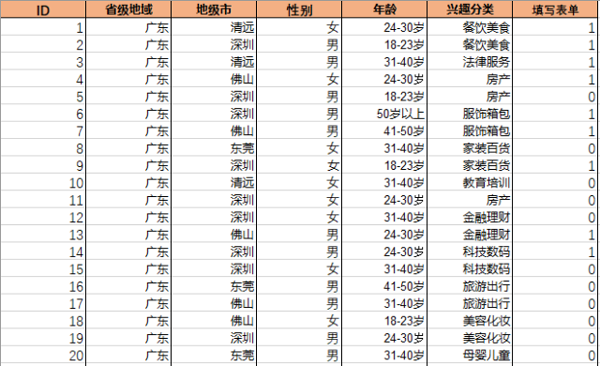
这里是一份受众画像数据,总共20笔数据,即代表20个UV。填写表单这一字段值为1的合计9笔,即发生转化的用户数为9。
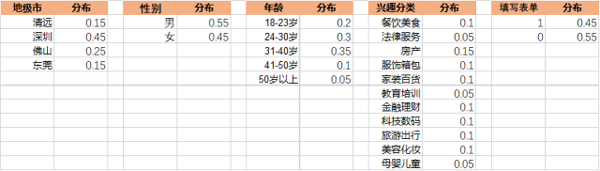
然后,我们把除了 ID(只是编号,对于挖掘没有价值)、省级地域(因为都是广东,对于挖掘没有价值)外的其他字段,做一个占比分布,如图所示:
假设,我想知道 定向 X=(地级市=”佛山”,性别=”男”,年龄=”18-23岁”,兴趣分类=”房产”)的转化率,即我想求:P(填写表单=”1″ | X)。
直接是计算不出来的,回到上文提到的朴素贝叶斯,专门解决的就是这种问题,我只需知道P(X | 填写表单=”1″),就可以通过公式得到P(填写表单=”1″ | X)。
具体的直接套公式得:
P(填写表单=”1″ | X) = P(X | 填写表单=”1″) * P(填写表单=”1″) / P(X)
同理可得,
P(填写表单=”0″ | X) = P(X | 填写表单=”0″) * P(填写表单=”0″) / P(X)
这里需要引出另外一个重要的公式,P(A,B)代表事件A与B同时发生的概率。
当事件A与B的发生是各自独立时,P(A,B) = P(A|B) * P(B) =P(A)P(B)。
因为,地级市、性别、年龄等这些字段(或定向)的发生可以理解为是各自独立的,所以P(X | 填写表单=”1″) = P(X ) * P(填写表单=”1″) ,又P(X | 填写表单=”1″)= P(地级市=”佛山”,性别=”男”,年龄=”18-23岁”,兴趣分类=”房产” | 填写表单=”1″)=P(地级市=”佛山” | 填写表单=”1″) * P(性别=”男” | 填写表单=”1″) * P(年龄=”18-23岁” | 填写表单=”1″) * P(兴趣分类=”房产” | 填写表单=”1″),此时,看起来同样无法直接得到的P(X | 填写表单=”1″),被拆分为看起来更简单的5个事件的概率的乘积。
带入具体值,计算得:
- P(填写表单=”1″ | X) = P(X | 填写表单=”1″) * P(填写表单=”1″) / P(X)= (3/9 * 6/9 * 2/9 * 1/9)*0.45 / P(X) = 0.002469 / P(X)……………………………………………①
- P(填写表单=”0″ | X) = P(X | 填写表单=”0″) * P(填写表单=”0″) / P(X)= (2/11 * 5/11 * 2/11 * 2/11)*0.55 / P(X) = 0.0015026 / P(X)……………………………………………②
- 接下来,遇到一个问题,P(X)是多少,不知道!不过不要紧,当定向 X的用户进来时,ta要么转化,要么不转化,所以
- P(填写表单=”1″ | X) + P(填写表单=”0″ | X) =1……………………………………………③
联立①②③,最终求出:
- P(填写表单=”1″ | X) = 62.2%
- P(填写表单=”0″ | X) = 37.8%
所以,当定向为X时,朴素贝叶斯数据挖掘模型认为,该类用户的转化率在62.2%。
3.朴素贝叶斯的数据挖掘的优势
主流的数据挖掘算法,如神经网络、决策树等。多半依赖如表1所示的数据,每一个字段代表用户的不同维度,每一行代表一个独立用户的数据。但实际优化过程中,媒体方不可能提供如此详尽的受众画像数据, 但朴素贝叶斯不一样,对原始数据的要求略低,只需提供不同维度组合下的比例,而不必细化到每一个用户的情况。
4.朴素贝叶斯的数据挖掘案例解读
4.1 原生数据及预处理
我们从今日头条广告后台拿到的数据经过简单处理后,是下面这样的:
合计13339点击,转化量为37。
4.2 计算字段重要性,确定输入字段
因为所有字段都是类别型字段(区别于数值型字段),这里介绍一个比较通用的算法,用于评估所有可能的输入字段对输出字段的重要性。
公式解读如下:
注:ABS函数,用于求绝对值。
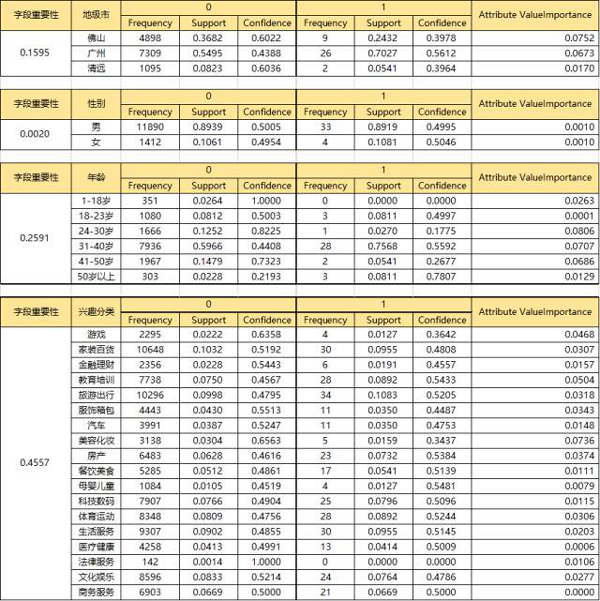
所有可能的输入字段对输出字段的重要性计算结果如下:
一般经验来说,字段重要性小于0.1的字段可以不予纳入数据挖掘模型中。
所以,目前根据有限的数据,”性别“这一字段,对于判断用户是否转化的帮助不大,故在接下来的数据挖掘模型中,输入字段包括:地级市、年龄、兴趣分类。
开始做数据挖掘,具体原理这里不再赘述,直接给出结果。
。。。(中间太长,省略了)
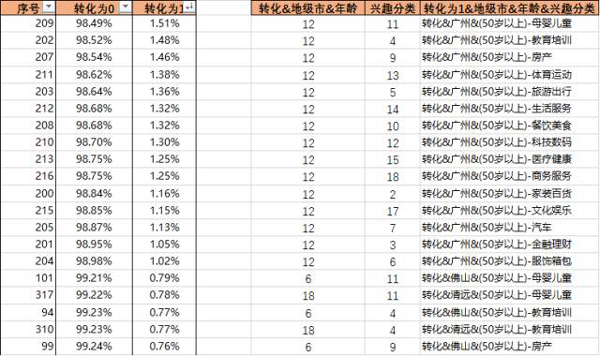
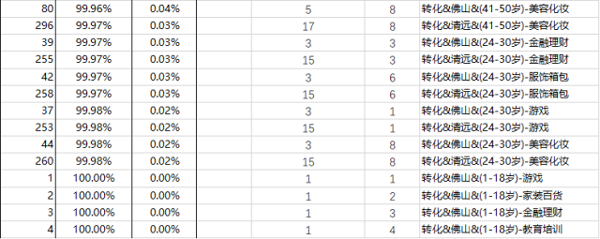
我们看到,数据挖掘显示,转化为1的最大概率是1.51%,此时的定向条件是”广州&(50岁以上)-母婴儿童“。而样本数据的整体转化率是37/13339 = 0.28%。
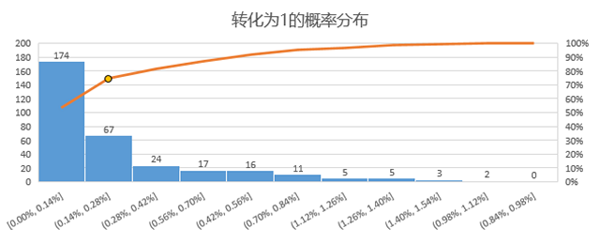
下图是转化为1的概率分布,可以看到大于0.28%的数据约有25%,换句话说,基于朴素贝叶斯的用户数据挖掘,在324种定向组合中,找到了约四分之一的组合,可以使预估的转化率高于平均水平0.28%。随着数据量的增加,模型也会不断改进,对精准定向组合的转化率预测效能也会越来越好,将有限的广告费花在最有可能转化的用户上。
下面考虑怎么将这一洞察,应用于广告投放,创造更高的ROI。比如制作针对性的创意、提高出价等等,这个方面各位都是老手了,我就不多说了。
最后强调一句,受众画像的数据挖掘需要满足一定的条件,即要能区分转化和未转化的用户。
以上,即是基于朴素贝叶斯的用户数据挖掘,给大家参考。