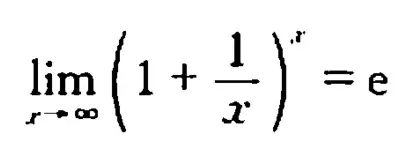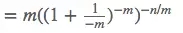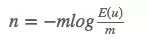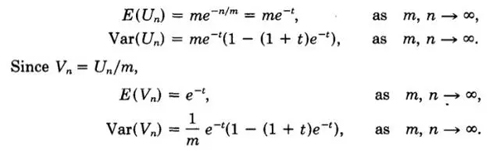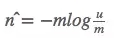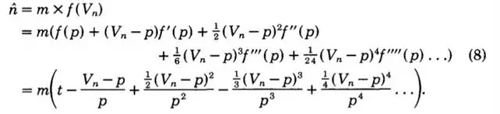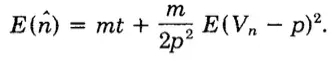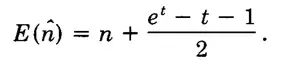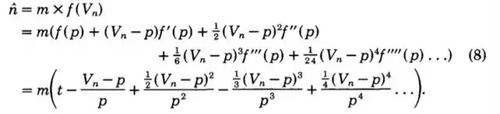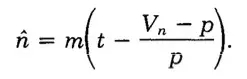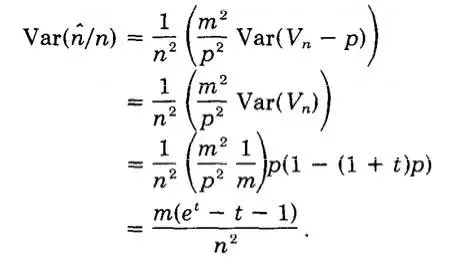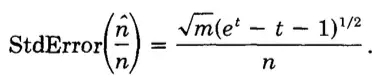今天的干货，不是一般的干，噎死人那种干。没下面这些准备的话直接退出吧，回去度娘啊谷哥啊弄懂是什么东西再回来。
知识储备必须有这些：
BitMap知识。概率论二项分布。泰勒展开。函数求极限。求期望值。求方差、标准差。log对数变换。极大似然估计。
照例甩一波链接。
来了喔。
真的来了喔。
我们先定义几个代数。
整个BitMap 有m个坑，还要有u个坑还没被占。我们已经假设了值经过 Hash 后近似服从独立均匀分布。
对事件进行定义：
A = “经过n个元素进行Hash后，第j个桶值为0”
则A出现的概率如上。意思就是坑为1的概率都是1/m，那么坑为0的概率为 (1 - 1/m)，如此重复n次 ，就得到上面的式子了。
又因为每个桶都是独立的，所以整个BitMap的期望值为A的概率直接乘以m。
做一个小小的trick(小把戏)变换，也就是强行把内部满足某个求极限的式子。喏，这个。
当m和n都趋向于无穷大的时候，求一下极限，就得到了这个
这个是有u个坑的估计，而我们想知道的是基数n，做一下log变换。
根据极大似然估计的判定定理。
既然
是可逆的，那么这样我们就得到了下面这个估计了。
好了，刚刚我们已经得到期望，现在我们求一下方差和比率t的方差和期望，后面有用，至于怎么求的，自行找一下怎么求。
我们定义一下函数f。
然后对
进行泰勒展开，得到下面这串玩意。
取前三项。原论文里说，因为第二项展开的期望为0，所以保留前三项，求期望得到
代入前面求到的期望值，化简可以得到。
所以直接除于n，可以得到偏差比率为：
至此，偏差比率的推导就完成啦，能看到这里的都是大神，说实话。
那标准差又是怎么样的呢?
还是它，泰勒展开。
这里启发性地取前两项。
一步一步推导下来，再配合前面求的方差，嗯相信你可以的。
所以标准差就是这样。
至此，原理，偏差率，标准差都推导完毕，但是还有一点点问题。就是，这样去算有什么条件呢，对于m的取值?启发性地取泰勒展开前三项和前两项又分别代表什么?这个大家自己去论文看，我要是开心，我可能也会说说看。
是不是很干货?我也知道很干，但是真的要细细阅读，读完***搭配上原始论文好好看一下，我看了蛮久的说实话。
好了睡觉了。要是觉得很干就点个赞吧，让我知道还有人在看。
【本文为51CTO专栏作者“大蕉”的原创稿件，转载请通过作者微信公众号“一名叫大蕉的程序员”获取授权】
