LTR 的入门模型就是线性模型,本文以线性模型为例,针对搜索排序的场景,通俗地介绍了机器学习的基本思想和实现步骤。作为 LTR 系列的第三篇,相信通过本文你已经可以轻松地入门 LTR。
很多搜索达人都有这样一种冲动,想要“通过机器学习获得最优权重”然后用于搜索查询中。对于搜索这件事儿来说有点像打地鼠游戏,正如通常人们所说的“如果我能选择优化‘标题匹配’的权重还是‘内容匹配’的权重,那我肯定会做得更好”!
这种学习何种权重应用于查询的本能,就是最简化机器学习排序(learning to rank,LTR)模型的根本原理:线性模型。没错,就是传说中的线性回归!线性回归非常简单易用,甚至感觉一点儿都不像是机器学习;更像是高中生的统计学一样,理解该模型及其原理也非常地容易。
本系列文章中,我想先介绍成功实施 LTR 背后的关键算法,从线性回归开始,逐步到梯度 boosting(不同种类的 boosting 算法一起)、RankSVM 和随机森林等算法。
LTR 首先是一个回归问题
对于本系列的文章,正如你在前一篇及文档中了解到的,我想把 LTR 映射为一个更加通用的问题:回归。回归问题需要训练一个模型,从而把一组数值特征映射到一个预测数值。
举个例子:你需要什么样的数据才能预测一家公司的利润?可能会有,手边的历史公共财务数据,包括雇员数量、股票价格、收益及现金流等。假设已知某些公司的数据,你的模型经过训练后用于预测这些变量(或其子集)的函数即利润。对于一家新公司,你可以使用这个函数来预测该公司的利润。
LTR 同样是一个回归问题。你手头上有一系列评价数据,来衡量一个文档与某个查询的相关度等级。我们的相关度等级取值从 A 到 F,更常见的情况是取值从 0(完全不相关)到 4(非常相关)。如果我们先考虑一个关键词搜索的查询,如下示例:
- grade,movie,keywordquery
- 4,Rocky,rocky
- 0,Turner and Hootch,rocky
- 3,Rocky II,rocky
- 1,Rambo,rocky
- ...
当构建一个模型来预测作为一个时间信号排序函数的等级时,LTR 就成为一个回归问题。 相关度搜索中的召回,即我们所说的信号,表示查询和文档间关系的任意度量;更通用的名称叫做特征,但我个人更建议叫长期信号。原因之一是,信号是典型的独立于查询的——即该结果是通过度量某个关键词(或查询的某个部分)与文档的相关程度;某些是度量它们的关系。因此我们可以引入其他信号,包括查询特有的或者文档特有的,比如一篇文章的发表日期,或者一些从查询抽取出的实体(如“公司名称”)。
来看看上面的电影示例。你可能怀疑有 2 个依赖查询的信号能帮助预测相关度:
一个搜索关键词在标题属性中出现过多少次一个搜索关键词在摘要属性中出现过多少次扩展上面的评价,可能会得到如下 CSV 文件所示的回归训练集,把具体的信号值映射为等级:
- grade,numTitleMatches,numOverviewMatches
- 4,1,1
- 0,0,0
- 3,0,3
- 1,0,1
你可以像线性回归一样应用回归流程,从而通过其他列来预测第一列。也可以在已有的搜索引擎像 Solr 或 Elasticsearch 之上来构建这样一个系统。
我回避了一个复杂问题,那就是:如何获得这些评价?如何知道一个文档对一个查询来说是好还是坏?理解用户分析?专家人工分析?这通常是最难解决的——而且是跟特定领域非常相关的!提出假设数据来建立模型虽然挺好的,但纯属做无用功!
线性回归 LTR
如果你学过一些统计学,可能已经很熟悉线性回归了。线性回归把回归问题定义为一个简单的线性函数。比如,在 LTR 中我们把上文的第一信号(一个搜索关键词在标题属性中出现过多少次)叫做 t,第二信号(一个搜索关键词在摘要属性中出现过多少次)叫做 o,我们的模型能生成一个函数 s,像下面这样对相关度来打分:
- s(t, o) = c0 + c1 * t + c2 * o
我们能评估出最佳拟合系数 c0,c1,c2 等,并使用最小二乘拟合的方法来预测我们的训练数据。这里就不赘述了,重点是我们能找到 c0,c1,c2 等来最小化实际等级 g 与预测值 s(t,o) 之间的误差。如果温习下线性代数,会发现这就像简单的矩阵数学。
使用线性回归你会更满意,包括决策确实是又一个排序信号,我们定义为 t*o。或者另一个信号 t2,实践中一般定义为 t^2 或者 log(t),或者其他你认为有利于相关度预测的最佳公式。接下来只需要把这些值作为额外的列,用于线性回归学习系数。
任何模型的设计、测试和评估是一个更深的艺术,如果希望了解更多,强烈推荐统计学习概论。
使用 sklearn 实现线性回归 LTR
为了更直观地体验,使用 Python 的 sklearn 类库来实现回归是一个便捷的方式。如果想使用上文数据通过线性回归尝试下简单的 LTR 训练集,可以把我们尝试的相关度等级预测值记为 S,我们看到的信号将预测该得分并记为 X。
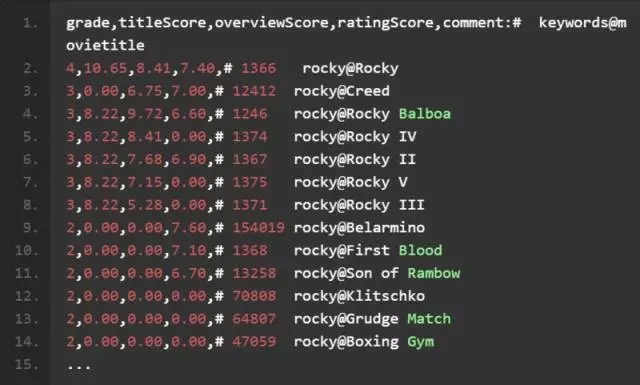
我们将使用一些电影相关度数据尝试点有趣的事情。这里有一个搜索关键词“Rocky”的相关度等级数据集。召回我们上面的评判表,转换为一个训练集。一起来体验下真实的训练集(注释会帮助我们了解具体过程)。我们将检查的三个排序信号,包括标题的 TF
IDF 得分、简介的 TF
IDF 得分以及电影观众的评分。
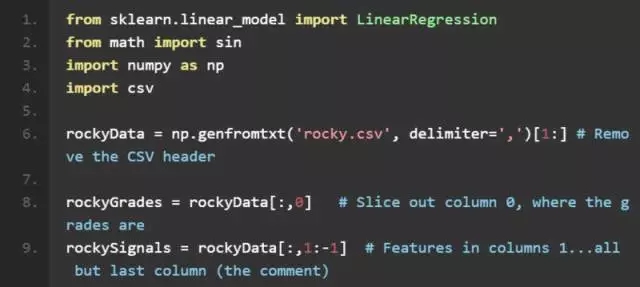
所以接下来直接来到代码的部分!下面的代码从一个 CSV 文件读取数据到一个 numpy 数组;该数组是二维的,第一维作为行,第二维作为列。在下面的注释中可以看到很新潮的数组切片是如何进行的:
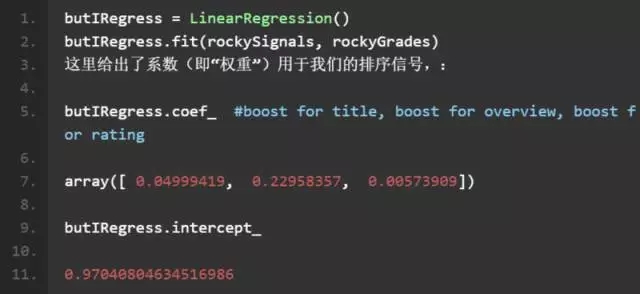
不错!我们已准备好进行一个简单线性回归了。这里我们使用一个经典的判断方法:方程比未知数多!因此我们需要使用常最小二乘法来估算特征 rockySignals 和等级 rockyGrades 间的关系。很简单,这就是 numpy 线性回归所做的:
漂亮!相关度解决了!(真的吗?)我们可以使用这些来建立一个排序函数。我们已经学习到了分别使用什么样的权重到标题和简介属性。
截至目前,我忽略了一部分事项,即我们需要考量如何评价模型和数据的匹配度。在本文的结尾,我们只是想看看一般情况下这些模型是如何工作。但不只是假设该模型非常适合训练集数据是个不错的想法,总是需要回退一些数据来测试的。接下来的博文会分别介绍这些话题。
使用模型对查询打分
我们通过这些系数可以建立自己的排序函数。做这些只是为了描述目的,sk-learn 的线性回归带有预测方法,能评估作为输入的模型,但是构建我们自己的更有意思:
使用该函数我们可以获得检索“Rambo”时,这两部候选电影的相关度得分:
现在对 Rambo 和 First Blood 打分,看看下哪一个跟查询“Rambo”更相关!
结果得分分别是 Rambo 3.670 以及 First Blood 3.671。
非常接近!First Blood 稍微高于 Rambo 一点儿获胜。原因是这样——Rambo 是一个精确匹配,而 First Blood 是 Rambo 电影前传!因此我们不应该真的让模型如此可信,并没有那么多的例子达到那个水平。更有趣的是简介得分的系数比标题得分的系数大。所以至少在这个例子中我们的模型显示,简介中提到的关键字越多,最终的相关度往往越高。至此我们已经学习到一个不错的处理策略,用来解决用户眼里的相关度!
把这个模型加进来会更有意思,这很好理解,并且产生了很合理的结果;但是特征的直接线性组合通常会因为相关度应用而达不到预期。由于缺乏这样的理由,正如 Flax 的同行所言,直接加权 boosting 也达不到预期。
为什么?细节决定成败!
从前述例子中可以发现,一些非常相关的电影确实有很高的 TF*IDF 相关度得分,但是模型却倾向于概要字段与相关度更加密切。实际上何时标题匹配以及何时概要匹配还依赖于其他因素。
在很多问题中,相关度等级与标题和摘要属性的得分并不是一个简单的线性关系,而是与上下文有关。如果就想直接搜索一个标题,那么标题肯定会更加匹配;但是对于并不太确定想要搜索标题,还是类别,或者电影的演员,甚至其他属性的情形,就不太好办了。
换句话说,相关度问题看起来并非是一个纯粹的最优化问题:
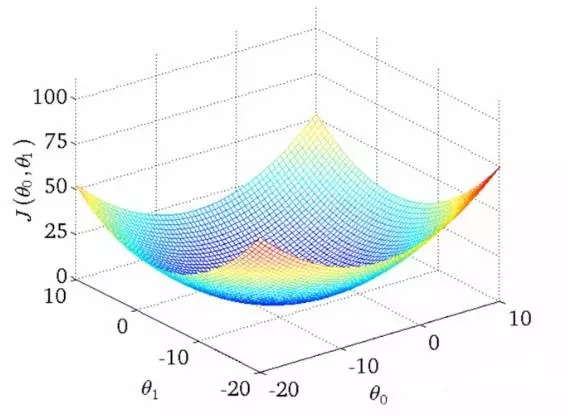
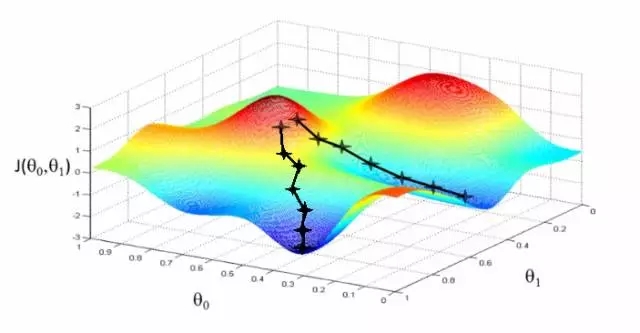
实践中的相关度要更加复杂。并没有一个神奇的最优解,宁可说很多局部最优依赖于很多其他因子的! 为什么呢?换句话说,相关度看起来如图所示:
可以想象这些图(吴恩达机器学习课程中的干货)用于展示“相关度错误” —— 离我们正在学习的分数还有多远。两个θ变量的映射表示标题和摘要的相关度得分。第一张图中有一个单一的最优值,该处的“相关度错误”最小 —— 一个理想的权重设置应用这两个查询。第二个更加实际一些:波浪起伏、上下文相关的局部最小。有时与一个非常高的标题权重值有关,或者是一个非常低的标题权重!
与上下文和细微差别密切相关!
本文到此为止。后续文章将会更多关注如何精确量化模型的适用程度。使用什么样的度量方式来评价一个模型的好坏? 这将是很重要的一步,旨在检验其他方法在捕捉细微差别方面能否做得更好。