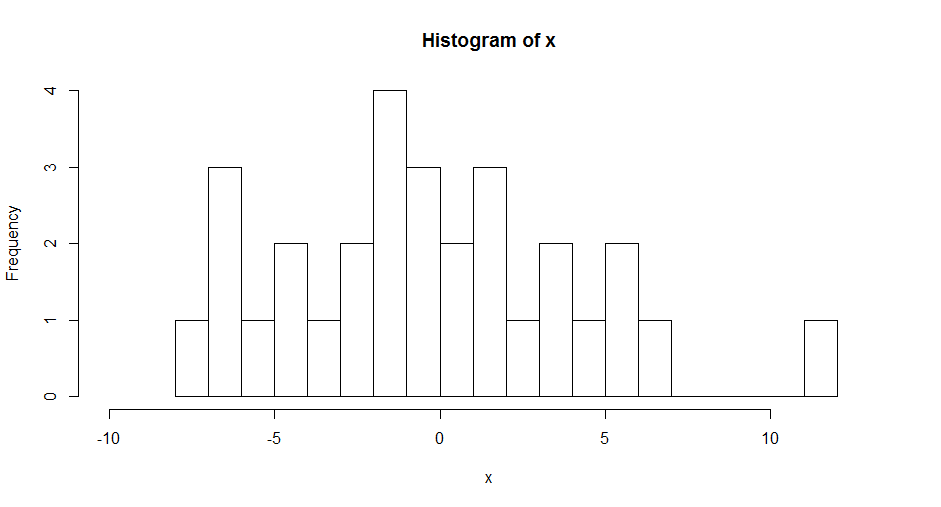民生银行高级数据分析师张丹：用R语言把数据玩出花样

【51CTO.com原创稿件】作为数据分析师，每天都有大量的数据需要处理，我们会根据业务的要求做各种复杂的报表，包括了分组、排序、过滤、转置、差分、填充、移动、合并、分裂、分布、去重、找重、填充 等等的操作。

有时为了计算一个业务指标，你的SQL怎么写都不会少于10行时，另外你可能也会抱怨Excel功能不够强大，这个时候R语言绝对是不二的选择了。用R语言可以高效地、优雅地解决数据处理的问题，让R来帮你打开面向数据的思维模式。

目录 为什么要用R语言做数据处理？ 数据处理基础 个性化的数据变换需求

1. 为什么要用R语言做数据处理？

R语言是非常适合做数据处理的编程语言，因为R语言的设计理念，就是面向数据的，为了解决数据问题。读完本文，相信你就能明白，什么是面向数据的设计了。

一个BI工程师每天的任务，都是非常繁琐的数据处理，如果用Java来做简直就是折磨，但是换成R语言来做，你会找到乐趣的。

当接到一个数据处理的任务后，我们可以把任务拆解为很多小的操作，包括了分组、排序、过滤、转置、差分、填充、移动、合并、分裂、分布、去重、找重等等的操作。对于实际应用的复杂的操作来说，就是把这些小的零碎的操作，拼装起来就好了。

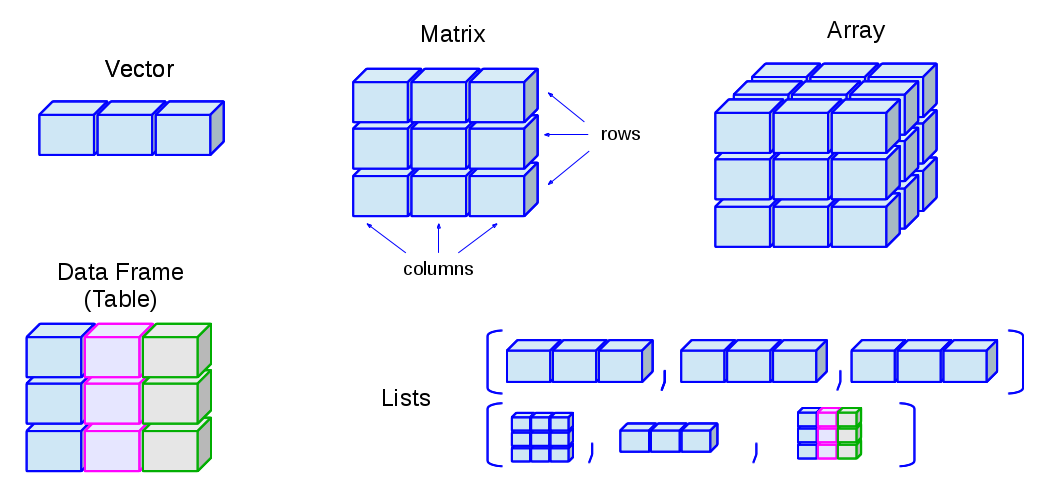
在开始之前，我们要先了解一下R语言支持的数据类型，以及这些常用类型的特点。对于BI的数据处理的工作来说，可能有4种类型是最常用的，分别是向量、矩阵、数据框、时间序列。

• 向量 Vector : c()
• 矩阵 Matrix: matrix()
• 数据框 DataFrame: data.frame()
• 时间序列 XTS: xts()

我主要是用R语言来做量化投资，很多的时候，都是和时间序列类型数据打交道，所以我把时间序列，也定义为R语言最常用的数据处理的类型。时间序列类型，使用的是第三方包xts中定义的类型。

2. 数据处理基础

本机的系统环境：

• Win10 64bit
• R: version 3.2.3 64bit

2.1 创建一个数据集

创建一个向量数据集。

> x<-1:20;x 
 [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 

创建一个矩阵数据集。

> m<-matrix(1:40,ncol=5);m 
     [,1] [,2] [,3] [,4] [,5] 
[1,]    1    9   17   25   33 
[2,]    2   10   18   26   34 
[3,]    3   11   19   27   35 
[4,]    4   12   20   28   36 
[5,]    5   13   21   29   37 
[6,]    6   14   22   30   38 
[7,]    7   15   23   31   39 
[8,]    8   16   24   32   40 

创建一个数据框数据集。

> df<-data.frame(a=1:5,b=c('A','A','B','B','A'),c=rnorm(5));df 
  a b          c 
1 1 A  1.1519118 
2 2 A  0.9921604 
3 3 B -0.4295131 
4 4 B  1.2383041 
5 5 A -0.2793463 

创建一个时间序列数据集，时间序列使用的第三方的xts类型。关于xts类型的详细介绍，请参考文章 可扩展的时间序列xts。

> library(xts) 
> xts(1:10,order.by=as.Date('2017-01-01')+1:10) 
           [,1] 
2017-01-02    1 
2017-01-03    2 
2017-01-04    3 
2017-01-05    4 
2017-01-06    5 
2017-01-07    6 
2017-01-08    7 
2017-01-09    8 
2017-01-10    9 
2017-01-11   10 

2.2 查看数据概况

通常进行数据分析的***步是，查看一下数据的概况信息，在R语言里可以使用summary()函数来完成。

# 查看矩阵数据集的概况 
> m<-matrix(1:40,ncol=5) 
> summary(m) 
       V1             V2              V3              V4              V5        
 Min.   :1.00   Min.   : 9.00   Min.   :17.00   Min.   :25.00   Min.   :33.00   
 1st Qu.:2.75   1st Qu.:10.75   1st Qu.:18.75   1st Qu.:26.75   1st Qu.:34.75   
 Median :4.50   Median :12.50   Median :20.50   Median :28.50   Median :36.50   
 Mean   :4.50   Mean   :12.50   Mean   :20.50   Mean   :28.50   Mean   :36.50   
 3rd Qu.:6.25   3rd Qu.:14.25   3rd Qu.:22.25   3rd Qu.:30.25   3rd Qu.:38.25   
 Max.   :8.00   Max.   :16.00   Max.   :24.00   Max.   :32.00   Max.   :40.00   
 
# 查看数据框数据集的概况信息 
> df<-data.frame(a=1:5,b=c('A','A','B','B','A'),c=rnorm(5)) 
> summary(df) 
       a     b           c           
 Min.   :1   A:3   Min.   :-1.5638   
 1st Qu.:2   B:2   1st Qu.:-1.0656   
 Median :3         Median :-0.2273   
 Mean   :3         Mean   :-0.1736   
 3rd Qu.:4         3rd Qu.: 0.8320   
 Max.   :5         Max.   : 1.1565   

通过查看概况，可以帮助我们简单了解数据的一些统计特征。

2.3 数据合并

我们经常需要对于数据集，进行合并操作，让数据集满足处理的需求。对于不同类型的数据集，有不同的处理方法。

向量类型

> x<-1:5 
> y<-11:15 
> c(x,y) 
 [1]  1  2  3  4  5 11 12 13 14 15 

数据框类型的合并操作。

> df<-data.frame(a=1:5,b=c('A','A','B','B','A'),c=rnorm(5));df 
  a b          c 
1 1 A  1.1519118 
2 2 A  0.9921604 
3 3 B -0.4295131 
4 4 B  1.2383041 
5 5 A -0.2793463 
 
# 合并新行 
> rbind(df,c(11,'A',222)) 
   a b                  c 
1  1 A    1.1519117540872 
2  2 A  0.992160365445798 
3  3 B -0.429513109491881 
4  4 B   1.23830410085338 
5  5 A -0.279346281854269 
6 11 A                222 
 
# 合并新列 
> cbind(df,x=LETTERS[1:5]) 
  a b          c x 
1 1 A  1.1519118 A 
2 2 A  0.9921604 B 
3 3 B -0.4295131 C 
4 4 B  1.2383041 D 
5 5 A -0.2793463 E 
 
# 合并新列 
> merge(df,LETTERS[3:5]) 
   a b          c y 
1  1 A  1.1519118 C 
2  2 A  0.9921604 C 
3  3 B -0.4295131 C 
4  4 B  1.2383041 C 
5  5 A -0.2793463 C 
6  1 A  1.1519118 D 
7  2 A  0.9921604 D 
8  3 B -0.4295131 D 
9  4 B  1.2383041 D 
10 5 A -0.2793463 D 
11 1 A  1.1519118 E 
12 2 A  0.9921604 E 
13 3 B -0.4295131 E 
14 4 B  1.2383041 E 
15 5 A -0.2793463 E 

2.4 累计计算

累计计算，是很常用的一种计算方法，就是把每个数值型的数据，累计求和或累计求积，从而反应数据的增长的一种特征。

# 向量x 
> x<-1:10;x 
 [1]  1  2  3  4  5  6  7  8  9 10 
 
# 累计求和 
> cum_sum<-cumsum(x) 
 
# 累计求积 
> cum_prod<-cumprod(x) 
 
# 拼接成data.frame 
> data.frame(x,cum_sum,cum_prod) 
    x cum_sum cum_prod 
1   1       1        1 
2   2       3        2 
3   3       6        6 
4   4      10       24 
5   5      15      120 
6   6      21      720 
7   7      28     5040 
8   8      36    40320 
9   9      45   362880 
10 10      55  3628800 

我们通常用累计计算，记录中间每一步的过程，看到的数据处理过程的特征。

2.5 差分计算

差分计算，是用向量的后一项减去前一项，所获得的差值，差分的结果反映了离散量之间的一种变化。

> x<-1:10;x 
 [1]  1  2  3  4  5  6  7  8  9 10 
 
# 计算1阶差分 
> diff(x) 
[1] 1 1 1 1 1 1 1 1 1 
 
# 计算2阶差分 
> diff(x,2) 
[1] 2 2 2 2 2 2 2 2 
 
# 计算2阶差分，迭代2次 
> diff(x,2,2) 
[1] 0 0 0 0 0 0 

下面做一个稍微复杂一点的例子，通过差分来发现数据的规律。

# 对向量2次累积求和 
> x <- cumsum(cumsum(1:10));x 
 [1]   1   4  10  20  35  56  84 120 165 220 
 
# 计算2阶差分 
> diff(x, lag = 2) 
[1]   9  16  25  36  49  64  81 100 
 
# 计算1阶差分，迭代2次 
> diff(x, differences = 2) 
[1]  3  4  5  6  7  8  9 10 
 
# 同上 
> diff(diff(x)) 
[1]  3  4  5  6  7  8  9 10 

差分其实是很常见数据的操作，但这种操作是SQL很难表达的，所以可能会被大家所忽视。

2.6 分组计算

分组是SQL中，支持的一种数据变换的操作，对应于group by的语法。

比如，我们写一个例子。创建一个数据框有a,b,c的3列，其中a,c列为数值型，b列为字符串，我们以b列分组，求出a列与c的均值。

# 创建数据框 
> df<-data.frame(a=1:5,b=c('A','A','B','B','A'),c=rnorm(5));df 
  a b           c 
1 1 A  1.28505418 
2 2 A -0.04687263 
3 3 B  0.25383533 
4 4 B  0.70145787 
5 5 A -0.11470372 
 
# 执行分组操作 
> aggregate(. ~ b, data = df, mean) 
  b        a         c 
1 A 2.666667 0.3744926 
2 B 3.500000 0.4776466 

同样的数据集，以b列分组，对a列求和，对c列求均值。当对不同列，进行不同的操作时，我们同时也需要换其他函数来处理。

# 加载plyr库 
> library(plyr) 
 
# 执行分组操作 
> ddply(df,.(b),summarise, 
+       sum_a=sum(a), 
+       mean_c=mean(c)) 
  b sum_a      mean_c 
1 A     8 -0.05514761 
2 B     7  0.82301276 

生成的结果，就是按b列进行分组后，a列求和，c列求均值。

2.7 分裂计算

分裂计算，是把一个向量按照一列规则，拆分成多个向量的操作。

如果你想把1:10的向量，按照单双数，拆分成2个向量。

> split(1:10, 1:2) 
$`1` 
[1] 1 3 5 7 9 
 
$`2` 
[1]  2  4  6  8 10 

另外，可以用因子类型来控制分裂。分成2步操作，***步先分成与数据集同样长度的因子，第二步进行分裂，可以把一个大的向量拆分成多个小的向量。

# 生成因子规则 
> n <- 3; size <- 5 
> fat <- factor(round(n * runif(n * size)));fat 
 [1] 2 3 2 1 1 0 0 2 0 1 2 3 1 1 1 
Levels: 0 1 2 3 
 
# 生成数据向量 
> x <- rnorm(n * size);x 
 [1]  0.68973936  0.02800216 -0.74327321  0.18879230 -1.80495863  1.46555486  0.15325334  2.17261167  0.47550953 
[10] -0.70994643  0.61072635 -0.93409763 -1.25363340  0.29144624 -0.44329187 
 
# 对向量以因子的规则进行拆分 
> split(x, fat) 
$`0` 
[1] 1.4655549 0.1532533 0.4755095 
 
$`1` 
[1]  0.1887923 -1.8049586 -0.7099464 -1.2536334  0.2914462 -0.4432919 
 
$`2` 
[1]  0.6897394 -0.7432732  2.1726117  0.6107264 
 
$`3` 
[1]  0.02800216 -0.93409763 

这种操作可以非常有效地，对数据集进行分类整理，比if..else的操作，有本质上的提升。

2.8 排序

排序是所有数据操作中，最常见一种需求了。在R语言中，你可以很方便的使用排序的功能，并不用考虑时间复杂度与空间复杂度的问题，除非你自己非要用for循环来实现。

对向量进行排序。

# 生成一个乱序的向量 
> x<-sample(1:10);x 
 [1]  6  2  5  1  9 10  8  3  7  4 
 
# 对向量排序  
> x[order(x)] 
 [1]  1  2  3  4  5  6  7  8  9 10 

以数据框某一列进行排序。

> df<-data.frame(a=1:5,b=c('A','A','B','B','A'),c=rnorm(5));df 
  a b          c 
1 1 A  1.1780870 
2 2 A -1.5235668 
3 3 B  0.5939462 
4 4 B  0.3329504 
5 5 A  1.0630998 
 
# 自定义排序函数  
> order_df<-function(df,col,decreasing=FALSE){ 
+     df[order(df[,c(col)],decreasing=decreasing),] 
+ } 
 
# 以c列倒序排序 
> order_df(df,'c',decreasing=TRUE) 
  a b          c 
1 1 A  1.1780870 
5 5 A  1.0630998 
3 3 B  0.5939462 
4 4 B  0.3329504 
2 2 A -1.5235668 

排序的操作，大多都是基于索引来完成的，用order()函数来生成索引，再匹配的数据的数值上面。

2.9 去重与找重

去重，是把向量中重复的元素过滤掉。找重，是把向量中重复的元素找出来。

> x<-c(3:6,5:8);x 
[1] 3 4 5 6 5 6 7 8 
 
# 去掉重复元素 
> unique(x) 
[1] 3 4 5 6 7 8 
 
# 找到重复元素，索引位置 
> duplicated(x) 
[1] FALSE FALSE FALSE FALSE  TRUE  TRUE FALSE FALSE 
 
# 找到重复元素 
> x[duplicated(x)] 
[1] 5 6 

2.10 转置

转置是一个数学名词，把行和列进行互换，一般用于对矩阵的操作。

# 创建一个3行5列的矩阵 
> m<-matrix(1:15,ncol=5);m 
     [,1] [,2] [,3] [,4] [,5] 
[1,]    1    4    7   10   13 
[2,]    2    5    8   11   14 
[3,]    3    6    9   12   15 
 
# 转置后，变成5行3列的矩阵 
> t(m) 
     [,1] [,2] [,3] 
[1,]    1    2    3 
[2,]    4    5    6 
[3,]    7    8    9 
[4,]   10   11   12 
[5,]   13   14   15 

2.11 过滤

过滤，是对数据集按照某种规则进行筛选，去掉不符合条件的数据，保留符合条件的数据。对于NA值的操作，主要都集中在了过滤操作和填充操作中，因此就不在单独介绍NA值的处理了。

# 生成数据框 
> df<-data.frame(a=c(1,NA,NA,2,NA), 
+     b=c('B','A','B','B',NA), 
+     c=c(rnorm(2),NA,NA,NA));df 
   a    b          c 
1  1    B -0.3041839 
2 NA    A  0.3700188 
3 NA    B         NA 
4  2    B         NA 
5 NA <NA>         NA 
 
# 过滤有NA行的数据 
> na.omit(df) 
  a b          c 
1 1 B -0.3041839 
 
# 过滤，保留b列值为B的数据 
> df[which(df$b=='B'),] 
   a b          c 
1  1 B -0.3041839 
3 NA B         NA 
4  2 B         NA 

过滤，类似与SQL语句中的 WHERE 条件语句，如果你用100个以上的过滤条件，那么你的程序就会比较复杂了，***想办法用一些巧妙的函数或者设计模式，来替换这些过滤条件。

2.12 填充

填充，是一个比较有意思的操作，你的原始数据有可能会有缺失值NA，在做各种计算时，就会出现有问题。一种方法是，你把NA值都去掉；另外一种方法是，你把NA值进行填充后再计算。那么在填充值时，就有一些讲究了。

把NA值进行填充。

# 生成数据框 
> df<-data.frame(a=c(1,NA,NA,2,NA), 
+      b=c('B','A','B','B',NA), 
+      c=c(rnorm(2),NA,NA,NA));df 
   a    b          c 
1  1    B  0.2670988 
2 NA    A -0.5425200 
3 NA    B         NA 
4  2    B         NA 
5 NA <NA>         NA 
 
# 把数据框a列的NA，用9进行填充 
> na.fill(df$a,9) 
[1] 1 9 9 2 9 
 
# 把数据框中的NA，用1进行填充 
> na.fill(df,1) 
     a      b      c            
[1,] " 1"   "B"    " 0.2670988" 
[2,] "TRUE" "A"    "-0.5425200" 
[3,] "TRUE" "B"    "TRUE"       
[4,] " 2"   "B"    "TRUE"       
[5,] "TRUE" "TRUE" "TRUE"      

填充时，有时并不是用某个固定的值，而是需要基于某种规则去填充。

# 生成一个zoo类型的数据 
> z <- zoo(c(2, NA, 1, 4, 5, 2), c(1, 3, 4, 6, 7, 8));z 
 1  3  4  6  7  8  
 2 NA  1  4  5  2  
 
# 对NA进行线性插值 
> na.approx(z)  
       1        3        4        6        7        8  
2.000000 1.333333 1.000000 4.000000 5.000000 2.000000  
 
# 对NA进行线性插值 
> na.approx(z, 1:6) 
  1   3   4   6   7   8  
2.0 1.5 1.0 4.0 5.0 2.0  
 
# 对NA进行样条插值 
> na.spline(z) 
        1         3         4         6         7         8  
2.0000000 0.1535948 1.0000000 4.0000000 5.0000000 2.0000000  

另外，我们可以针对NA的位置进行填充，比如用前值来填充或后值来填充。

> df 
   a    b          c 
1  1    B  0.2670988 
2 NA    A -0.5425200 
3 NA    B         NA 
4  2    B         NA 
5 NA <NA>         NA 
 
# 用当前列中，NA的前值来填充 
> na.locf(df) 
   a b          c 
1  1 B  0.2670988 
2  1 A -0.5425200 
3  1 B -0.5425200 
4  2 B -0.5425200 
5  2 B -0.5425200 
 
# 用当前列中，NA的后值来填充 
> na.locf(df,fromLast=TRUE) 
   a b          c 
1  1 B  0.2670988 
2  2 A -0.5425200 
3  2 B       <NA> 
4  2 B       <NA> 

2.13 计数

计数，是统计同一个值出现的次数。

# 生成30个随机数的向量 
> set.seed(0) 
> x<-round(rnorm(30)*5);x 
 [1]  6 -2  7  6  2 -8 -5 -1  0 12  4 -4 -6 -1 -1 -2  1 -4  2 -6 -1  2  1  4  0  3  5 -3 -6  0 
 
# 统计每个值出现的次数 
> table(x) 
x 
-8 -6 -5 -4 -3 -2 -1  0  1  2  3  4  5  6  7 12  
 1  3  1  2  1  2  4  3  2  3  1  2  1  2  1  1  

用直方图画出。

> hist(x,xlim = c(-10,13),breaks=20) 

2.14 统计分布

统计分布，是用来判断数据是否是满足某种统计学分布，如果能够验证了，那么我们就可以用到这种分布的特性来理解我们的数据集的情况了。常见的连续型的统计分布有9种，其中最常用的就是正态分布的假设。关于统计分布的详细介绍，请参考文章 常用连续型分布介绍及R语言实现。

• runif() :均匀分布
• rnorm() :正态分布
• rexp() :指数分布
• rgamma() :伽马分布
• rweibull() :韦伯分布
• rchisq() :卡方分布
• rf() :F分布
• rt() :T分布
• rbeta() :贝塔分布

统计模型定义的回归模型，就是基于正态分布的做的数据假设，如果残差满足正态分布，模型的指标再漂亮都是假的。如果你想进一步了解回归模型，请参考文章R语言解读一元线性回归模型。

下面用正态分布，来举例说明一下。假设我们有一组数据，是人的身高信息，我们知道平均身高是170cm，然后我们算一下，这组身高数据是否满足正态分布。

# 生成身高数据 
> set.seed(1) 
> x<-round(rnorm(100,170,10)) 
> head(x,20) 
 [1] 164 172 162 186 173 162 175 177 176 167 185 174 164 148 181 170 170 179 178 176 
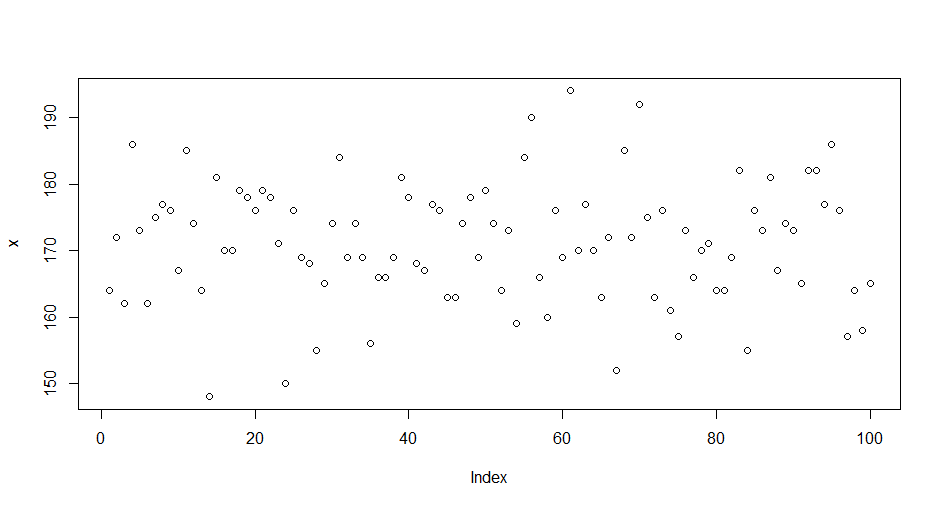
# 画出散点图  
> plot(x) 

通过散点图来观察，发现数据是没有任何规律。接下来，我们进行正态分布的检验，Shapiro-Wilk进行正态分布检验。

> shapiro.test(x) 
    Shapiro-Wilk normality test 
data:  x 
W = 0.99409, p-value = 0.9444 

该检验原假设为H0:数据集符合正态分布，统计量W为0.99409。统计量W的***值是1，越接近1，表示样本与正态分布越匹配。p值，如果p-value小于显著性水平α(0.05)，则拒绝H0。检验结论: W接近1，p-value>0.05，不能拒绝原假设，所以数据集S符合正态分布！

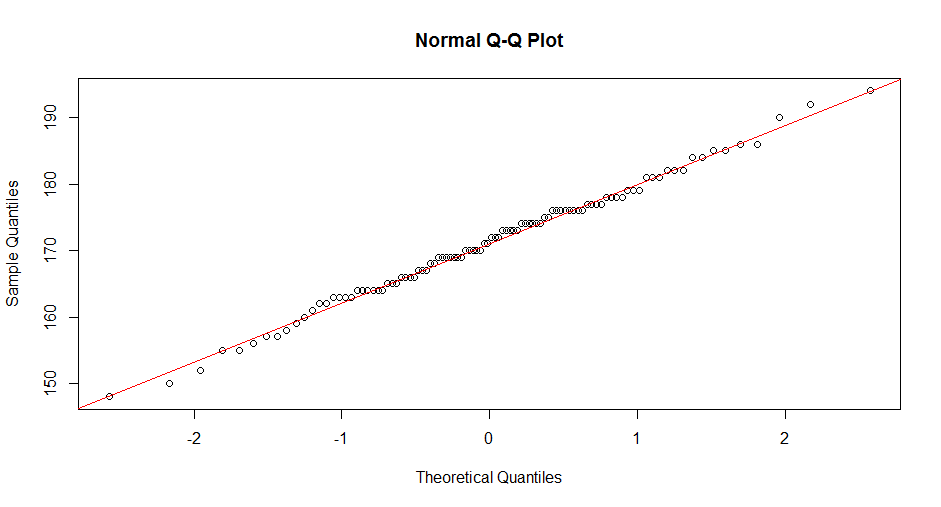
同时，我们也可以用QQ图，来做正态分布的检验。

> qqnorm(x) 
> qqline(x,col='red') 

图中，散点均匀的分布在对角线，则说明这组数据符合正态分布。

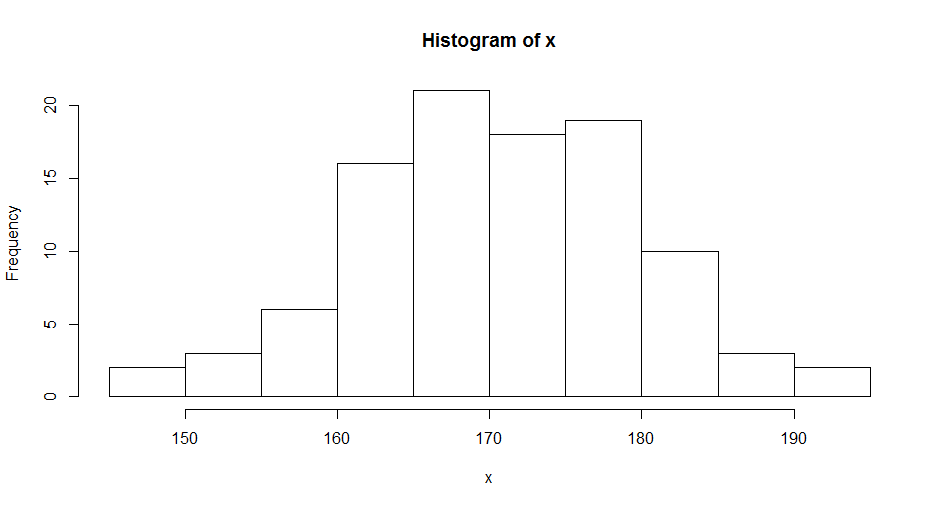
为了，更直观地对正态分布的数据进行观察，我们可以用上文中计数操作时，使用的直方图进行观察。

> hist(x,breaks=10) 

通过计数的方法，发现数据形状如钟型，中间高两边低，中间部分的数量占了95%，这就是正态的特征。当判断出，数据是符合正态分布后，那么才具备了可以使用一些的模型的基础。

2.15 数值分段

数值分段，就是把一个连续型的数值型数据，按区间分割为因子类型的离散型数据。

> x<-1:10;x 
 [1]  1  2  3  4  5  6  7  8  9 10 
 
# 把向量转换为3段因子，分别列出每个值对应因子 
> cut(x, 3) 
 [1] (0.991,4] (0.991,4] (0.991,4] (0.991,4] (4,7]     (4,7]     (4,7]     (7,10]    (7,10]    (7,10]    
Levels: (0.991,4] (4,7] (7,10] 
 
# 对因子保留2位精度，并支持排序 
> cut(x, 3, dig.lab = 2, ordered = TRUE) 
 [1] (0.99,4] (0.99,4] (0.99,4] (0.99,4] (4,7]    (4,7]    (4,7]    (7,10]   (7,10]   (7,10]   
Levels: (0.99,4] < (4,7] < (7,10] 

2.16 集合操作

集合操作，是对2个向量的操作，处理2个向量之间的数值的关系，找到包含关系、取交集、并集、差集等。

# 定义2个向量x,y 
> x<-c(3:8,NA);x 
[1]  3  4  5  6  7  8 NA 
> y<-c(NA,6:10,NA);y 
[1] NA  6  7  8  9 10 NA 
 
# 判断x与y重复的元素的位置 
> is.element(x, y) 
[1] FALSE FALSE FALSE  TRUE  TRUE  TRUE  TRUE 
 
# 判断y与x重复的元素的位置 
> is.element(y, x) 
[1]  TRUE  TRUE  TRUE  TRUE FALSE FALSE  TRUE 
 
# 取并集 
> union(x, y) 
[1]  3  4  5  6  7  8 NA  9 10 
 
# 取交集 
> intersect(x, y) 
[1]  6  7  8 NA 
 
# 取x有，y没有元素 
> setdiff(x, y) 
[1] 3 4 5 
 
# 取y有，x没有元素 
> setdiff(y, x) 
[1]  9 10 
 
# 判断2个向量是否相等 
> setequal(x, y) 
[1] FALSE 

2.17 移动窗口

移动窗口，是用来按时间周期观察数据的一种方法。移动平均，就是一种移动窗口的最常见的应用了。

在R语言的的TTR包中，支持多种的移动窗口的计算。

• runMean(x) :移动均值
• runSum(x) :移动求和
• runSD(x) :移动标准差
• runVar(x) :移动方差
• runCor(x,y) :移动相关系数
• runCov(x,y) :移动协方差
• runMax(x) :移动***值
• runMin(x) :移动最小值
• runMedian(x):移动中位数

下面我们用移动平均来举例说明一下，移动平均在股票交易使用的非常普遍，是最基础的趋势判断的根踪指标了。

# 生成50个随机数 
> set.seed(0) 
> x<-round(rnorm(50)*10);head(x,10) 
 [1]  13  -3  13  13   4 -15  -9  -3   0  24 
 
# 加载TTR包 
> library(TTR) 
 
# 计算周期为3的移动平均值 
> m3<-SMA(x,3);head(m3,10) 
 [1]         NA         NA  7.6666667  7.6666667 10.0000000  0.6666667 -6.6666667 -9.0000000 -4.0000000 
[10]  7.0000000 
 
# 计算周期为5的移动平均值 
> m5<-SMA(x,5);head(m5,10) 
 [1]   NA   NA   NA   NA  8.0  2.4  1.2 -2.0 -4.6 -0.6 

当计算周期为3的移动平均值时，结果的前2个值是NA，计算的算法是

(***个值 + 第二个值 + 第三个值)  /3 = 第三个值的移动平均值 
(13      +    -3   +     13)    /3 = 7.6666667 

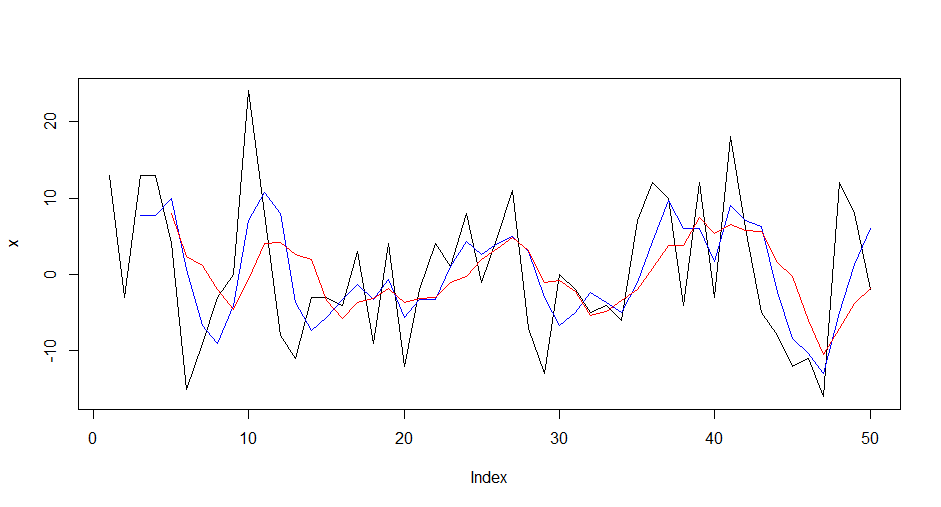
画出图形

> plot(x,type='l') 
> lines(m3,col='blue') 
> lines(m5,col='red') 

图中黑色线是原始数据，蓝色线是周期为3的移动平均值，红色线是周期为5的移动平均值。这3个线中，周期越大的越平滑，红色线波动是最小的，趋势性是越明显的。如果你想更深入的了解移动平均线在股票中的使用情况，请参考文章二条均线打天下 。

2.18 时间对齐

时间对齐，是在处理时间序列类型时常用到的操作。我们在做金融量化分析时，经常遇到时间不齐的情况，比如某支股票交易很活跃，每一秒都有交易，而其他不太活跃的股票，可能1分钟才有一笔交易，当我们要同时分析这2只股票的时候，就需要把他们的交易时间进行对齐。

# 生成数据，每秒一个值 
> a<-as.POSIXct("2017-01-01 10:00:00")+0:300 
 
# 生成数据，每59秒一个值 
> b<-as.POSIXct("2017-01-01 10:00")+seq(1,300,59) 
 
# 打印a 
> head(a,10) 
 [1] "2017-01-01 10:00:00 CST" "2017-01-01 10:00:01 CST" "2017-01-01 10:00:02 CST" "2017-01-01 10:00:03 CST" 
 [5] "2017-01-01 10:00:04 CST" "2017-01-01 10:00:05 CST" "2017-01-01 10:00:06 CST" "2017-01-01 10:00:07 CST" 
 [9] "2017-01-01 10:00:08 CST" "2017-01-01 10:00:09 CST" 
 
# 打印b  
> head(b,10) 
[1] "2017-01-01 10:00:01 CST" "2017-01-01 10:01:00 CST" "2017-01-01 10:01:59 CST" "2017-01-01 10:02:58 CST" 
[5] "2017-01-01 10:03:57 CST" "2017-01-01 10:04:56 CST" 

按分钟进行对齐，把时间都对齐到分钟线上。

# 按分钟对齐 
> a1<-align.time(a, 1*60) 
> b1<-align.time(b, 1*60) 
 
# 查看对齐后的结果 
> head(a1,10) 
 [1] "2017-01-01 10:01:00 CST" "2017-01-01 10:01:00 CST" "2017-01-01 10:01:00 CST" "2017-01-01 10:01:00 CST" 
 [5] "2017-01-01 10:01:00 CST" "2017-01-01 10:01:00 CST" "2017-01-01 10:01:00 CST" "2017-01-01 10:01:00 CST" 
 [9] "2017-01-01 10:01:00 CST" "2017-01-01 10:01:00 CST" 
 
> head(b1,10) 
[1] "2017-01-01 10:01:00 CST" "2017-01-01 10:02:00 CST" "2017-01-01 10:02:00 CST" "2017-01-01 10:03:00 CST" 
[5] "2017-01-01 10:04:00 CST" "2017-01-01 10:05:00 CST" 

由于a1数据集，每分钟有多条数据，取每分钟的***一条代表这分钟就行。

> a1[endpoints(a1,'minutes')] 
[1] "2017-01-01 10:01:00 CST" "2017-01-01 10:02:00 CST" "2017-01-01 10:03:00 CST" "2017-01-01 10:04:00 CST" 
[5] "2017-01-01 10:05:00 CST" "2017-01-01 10:06:00 CST" 

这样子就完成了时间对齐，把不同时间的数据放到都一个维度中了。

3. 个性化的数据变换需求

我们上面已经介绍了，很多种的R语言数据处理的方法，大多都是基于R语言内置的函数或第三方包来完成的。在实际的工作中，实际还有再多的操作，完全是各性化的。

3.1 过滤数据框中，列数据全部为空的列

空值，通常都会给我们做数值计算，带来很多麻烦。有时候一列的数据都是空时，我们需要先把这一个过滤掉，再进行数据处理。

用R语言程序进行实现

# 判断哪列的值都是NA 
na_col_del_df<-function(df){ 
  df[,which(!apply(df,2,function(x) all(is.na(x))))]   
}  
 
# 生成一个数据集 
> df<-data.frame(a=c(1,NA,2,4),b=rep(NA,4),c=1:4);df 
   a  b c 
1  1 NA 1 
2 NA NA 2 
3  2 NA 3 
4  4 NA 4 
 
# 保留非NA的列 
> na_col_del_df(df) 
   a c 
1  1 1 
2 NA 2 
3  2 3 
4  4 4 

3.2 替换数据框中某个区域的数据

我们想替换数据框中某个区域的数据，那么应该怎么做呢？

找到***个数据框中，与第二个数据框中匹配的行的值作为条件，然后替换这一行的其他指定列的值。

> replace_df<-function(df1,df2,keys,vals){ 
+     row1<-which(apply(mapply(match,df1[,keys],df2[,keys])>0,1,all)) 
+     row2<-which(apply(mapply(match,df2[,keys],df1[,keys])>0,1,all)) 
+     df1[row1,vals]<-df2[row2,vals] 
+     return(df1) 
+ } 
 
# ***个数据框  
> df1<-data.frame(A=c(1,2,3,4),B=c('a','b','c','d'),C=c(0,4,0,4),D=1:4);df1 
  A B C D 
1 1 a 0 1 
2 2 b 4 2 
3 3 c 0 3 
4 4 d 4 4 
 
# 第二个数据框  
> df2<-data.frame(A=c(1,3),B=c('a','c'),C=c(9,9),D=rep(8,2));df2 
  A B C D 
1 1 a 9 8 
2 3 c 9 8 
 
# 定义匹配条件列  
> keys=c("A","B") 
 
# 定义替换的列 
> vals=c("C","D") 
 
# 数据替换 
> replace_df(df1,df2,keys,vals) 
  A B C D 
1 1 a 9 8 
2 2 b 4 2 
3 3 c 9 8 
4 4 d 4 4 

其实不管R语言中，各种内置的功能函数有多少，自己做在数据处理的时候，都要自己构建很多DIY的函数。

3.3 长表和宽表变换

长宽其实是一种类对于标准表格形状的描述，长表变宽表，是把一个行数很多的表，让其行数减少，列数增加，宽表变长表，是把一个表格列数减少行数增加。

长表变宽表，指定program列不动，用fun列的每一行，生成新的列，再用time列的每个值进行填充。

# 创建数据框 
> df<-data.frame( 
+     program=rep(c('R','Java','PHP','Python'),3), 
+     fun=rep(c('fun1','fun2','fun3'),each = 4), 
+     time=round(rnorm(12,10,3),2) 
+ );df 
   program  fun  time 
1        R fun1 15.01 
2     Java fun1  7.17 
3      PHP fun1 10.84 
4   Python fun1  8.96 
5        R fun2 10.30 
6     Java fun2  9.45 
7      PHP fun2  8.87 
8   Python fun2  8.18 
9        R fun3  6.30 
10    Java fun3  9.70 
11     PHP fun3  8.89 
12  Python fun3  5.19 
 
# 加载reshape2库 
> library(reshape2) 
 
# 长表变宽表 
> wide <- reshape(df,v.names="time",idvar="program",timevar="fun",direction = "wide");wide 
  program time.fun1 time.fun2 time.fun3 
1       R      8.31      8.72     10.10 
2    Java      8.45      4.15     13.86 
3     PHP     10.49     11.47      9.96 
4  Python     10.45     13.25     14.64 

接下来，进行反正操作，把宽表再转换为长表，还是使用reshape()函数。

# 宽表变为长表 
> reshape(wide, direction = "long") 
            program  fun  time 
R.fun1            R fun1  8.31 
Java.fun1      Java fun1  8.45 
PHP.fun1        PHP fun1 10.49 
Python.fun1  Python fun1 10.45 
R.fun2            R fun2  8.72 
Java.fun2      Java fun2  4.15 
PHP.fun2        PHP fun2 11.47 
Python.fun2  Python fun2 13.25 
R.fun3            R fun3 10.10 
Java.fun3      Java fun3 13.86 
PHP.fun3        PHP fun3  9.96 
Python.fun3  Python fun3 14.64 

我们在宽表转换为长表时，可以指定想转换部分列，而不是所有列，这样就需要增加一个参数进行控制。比如，只变换time.fun2，time.fun3列到长表，而不变换time.fun1列。

> reshape(wide, direction = "long", varying =3:4) 
       program time.fun1  time id 
1.fun2       R      8.31  8.72  1 
2.fun2    Java      8.45  4.15  2 
3.fun2     PHP     10.49 11.47  3 
4.fun2  Python     10.45 13.25  4 
1.fun3       R      8.31 10.10  1 
2.fun3    Java      8.45 13.86  2 
3.fun3     PHP     10.49  9.96  3 
4.fun3  Python     10.45 14.64  4 

这样子的转换变形，是非常有利于我们从多角度来看数据的。

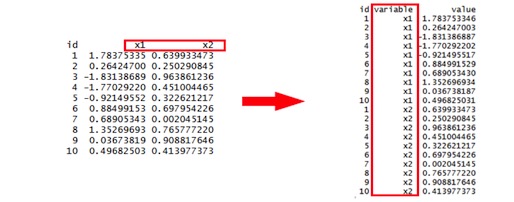
3.4 融化

融化，用于把以列进行分组的数据，转型为按行存储，对应数据表设计的概念为，属性表设计。

 

我们设计一下标准的二维表结构，然后按属性表的方式进行转换。

# 构建数据集 
> df<-data.frame( 
+   id=1:10, 
+   x1=rnorm(10), 
+   x2=runif(10,0,1) 
+ );df 
   id          x1          x2 
1   1  1.78375335 0.639933473 
2   2  0.26424700 0.250290845 
3   3 -1.83138689 0.963861236 
4   4 -1.77029220 0.451004465 
5   5 -0.92149552 0.322621217 
6   6  0.88499153 0.697954226 
7   7  0.68905343 0.002045145 
8   8  1.35269693 0.765777220 
9   9  0.03673819 0.908817646 
10 10  0.49682503 0.413977373 
 
# 融合，以id列为固定列 
> melt(df, id="id") 
   id variable        value 
1   1       x1  1.783753346 
2   2       x1  0.264247003 
3   3       x1 -1.831386887 
4   4       x1 -1.770292202 
5   5       x1 -0.921495517 
6   6       x1  0.884991529 
7   7       x1  0.689053430 
8   8       x1  1.352696934 
9   9       x1  0.036738187 
10 10       x1  0.496825031 
11  1       x2  0.639933473 
12  2       x2  0.250290845 
13  3       x2  0.963861236 
14  4       x2  0.451004465 
15  5       x2  0.322621217 
16  6       x2  0.697954226 
17  7       x2  0.002045145 
18  8       x2  0.765777220 
19  9       x2  0.908817646 
20 10       x2  0.413977373 

这个操作其实在使用ggplot2包画图时，会被经常用到。因为ggplot2做可视化时画多条曲线时，要求的输入的数据格式必须时属性表的格式。

3.5 周期分割

周期分割，是基于时间序列类型数据的处理。比如黄金的交易，你可以用1天为周期来观察，也可以用的1小时为周期来观察，也可以用1分钟为周期来看。

下面我们尝试先生成交易数据，再对交易数据进行周期的分割。本例仅为周期分割操作的示范，数据为随机生成的，请不要对数据的真实性较真。

# 加载xts包 
> library(xts) 
 
# 定义生成每日交易数据函数 
> newTick<-function(date='2017-01-01',n=30){ 
+   newDate<-paste(date,'10:00:00') 
+   xts(round(rnorm(n,10,2),2),order.by=as.POSIXct(newDate)+seq(0,(n-1)*60,60)) 
+ } 

假设我们要生成1年的交易数据，先产生1年的日期向量，然后循环生成每日的数据。

# 设置交易日期 
> dates<-as.Date("2017-01-01")+seq(0,360,1) 
> head(dates) 
[1] "2017-01-01" "2017-01-02" "2017-01-03" "2017-01-04" "2017-01-05" "2017-01-06" 
 
# 生成交易数据 
> xs<-lapply(dates,function(date){ 
+   newTick(date) 
+ }) 
 
# 查看数据静态结构 
> str(head(xs,2)) 
List of 2 
 $ :An ‘xts’ object on 2017-01-01 10:00:00/2017-01-01 10:29:00 containing: 
  Data: num [1:30, 1] 9.98 9.2 10.21 9.08 7.82 ... 
  Indexed by objects of class: [POSIXct,POSIXt] TZ:  
  xts Attributes:   
 NULL 
 $ :An ‘xts’ object on 2017-01-02 10:00:00/2017-01-02 10:29:00 containing: 
  Data: num [1:30, 1] 9.41 13.15 6.07 10.12 10.37 ... 
  Indexed by objects of class: [POSIXct,POSIXt] TZ:  
  xts Attributes:   
 NULL 
 
# 转型为xts类型  
> df<-do.call(rbind.data.frame, xs) 
> xdf<-as.xts(df) 
> head(xdf) 
                       V1 
2017-01-01 10:00:00  9.98 
2017-01-01 10:01:00  9.20 
2017-01-01 10:02:00 10.21 
2017-01-01 10:03:00  9.08 
2017-01-01 10:04:00  7.82 
2017-01-01 10:05:00 10.47 

现在有了数据，那么我们可以对数据日期，按周期的分割了，从而生成开盘价、***价、***价、收盘价。这里一样会用到xts包的函数。关于xts类型的详细介绍，请参考文章 可扩展的时间序列xts。

# 按日进行分割，对应高开低收的价格 
> d1<-to.period(xdf,period='days');head(d1) 
                    xdf.Open xdf.High xdf.Low xdf.Close 
2017-01-01 10:29:00     9.98    13.74    5.35     13.34 
2017-01-02 10:29:00     9.41    13.54    6.07      9.76 
2017-01-03 10:29:00    12.11    13.91    7.16     10.75 
2017-01-04 10:29:00    10.43    14.02    6.31     12.10 
2017-01-05 10:29:00    11.51    13.97    6.67     13.97 
2017-01-06 10:29:00    10.57    12.81    4.30      5.16 
 
# 按月进行分割 
> m1<-to.period(xdf,period='months');m1 
                    xdf.Open xdf.High xdf.Low xdf.Close 
2017-01-31 10:29:00     9.98    16.40    3.85     10.14 
2017-02-28 10:29:00     8.25    16.82    4.17     11.76 
2017-03-31 10:29:00    10.55    15.54    2.77      9.61 
2017-04-30 10:29:00     9.40    16.13    3.84     11.77 
2017-05-31 10:29:00    13.79    16.74    3.97     10.25 
2017-06-30 10:29:00     9.29    16.15    4.38      7.92 
2017-07-31 10:29:00     5.39    16.09    4.55      9.88 
2017-08-31 10:29:00     5.76    16.34    3.27     10.86 
2017-09-30 10:29:00     9.56    16.40    3.58     10.09 
2017-10-31 10:29:00     8.64    15.50    3.23     10.26 
2017-11-30 10:29:00     9.20    15.38    3.00     10.92 
2017-12-27 10:29:00     6.99    16.22    3.87      8.87 
 
# 按7日进行分割 
> d7<-to.period(xdf,period='days',k=7);head(d7) 
                    xdf.Open xdf.High xdf.Low xdf.Close 
2017-01-07 10:29:00     9.98    15.54    4.30     10.42 
2017-01-14 10:29:00    11.38    14.76    5.74      9.17 
2017-01-21 10:29:00     9.57    16.40    3.85     11.91 
2017-01-28 10:29:00    10.51    14.08    4.66     10.97 
2017-02-04 10:29:00    10.43    16.69    4.53      6.09 
2017-02-11 10:29:00    11.98    15.23    5.04     11.57 

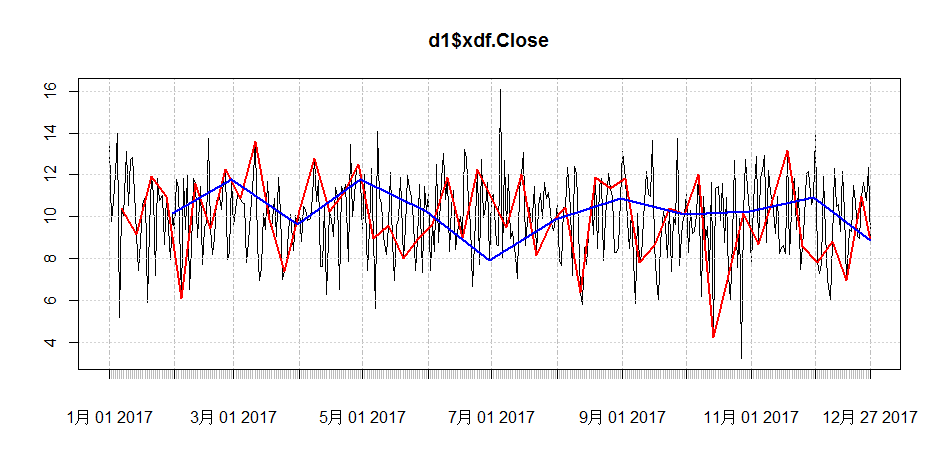
***，通过可视化把不同周期的收盘价，画到一个图中。

> plot(d1$xdf.Close) 
> lines(d7$xdf.Close,col='red',lwd=2) 
> lines(m1$xdf.Close,col='blue',lwd=2) 

从图中，可以看出切换为不同的周期，看到的形状是完全不一样的。黑色线表示以日为周期的，红色线表示以7日为周期的，蓝色线表示以月为周期的。

从本文的介绍来看，要做好数据处理是相当不容易的。你要知道数据是什么样的，业务逻辑是什么，怎么写程序以及数据变形，***怎么进行BI展示，表达出正确的分析维度。试试R语言，忘掉程序员的思维，换成数据的思维，也许繁琐的数据处理工作会让你开心起来。

本文所介绍的数据处理的方法，及个性化的功能函数，我已经发布为一个github的开源项目，项目地址为：https://github.com/bsspirit/RTransform 欢迎大家试用，共同完善。

【作者简介】

[[205144]]

张丹，《R的极客理想》系列图书作者，前况客创始人兼CTO。10年IT编程背景，精通R ,Java, Nodejs 编程，获得10项SUN及IBM技术认证。丰富的互联网应用开发架构经验，金融大数据专家。个人博客 http://fens.me， Alexa全球排名70k。著有《R的极客理想-工具篇》、《R的极客理想-高级开发篇》，合著《数据实践之美》，新书《R的极客理想-量化投资篇》。

【51CTO原创稿件，合作站点转载请注明原文作者和出处为51CTO.com】