最近看到一篇文章 ,写得非常好,在征得作者 Anish 同意的情况下,决定将其翻译成中文。但为了更好理解,一些地方并不会逐字翻译,也会稍作调整。
正确实现一个分布式系统是非常有挑战的一件事情,因为需要很好的处理并发和失败这些问题。网络包可能被延迟,重复,乱序或者丢弃,机器可能在任何时候宕机。即使一些设计被论文证明是正确的,也仍然很难再实现中避免 bug。
除非我们使用形式方法,不然,即使我们假设实现是正确的,我们也需要去测试系统。测试分布式系统也是一件非常有挑战的事情。并发和不确定性使得我们在测试的时候非常难抓住 bug,尤其是在一些极端情况下面才会出现的 bug,譬如同时机器宕机或者极端网络延迟。
正确性
在讨论测试分布式系统的正确性之前,我们首先定义下什么是 “正确性”。即使对于一些简单的系统,要完全的确定系统符合预期也是一件相当复杂的事情。
考虑一个简单的 key-value 系统,譬如 etcd,支持两个操作:Put(key, value) 和 Get(key),首先,我们需要考虑它在顺序情况下面的行为。
顺序规范
通常对于一个 key-value store,我们对于它在顺序操作下面的行为都能有一个直观的认识:Get 操作如果在 Put 的后面,那么一定能得到 Put 的结果。譬如,如果 Put("x", "y") ,那么后面的 Get("x") 就能得到 "y",如果得到了 "z",那么这就是不对的。
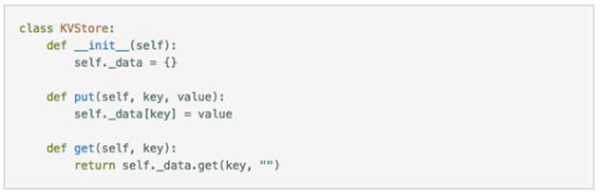
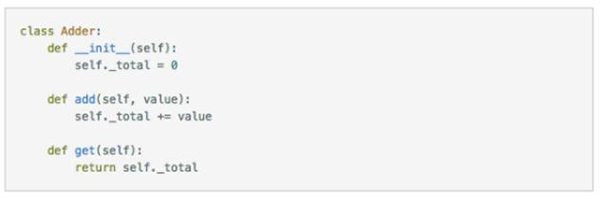
我们使用 Python 定义一个简单的 key-value store:
上面的代码比较简单,但包含了足够的信息,包括初始状态是怎样的,内部状态是如何被操作的结果改变的,从 key-value store 里面操作返回的结果是怎样的。这里需要留意下 Get() 对于不存在的 key 的处理,会返回一个 empty string。
线性一致性
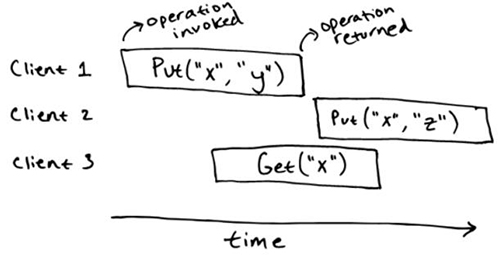
接下来,我们来考虑我们的 key-value store 在并发下面会有怎样的行为。需要注意顺序规范并没有指明在并发操作下面会发生什么。譬如,顺序规范并没有说 key-value store 在下面这个场景下可以允许的操作。
我们并不能立刻知道 Get("x") 这个操作会允许返回怎样的结果。直觉上,我们可以说 Get("x")是跟 Put("x", "y") 和 Put("x", "z") 一起执行的,所以它能可能返回一个值,甚至也可能返回 ""。 如果有另一个 Get("x") 的操作在更后面执行,我们可以说这个一定能返回 "z",因为它是***一次写入的值,而且那个时候并没有其他的并发写入。
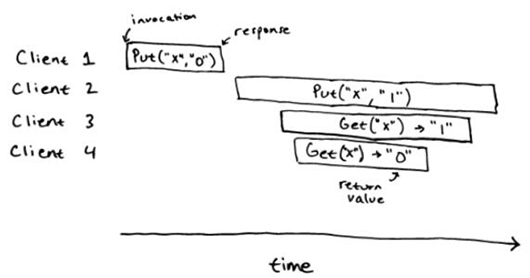
对于一个基于顺序规范的并发操作来说,我们会用一个一致性模型,也就是线性一致性来说明它的正确性。在一个线性一致性的系统里面,任何操作都可能在调用或者返回之间原子和瞬间执行。除了线性一致性,还有一些其他一致性的模型,但多数分布式系统都提供了线性一致性的操作:线性一致性是一个强的一致性模型,并且基于线性一致性系统,很容易去构建其他的系统。考虑到如下对 key-value store 操作的历史例子:
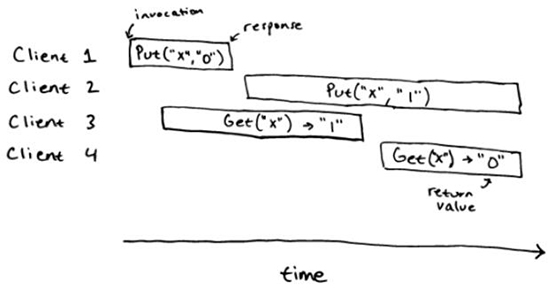
这个历史是一个线性的。在下面图片的蓝色地方,我们现实的标明了线性一致的点。这个顺序历史 Put("x", "0"), Get("x") -> "0", Put("x", "1"), Get("x") -> "1",对于顺序规范来说就是一个正确的历史。
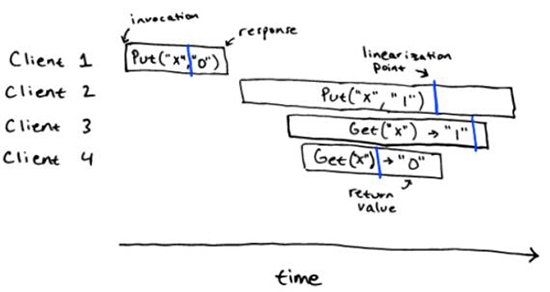
对应的,下面的历史就不是线性一致的。
对于顺序规范来说,这个历史并不是线性一致的:我们并不能在这个历史的操作里面指定出线性一致的点。我们可以画出 client 1,2 和 3 的,但我们并不能画出 client 4 的,因为这明显是一个过期的值。类似的,我们可以画出 client 1,2 和 4 的,那么 client 2 的操作一定会在 4 的操作开始的后面,但这样我们就不能处理 client 3,它只可能合法的返回 "" 或者 "0"。
测试
有了一个正确性的定义,我们就可以考虑如何去测试分布式系统了。通常的做法就是对于正确的操作,不停的进行随机的错误注入,类似机器宕机,网络隔离等。我们甚至能模拟整个网络,这样我们就能做长时间的网络延迟等。因为测试时随机的,我们需要跑很多次从而确定一个系统的实现是正确的。
专门测试
我们实际如何做正确操作的测试呢?在最简单的软件里面,我们可以使用输入输出测试,譬如 assert(expected_output == f(input)),我们也可以在分布式系统上面使用一个类似的方法,譬如,对于 key-value store,当多个 client 开始执行操作的时候,我们可以有如下的测试:
如果测试挂掉了,那么这个系统一定不是线性一致性的,当然,这个测试并不是很完备,因为有可能不是线性一致的系统也可能通过这个测试。
线性一致性
一个更好的办法就是并发的客户端完全跑随机的操作。譬如,循环的去调用 kvstore.put(rand(), rand()) 和 kvstore.get(rand()),有可能会只用很少的 key 去增大冲突的概率。但在这种情况下,我们如何定义什么是正确的操作呢?在上面的简单的测试里面,因为每个 client 都操作的是一个独立的 key,所以我们可以非常明确的知道输出结果。
但是 clients 并发的操作同一堆 keys,事情就变得复杂了。我们并不能预知每个操作的返回值因为这并没样一个唯一的答案。但我们可以用另一个办法:我们可以记录整个操作的历史,然后去验证这个操作历史是线性一致的。
线性一致性验证
一个线性一致性验证器会使用一个顺序规范和一个并发操作的历史,然后执行一个判定程序去检查这个历史在规范下面是否线性一致。
NP 完备
但不幸的是,线性一致性验证是 NP 完备的。这个证明非常简单:我们能说明线性一致性验证是 NP 问题,并且也能展示一个 NP 困难问题能被简化成线性一致性验证。明显的,线性一致性验证是 NP 问题,譬如,所有操作的线性一致性点,根据相关的顺序规范,我们可以在多项式时间里验证。
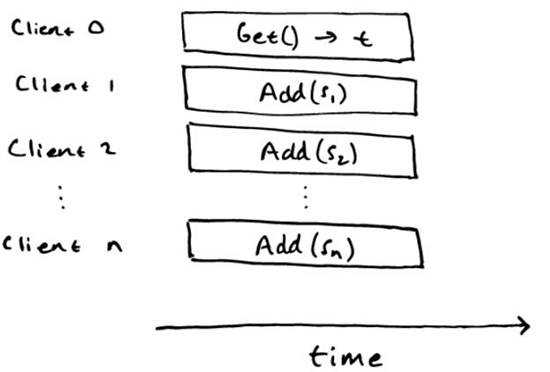
为了说明线性一致性验证是 NP 困难的,我们可以将子集合问题简化成线性一致性验证。对于子集合问题,我们给出非负数的集合 S={s1,s2,…,sn} 和目标结果 t,然后我们必须确定是否存在一个子集 S 的合等于 t。我们可以将这个问题简化成如下的线性一致性验证。考虑顺序规范:
以及历史:
只有在子集合问题的答案是 “yes” 的时候,历史才是线性的。如果历史是线性的,那么我们认为对于任何的 Add(s_i) 操作,在 Get() 操作之前都有线性一致性点,这个就对应了在子集里面 Si,它的合是 t。如果这个集合里面有一个子集的合是 t,我们就能构造一个线性化,它有在 Get 操作发生之前,对应子集 Si 的 Add(s_i) 的操作,也有在 Get() 操作之后其余的操作。
PS:这个章节我大概知道啥意思,但没找到更好的表述来翻译,也就凑合着了。后面再看 paper 来深入了解吧。
实现
即使线性一致性验证是 NP 完全的,在实际中,它仍然能在一些小的历史上面很好的工作。线性一致性验证器的实现会用一个可执行的规范,加上一个历史,执行一个搜索过程去构造一个线性化,并使用一些技巧来限制减少搜索的空间。
在 Jepsen 里面,有一个一致性验证工具 Knossos,但不幸的是,在测试一些分布式 key-value store 的时候,Knossos 并不能很好的工作,它可能只能适用于一些少的并发 clients,以及只有几百的事件的历史。但在一些测试里面,有很多的 clients,以及会生成更多的历史事件。为了解决 Knossos 的问题,作者开发了 Procupine,一个用 Go 写的更快的线性一致性验证工具。Porcupine 使用一个用 Go 开发的执行规范去验证历史是否是线性的。根据实际测试的情况,Porcupine 比 Knossos 快很多倍。
效果
在测试分布式系统的线性一致性的时候,使用错误注入是一个很有效的手段。
作为对比,在使用专门的测试用 Porcupine 测试 key-value store 的时候,作者使用了这两种方式。作者在实现它自己的 key-value store 的时候引入不同的设计错误,譬如在修改之后会出现过期读,来看这些测试是否会挂掉。专门测试会捕捉到很多 bugs,但并没有能力去捕捉到更多的狡猾的 bugs。相对而言,作者现在还没找到一个正确性的 bug 是线性一致性测试不能抓住的。
- 形式方法能够保证一个分布式系统的正确性。例如,UM PLSE 研究小组最近使用 Coq proof assistnt 来验证了 Raft 一致性协议。但不幸的的是,验证需要特定的知识,另外验证实际的系统需要做大量的工作。没准有一天,验证能被用在实际系统上面,但现在,主要还是测试,而不是验证。
- 理论上,所有的生产系统都会有一个形式规范,而且一些系统也已经有了,譬如 Raft 就有一个用 TLA+ 写的形式规范。但不幸的是,大部分的系统是没有的。
【本文是51CTO专栏作者“PingCAP”的原创文章,转载请联系作者本人获取授权】