自动化机器学习第一步：使用Hyperopt自动选择超参数-51CTO.COM

有时候在学习神经网络教程时，我们通常会看到有的实验似乎理所当然地就选定了某种神经网络架构以及特定的网络层数、激活函数、损失函数等等，却没有解释原因。因为解释起来有点难。是的，深度学习社区选择 ReLU(或更现代的选择 ELU 或 SELU)作为激活函数是「常态」，而且我们基本上也欣然接受，但我们通常并没有思考这是否是正确的。比如在网络的层数和优化器的学习率选择上，我们通常都遵循标准。近日，机器学习开发者兼饶舌歌手 Alex Honchar 在 Medium 上发文分享了自动化这些选择过程的方式。另外，本文涉及的相关代码也已在 GitHub 上公开。

代码地址：https://github.com/Rachnog/Deep-Trading/tree/master/hyperparameters

超参数搜索

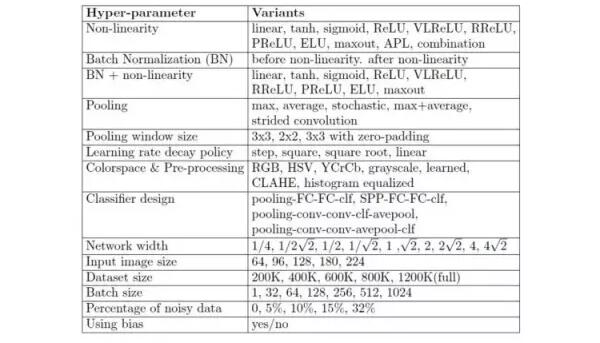
卷积神经网络训练的典型超参数的列表

在开始训练一个模型之前，每个机器学习案例都要选择大量参数;而在使用深度学习时，参数的数量还会指数式增长。在上面的图中，你可以看到在训练计算机视觉卷积神经网络时你要选择的典型参数。

但有一个可以自动化这个选择过程的方法!非常简单，当你要选择一些参数和它们的值时，你可以：

启动网格搜索，尝试检查每种可能的参数组合，当有一种组合优化了你的标准时(比如损失函数达到最小值)，就停止搜索。
当然，在大多数情况下，你可等不了那么久，所以随机搜索是个好选择。这种方法可以随机检查超参数空间，但速度更快而且大多时候也更好。
贝叶斯优化——我们为超参数分布设置一个先决条件，然后在观察不同实验的同时逐步更新它，这让我们可以更好地拟合超参数空间，从而更好地找到最小值。

在这篇文章中，我们将把***一个选项看作是一个黑箱，并且重点关注实际实现和结果分析。

HFT 比特币预测

我使用的数据来自 Kaggle，这是用户 @Zielak 贴出的比特币过去 5 年的每分钟价格数据，数据集地址：

https://www.kaggle.com/mczielinski/bitcoin-historical-data。

比特币价格的样本图

我们将取出其中最近 10000 分钟的一个子集，并尝试构建一个能够基于我们选择的一段历史数据预测未来 10 分钟价格变化的***模型。

对于输入，我想使用 OHLCV 元组外加波动，并将这个数组展开以将其输入多层感知器(MLP)模型。

o = openp[i:i+window] 
h = highp[i:i+window] 
l = lowp[i:i+window] 
c = closep[i:i+window] 
v = volumep[i:i+window] 
volat = volatility[i:i+window] 
x_i = np.column_stack((o, h, l, c, v, volat)) 
x_ix_i = x_i.flatten() 
y_i = (closep[i+window+FORECAST] - closep[i+window]) / closep[i+window]

优化 MLP 参数

我们将使用 Hyperopt 库来做超参数优化，它带有随机搜索和 Tree of Parzen Estimators(贝叶斯优化的一个变体)的简单接口。Hyperopt 库地址：http://hyperopt.github.io/hyperopt

我们只需要定义超参数空间(词典中的关键词)和它们的选项集(值)。你可以定义离散的值选项(用于激活函数)或在某个范围内均匀采样(用于学习率)。

space = {'window': hp.choice('window',[30, 60, 120, 180]), 
        'units1': hp.choice('units1', [64, 512]), 
        'units2': hp.choice('units2', [64, 512]), 
        'units3': hp.choice('units3', [64, 512]), 
        'lr': hp.choice('lr',[0.01, 0.001, 0.0001]), 
        'activation': hp.choice('activation',['relu', 
                                                'sigmoid', 
                                                'tanh', 
                                                'linear']), 
        'loss': hp.choice('loss', [losses.logcosh, 
                                    losses.mse, 
                                    losses.mae, 
                                    losses.mape])}

在我们的案例中，我想检查：

我们需要更复杂还是更简单的架构(神经元的数量)
激活函数(看看 ReLU 是不是真的是***选择)
学习率
优化标准(也许我们可以最小化 logcosh 或 MAE，而不是 MSE)
我们需要的穿过网络的时间窗口，以便预测接下来 10 分钟

当我们用 params 词典的对应值替换了层或数据准备或训练过程的真正参数后(我建议你阅读 GitHub 上的完整代码)：

main_input = Input(shape=(len(X_train[0]), ), name='main_input') 
x = Dense(params['units1'], activation=params['activation'])(main_input) 
x = Dense(params['units2'], activation=params['activation'])(x) 
x = Dense(params['units3'], activation=params['activation'])(x) 
output = Dense(1, activation = "linear", name = "out")(x) 
final_model = Model(inputs=[main_input], outputs=[output]) 
opt = Adam(lr=params['lr']) 
final_model.compile(optoptimizer=opt,  loss=params['loss']) 
history = final_model.fit(X_train, Y_train,  
                  epochs = 5,  
                  batch_size = 256,  
                  verbose=0,  
                  validation_data=(X_test, Y_test), 
                  shuffle=True) 
pred = final_model.predict(X_test) 
predpredicted = pred 
original = Y_test 
mse = np.mean(np.square(predicted - original)) 
sys.stdout.flush()  
return {'loss': -mse, 'status': STATUS_OK}

我们将检查网络训练的前 5 epoch 的性能。在运行了这个代码之后，我们将等待使用不同参数的 50 次迭代(实验)执行完成，Hyperopt 将为我们选出其中***的选择，也就是：

best:  
{'units1': 1, 'loss': 1, 'units3': 0, 'units2': 0, 'activation': 1, 'window': 0, 'lr': 0}

这表示我们需要***两层有 64 个神经元而***层有 512 个神经元、使用 sigmoid 激活函数(有意思)、取经典的学习率 0.001、取 30 分钟的时间窗口来预测接下来的 10 分钟……很好。

结果

首先我们要构建一个「金字塔」模式的网络，我常常用这种模式来处理新数据。大多时候我也使用 ReLU 作为激活函数，并且为 Adam 优化器取标准的学习率 0.002.

X_train, X_test, Y_train, Y_test = prepare_data(60) 
main_input = Input(shape=(len(X_train[0]), ), name='main_input') 
x = Dense(512, activation='relu')(main_input) 
x = Dense(128, activation='relu')(x) 
x = Dense(64, activation='relu')(x) 
output = Dense(1, activation = "linear", name = "out")(x) 
final_model = Model(inputs=[main_input], outputs=[output]) 
opt = Adam(lr=0.002) 
final_model.compile(optoptimizer=opt,  loss=losses.mse)

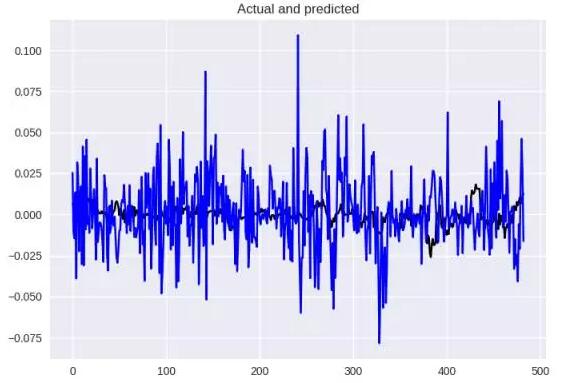
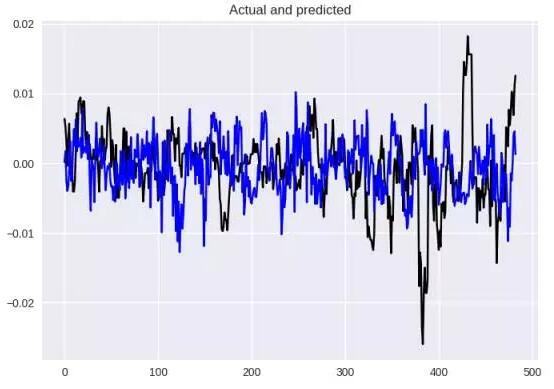
看看表现如何，蓝色是我们的预测，而黑色是原始情况，差异很大，MSE = 0.0005，MAE = 0.017。

基本架构的结果

现在看看使用 Hyperopt 找到的超参数的模型在这些数据上表现如何：

X_train, X_test, Y_train, Y_test = prepare_data(30) 
main_input = Input(shape=(len(X_train[0]), ), name='main_input') 
x = Dense(512, activation='sigmoid')(main_input) 
x = Dense(64, activation='sigmoid')(x) 
x = Dense(64, activation='sigmoid')(x) 
output = Dense(1, activation = "linear", name = "out")(x) 
final_model = Model(inputs=[main_input], outputs=[output]) 
opt = Adam(lr=0.001) 
final_model.compile(optoptimizer=opt, loss=losses.mse)

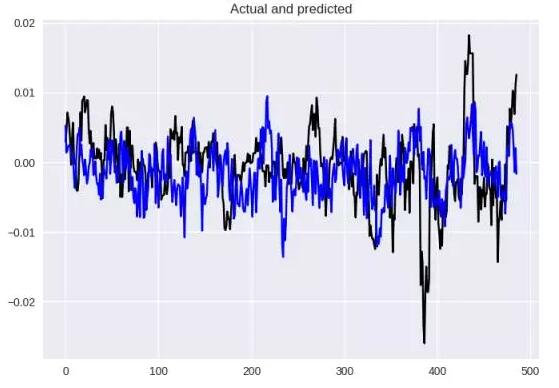
使用 Hyperopt 找的参数所得到的结果

在这个案例中，数值结果(MSE = 4.41154599032e-05，MAE = 0.00507)和视觉效果都好得多。

老实说，我认为这不是个好选择，尤其是我并不同意如此之短的训练时间窗口。我仍然想尝试 60 分钟，而且我认为对于回归而言，Log-Cosh 损失是更加有趣的损失函数选择。但我现在还是继续使用 sigmoid 激活函数，因为看起来这就是表现极大提升的关键。

X_train, X_test, Y_train, Y_test = prepare_data(60) 
main_input = Input(shape=(len(X_train[0]), ), name='main_input') 
x = Dense(512, activation='sigmoid')(main_input) 
x = Dense(64, activation='sigmoid')(x) 
x = Dense(64, activation='sigmoid')(x) 
output = Dense(1, activation = "linear", name = "out")(x) 
final_model = Model(inputs=[main_input], outputs=[output]) 
opt = Adam(lr=0.001) 
final_model.compile(optoptimizer=opt,  loss=losses.logcosh)

这里得到 MSE = 4.38998280095e-05 且 MAE = 0.00503，仅比用 Hyperbot 的结果好一点点，但视觉效果差多了(完全搞错了趋势)。

结论

我强烈推荐你为你训练的每个模型使用超参数搜索，不管你操作的是什么数据。有时候它会得到意料之外的结果，比如这里的超参数(还用 sigmoid?都 2017 年了啊?)和窗口大小(我没料到半小时的历史信息比一个小时还好)。

如果你继续深入研究一下 Hyperopt，你会看到你也可以搜索隐藏层的数量、是否使用多任务学习和损失函数的系数。基本上来说，你只需要取你的数据的一个子集，思考你想调节的超参数，然后等你的计算机工作一段时间就可以了。这是自动化机器学习的***步!

原文：

https://medium.com/@alexrachnog/neural-networks-for-algorithmic-trading-hyperparameters-optimization-cb2b4a29b8ee

【本文是51CTO专栏机构“机器之心”的原创译文，微信公众号“机器之心( id: almosthuman2014)”】

戳这里，看该作者更多好文