一个古老的诅咒一直萦绕着数据分析:我们用来改进模型的变量越多,那么我们需要的数据就会出现指数级的增长。不过,我们通过关注重要的变量就可以避免欠拟合以及降低收集大量数据的需求。减少输入变量的一种方法是鉴别其对输出变量的影响。变量的相关性有助于这种鉴别:如果相关性较强,那么输入变量的一个显著变化将会导致输出变量同等程度的变化。我们要选择跟模型的输出变量强相关的输入变量,而不是使用所有的可用变量。
然而当输入变量之间存在强相关性时,这里就会出现一个陷阱。假设想预测一下父母的教育水平,我们发现在我们的数据集中的乡间俱乐部会员资格、家庭汽车数量以及度假费用之间有很强的相关性。拥有所有这些奢侈品的家庭都有相同的特征:家庭富有。所以真正的根本关联是受过高等教育的父母通常有较高的收入。我们可以使用家庭收入来预测父母的教育水平,或者使用上面的变量数组。我们称这种相关为“组间相关”
组间相关是解释性变量之间的相关性。添加足够多的变量时,会引起维度灾难并需要大量的数据。所以有时从一组组间相关的输入变量中选择一个代表变量是有好处的。在本文中我们会利用新创造的可视化方法“太阳系相关图”来探讨相关性和组间相关性,并展示如何轻松地创建一个你自己的太阳系相关图。
把太阳系相关图应用于房价数据
我们可以使用协方差和系数矩阵将太阳系相关图应用于房价数据。尽管这些工具同样有效,但很难理解。幸运的是这些矩阵可以通过精美简洁的可视化展示来探索相关性。
太阳系相关图是为了解决以下两个需求而设计的:
- 每个输入变量与输出变量的相关性的可视化展示
- 输入变量的组间相关性
我们来探索一个标准数据集并生成其太阳系相关图。卡内基梅隆大学收集了上世纪九十年代的波士顿房价数据,它是UCI(加利福尼亚大学尔湾分校)机器学习资源库中可免费访问的数据集之一。我们使用这个数据集的目标是利用数据集中的几个输入变量来预测输出变量——房屋价值(MEDV)。
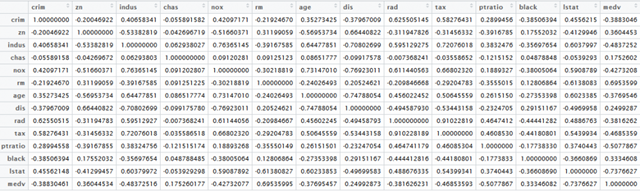
首先我们生成一个相关矩阵:
图1 来源:Stefan Zapf和Christopher Kraushaar
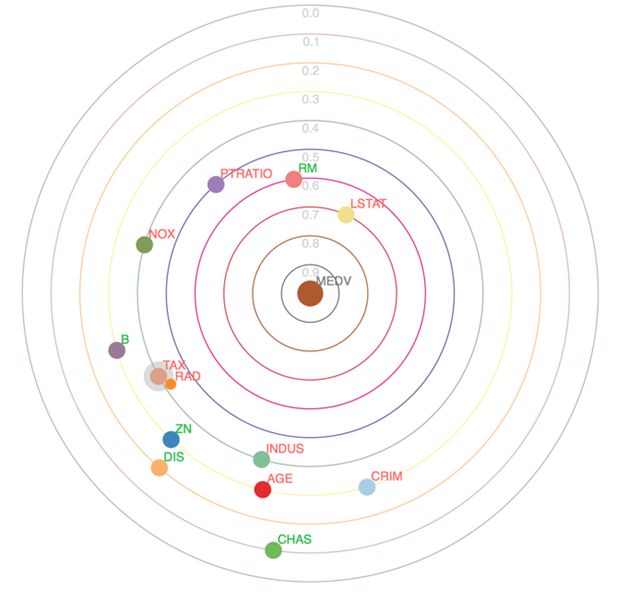
你可以通过搜索MEDV行和TAX列交叉的单元格得到输出变量(房屋价值)和输入变量(税收)的相关性。为了探讨组间相关性,你需要找到绝对值大于某个值(比如0.8)的所有单元格。在复杂的数据集中,搞懂大量的单元格数值需要很长的时间。而太阳系相关图可以帮助你理解这些数值。我们会先从输入变量与输出变量的相关性开始。以下是用太阳系相关图表示的房价信息概要:
图2 来源:Stefan Zapf和Christopher Kraushaar
输出变量MEDV(波士顿的房价)是太阳系中心的太阳。太阳周围的每一圈都是轨道。行星是输入变量,卫星是与它围绕旋转的行星有相互关联的输入变量。轨道越近的行星跟太阳的相关性越强。例如第二个轨道是代表较低收入邻居(LSTAT)的行星、第三个轨道的行星代表房屋房间的数量(RM)、第四个轨道的行星代表了房屋的大小(PTRATIO)。房屋面积、房间数量以及居民的潜在购买力很大程度上决定了房屋的价值。我们并不是想选一个会让你吃惊的例子。恰恰相反,变量的常识分析会有助于我们认识到太阳系相关图的有效性。
相关性的强度取决于Pearson相关系数的绝对值大小。***个轨道行星的相关系数绝对值为0.9-1.0。第二轨道行星的相关系数绝对值为0.8-0.9,依此类推。另一个指示是行星的颜色和大小。太阳是一个大圆圈,行星是中等大小的圆圈而卫星是小圆圈。
探索组间相关的输入变量
你可能注意到太阳系里没有太多行星有卫星。我们将多变量组间相关的阈值设置为默认值,即Pearson相关系数必须大于0.8。通常强相关性要Pearson系数高于0.5。设置默认值是非常谨慎的,但您可以在相关性分析中调整该数字。如果我们有相互关联的变量,那么跟输出变量最相关的输入变量作为行星,而其他变量则是它的卫星。这是为了确保行星是最能解释输出变量的输入变量。
在我们的例子中,只有两个变量是强烈地相关以至于几乎相同。并不是每个太阳系里都只有很少的卫星。在大数据环境中,太阳系相关图中通常有更多的变量(且附带有许多卫星)。随着变量数量的增加,太阳系相关图会变得更加重要。
现在我们来看一下输入变量之间的相互关联问题。在第六个绿色的轨道上有一个行星附带一个卫星。行星代表的变量是房地产税率(TAX),卫星代表的是到达高速公路的便利性(RAD)。由于住宅和商业地产的税率不同,行星变量可能是个区分商业区和住宅区的指标。企业通常希望能快速进入高速公路,而私人住宅房主通常希望避免高速公路的噪音和空气污染。一个街区的商业或住宅性质很可能是这些变量相互关联的根本原因。如果是这种情况,那么就需要保留其中一个最能解释对房价影响的变量。
谨慎的意思是符合程序的。数据分析不是机械性或确定性的过程。例如即使是富裕的家庭可能也不会购买跑车,因为他们关心环境污染。因此当我们试图预测家庭财富时,我们可能会观测到跑车变量在一个偏远的轨道上,这表明跑车不是财富的良好指标。但是我们知道拥有跑车是财富的一个很好的指标。没有选择跑车作为财富的指标是因为它是一个偏远的行星,这肯定是错误的策略,因为一个复杂的模型可以调节其关于家庭对环境的态度的影响。相关性是一个很有用的工具,但常常需要权衡结果和你的常识,并相信你的直觉,这其中包含大量的假设检验和贝叶斯分析。
在探索性数据分析(EDA)和建模时,太阳系相关图可以帮助我们通过视觉方式理解相关性。对相关性的理解可以作为我们选择建模变量优先级的基础:低轨道的行星是***的候选项,下一个是卫星,***是最外面轨道的行星。
正面和负面的标签
到目前为止,我们已经解释了相关性的强度和重要性。然而,我们也想知道一个相关是正相关还是负相关?正相关意味着一个变量增加时另一个也增加。这是“越多越好”的相关性。我们先来看一下变量RM,它是房间的平均数量。房子的房间越多房价就越高,这表明房子更大以及房子空间更容易分隔。当我们有十个房间而不是两个房间时,房子可能会有更高的价格。这是正相关的本质。你可以看到MEDV和RM之间的为相关性为正,因为标签RM为绿色。
负相关意味着一个变量增加时另一个变量会降低:“有时少即是多”变量。犯罪率越低,我们的房子的价格会越高,所以我们猜想犯罪的标签是红色的。我们的猜想在太阳系相关图中被证明是正确的。
通过太阳系相关图,我们可以一目了然地看到强度、相关性和相关性的类型。
如何简单地创建一个太阳系相关图
太阳系相关图的创建跟烘烤冷冻曲奇饼面团一样简单。 它是一个可以使用pip安装的Python模块:pip install solar-correlation-map。 然后,尝试从我们的GitHub资源上下载jedi.csv文件。这个文件是自带表头的标准csv文件:
图3 来源:Stefan Zapf和Christopher Kraushaar
这个数据集是关于绝地武士的变量数据:
- JEDI:变量越大,绝地武士就越靠近光明面
- GRAMMAR:越高的值表示一个绝地武士有越好的语法
- GREENESS:变量越高,皮肤越绿
- IMPLANTS:体内植入物的数量
- ELEGEN:原力者可以通过的电能的兆焦耳量
- MIDI-CHLORIANS:血液中的纤原体数量
- FRIENDS:朋友的数量
请注意在这个名单中的所有人的纤原体数量都是相同的。看来我们选择了相当强大的原力使用者。
然后使用以下命令在你下载的jedi-csv文件所在的目录中运行太阳系相关图:
- winterfell:solar-correlation-map daebwae$ python -m solar_correlation_map jedi.csv JEDI
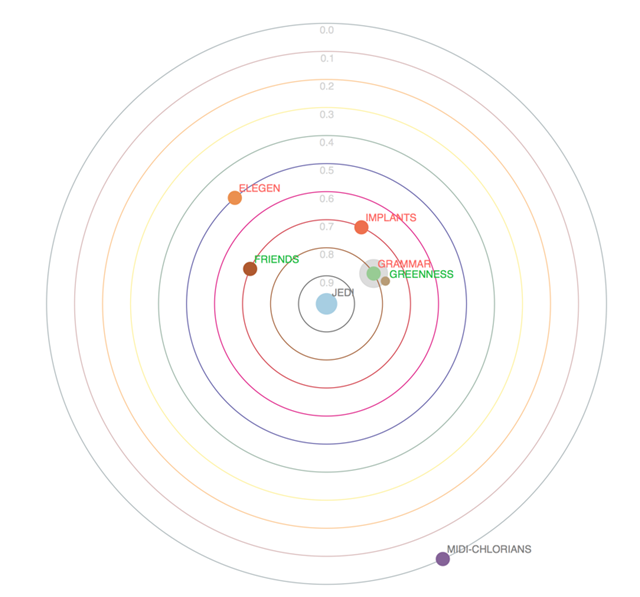
此时在你的屏幕上,会出现一个包含太阳系相关图的窗口:
图4 来源:Stefan Zapf和Christopher Kraushaar
语法(GRAMMAR)在一个很近的轨道上且标签是红色的,所以语法(GRAMMAR)和绝地武士(Jedi)之间有很强的负相关关系。语法越好这个人就越不可能是个绝地武士。 另外绿色(GREENESS)与不良语法(GRAMMA)相关联,所以两者都可能跟潜在的相同因素相关联。记住所有人都有非常相似的纤原体数量(MIDI-CHLORIANS)。因此它不可能告诉我们有关原力者是否是绝地战士的任何事情。这就是为什么纤原体数量(MIDI-CHLORIANS)在最外面的轨道。
三个步骤实现一个新的可视化
我们已经介绍了太阳系相关图,让我们回顾一下这张图。我们从数据分析问题出发,找出对输出变量影响***的输入变量。我们可以用相关矩阵的工具来分析这个问题。通过视觉总结这个问题有助于找到相互关联和最有影响力的输入变量。由于可视化跟信息传达是息息相关的,所以我们选择了广大读者都熟悉的太阳系做类比。
以下是实现一个新的可视化的三个步骤:
- 识别数据分析中的问题
- 找到解决这个问题的分析工具
- 使用视觉类比来探索和展现你的结果
古往今来讲故事的人都具有创造性和勇气,数据分析往往就像讲故事一样。同样地,数据科学家可以追随过去讲故事的人的足迹,大胆地探索新的方式来向读者传达数据的故事。
在探索性数据分析中,我们的可视化工具箱在沟通和说服方面发挥着重要的作用。本文介绍了太阳系相关图,并把它作为对这个过程的一个高级抽象,来创建可以解决实际探索性数据分析问题的新型可视化方法。当你在讲述数据的故事时,你可以探索读者未曾看过的新奇的可视化世界。让你的新奇创意吸引读者并帮助扩展数据科学家的视觉类比方法。