今天来介绍一个小项目:在TensorFlow中生成分形图案。分形本身只是一个数学概念,与机器学习并无太大关系,但是通过分形的生成,我们可以了解怎么在TensorFlow中进行数学计算,以及如何进行基本的流程控制,是学习TensorFlow的一个非常好的练手项目。
在开始之前,需要说明的是,TensorFlow官方也提供了一个生成分形图案的教程(地址: www.tensorflow.org/tutorials/mandelbrot),然而官方教程中生成的图像实在是太丑了,而且只能生成一种图案,我对官方的代码做了一些改进,并且加入了多种类型的分形,此外,不仅可以生成图像,还可以制作gif动画,代码已经放到了Github上:hzy46/tensorflow-fractal-playground,主要的程序只有50行,欢迎大家参考。
Mandelbrot集合
Mandelbrot集合是分形中最经典的一个例子。考虑迭代公式z_{n+1}=z_{n}^2 + c(z和c都是复数)。当z_0为0时,得到的值可以组成一个数列,依次为c, c^2+c,(c^2+c)^2+c……。当该数列发散到无穷时,对应的点就属于Mandelbrot集合。
如c=0 时,显然数列永远是0,并不发散,因此0不属于Mandelbrot集合。
又如c=3i 时,对应的数列为3i, -9+3i, 63-51i, 1431-6477j…. ,数字越来越庞大,因此3i就属于Mandelbrot集合。
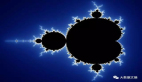
在二维平面上,将所有不属于Mandelbrot集合的点标记为黑色,将所有属于Mandelbrot集合的点按照其发散速度赋予不同的颜色,就可以得到Mandelbrot的经典图像:
上面这张图完全是使用TensorFlow进行计算的,类似的图大家应该在网上也见过好多了,在TensorFlow中,我们定义下面的计算步骤:
- xs = tf.constant(Z.astype(np.complex64))
- zs = tf.Variable(xs)
- ns = tf.Variable(tf.zeros_like(xs, tf.float32)) with tf.Session():
- tf.global_variables_initializer().run()
- zs_ = tf.where(tf.abs(zs) < R, zs**2 + xs, zs)
- not_diverged = tf.abs(zs_) < R
- step = tf.group(
- zs.assign(zs_),
- ns.assign_add(tf.cast(not_diverged, tf.float32))
- for i in range(ITER_NUM): step.run()
- final_step = ns.eval()
- final_z = zs_.eval()
zs就对应我们之前迭代公式的z,而xs就对应迭代公式中的c。为了方便起见,只要计算时数值的绝对值大于一个事先指定的值R,就认为其发散。每次计算使用tf.where只对还未发散的值进行计算。结合ns和zs_就可以计算颜色,得到经典的Mandelbrot图像。
Julia集合
Julia集合和Mandelbrot集合差不多,但这次我们固定c,转而计算发散的z的值。即c是固定的常数(可以任取),数列变成z,z^2+c,(z^2+c)^2 +c,…..。如果该数列发散,对应的z就属于Julia集合。对此,我们只要在原来的程序中修改两行内容,就可以生成Julia集合:
- xs = tf.constant(np.full(shape=Z.shape, fill_value=c, dtype=Z.dtype))
- zs = tf.Variable(Z)
我们在fill_value=c处指定了Julia集合中的c值,只要使用不同的c值,就可以生成完全不同的Julia集合!
默认:c = -0.835 – 0.2321i :
将c值变为c = -0.8 * 1j ,并调整颜色(调整方法参考Github页面的说明):
选用c=0.285 + 0.01i ,图案又变得完全不同:
生成Julia集合的动画
在Julia集合中,每次都对c的值进行微小的改变,并将依次生成图片制作为gif,就可以生成如下所示的动画,对应的代码为julia_gif.py:
这里由于上传gif有大小限制的关系,只展示了一个小尺寸的动画图像。程序中提供了一个width参数,可以修改它以生成更大尺寸,质量更高的动画图像。
探索Mandelbrot集合
(注意:下面的图片可能对密集恐惧症患者不太友好。。。因此慎重翻页。。)
在前面生成的Mandelbrot集合中,我们可以将图像放大,选取某些区域进行生成,就可以得到格式各样造型迥异的分形图案,对应的程序为mandelbrot_area.py。
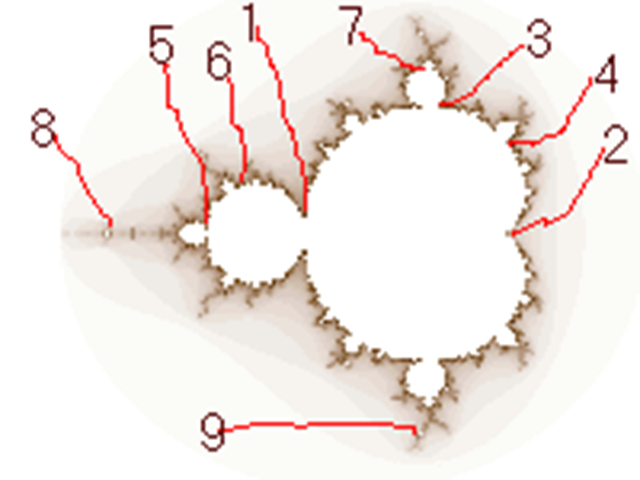
在Mandelbrot集合中,有很多地方图案比较奇特,如下图中的9个位置。
其中编号为2的地方被称为“Elephant Valley”,因为此处的图案与大象很像,直接运行mandelbrot_area.py就可以得到该区域的图像:
编号为3的地方被称为“Triple Spiral Valley”(三重螺旋),在mandelbrot_area.py修改一下坐标位置为(ratio调整的是颜色):
- start_x = -0.090 # x range
- end_x = -0.086
- start_y = 0.654 # y range
- end_y = 0.657
- width = 1000
- ratio1, ratio2, ratio3 = 0.2, 0.6, 0.6
就可以得到该处的图案:
***编号为1的地方被称为“Seahorse Valley”(海马山谷),对应的坐标为:
- start_x = -0.750 # x range
- end_x = -0.747
- start_y = 0.099 # y range
- end_y = 0.102
- width = 1000
- ratio1, ratio2, ratio3 = 0.1, 0.1, 0.3
图像如下,确实和海马有一点神似:
生成更多的图案
项目提供了两个jupyter notebook:Mandelbrot.ipynb和Julia.ipynb可以对Mandelbrot集合、Julia集合做更方便的探索。其中,Mandelbrot集的更多坐标位置可以参考Quick Guide to the Mandelbrot Set,Julia集中更多有趣的c值可以参考Julia set – Wikipedia。网上类似的资源还有很多。
***再安利一下项目地址:hzy46/tensorflow-fractal-playground。如果代码有什么问题可以直接发在评论里或者在Github上提出issue:)