前段时间连续上了一个月班,加班加点完成了一个3D攻坚项目。也算是由传统web转型到webgl图形学开发中,坑不少,做了一下总结分享。
1、法向量问题
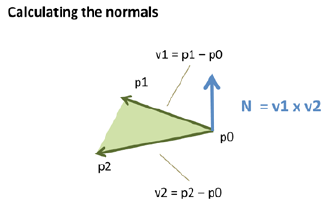
法线是垂直于我们想要照亮的物体表面的向量。法线代表表面的方向因此他们为光源和物体的交互建模中具有决定性作用。每一个顶点都有一个关联的法向量。
如果一个顶点被多个三角形共享,共享顶点的法向量等于共享顶点在不同的三角形中的法向量的和。N=N1+N2;
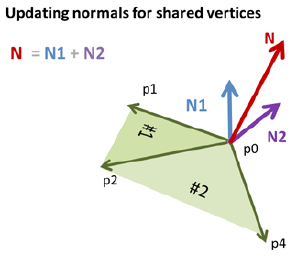
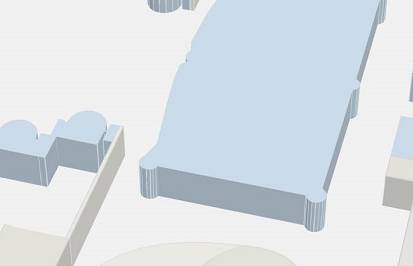
所以如果不做任何处理,直接将3维物体的点传递给BufferGeometry,那么由于法向量被合成,经过片元着色器插值后,就会得到这个黑不溜秋的效果
我的处理方式使顶点的法向量保持唯一,那么就需要在共享顶点处,拷贝一份顶点,并重新计算索引,是的每个被多个面共享的顶点都有多份,每一份有一个单独的法向量,这样就可以使得每个面都有一个相同的颜色
2、光源与面块颜色
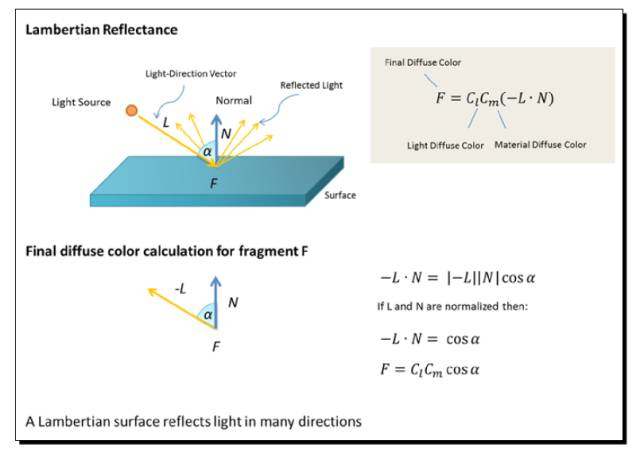
开发过程中设计给了一套配色,然而一旦有光源,面块的最终颜色就会与光源混合,颜色自然与最终设计的颜色大相径庭。下面是Lambert光照模型的混合算法。
而且产品的要求是顶面保持设计的颜色,侧面需要加入光源变化效果,当对地图做操作时,侧面颜色需要根据视角发生变化。那么我的处理方式是将顶面与侧面分别绘制(创建两个Mesh),顶面使用MeshLambertMaterial的emssive属性设置自发光颜色与设计颜色保持一致,也就不会有光照效果,侧面综合使用Emssive与color来应用光源效果。
3、POI标注
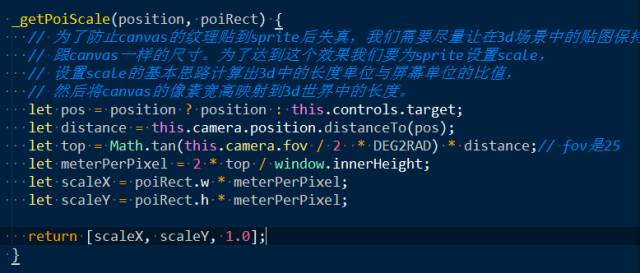
Three中创建始终朝向相机的POI可以使用Sprite类,同时可以将文字和图片绘制在canvas上,将canvas作为纹理贴图放到Sprite上。但这里的一个问题是canvas图像将会失真,原因是没有合理的设置sprite的scale,导致图片被拉伸或缩放失真。
问题的解决思路是要保证在3d世界中的缩放尺寸,经过一系列变换投影到相机屏幕后仍然与canvas在屏幕上的大小保持一致。这需要我们计算出屏幕像素与3d世界中的长度单位的比值,然后将sprite缩放到合适的3d长度。
4、点击拾取问题
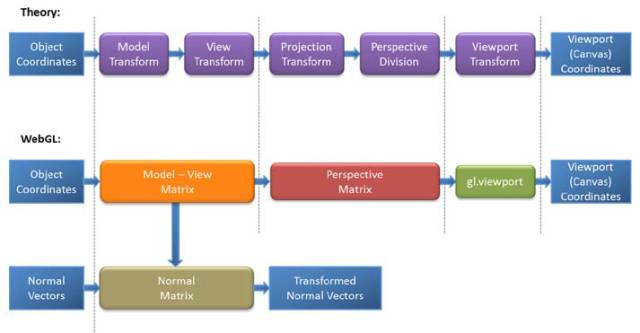
webgl中3D物体绘制到屏幕将经过以下几个阶段
所以要在3D应用做点击拾取,首先要将屏幕坐标系转化成ndc坐标系,这时候得到ndc的xy坐标,由于2d屏幕并没有z值所以,屏幕点转化成3d坐标的z可以随意取值,一般取0.5(z在-1到1之间)。
- function fromSreenToNdc(x, y, container) {
- return {
- x: x / container.offsetWidth * 2 - 1,
- y: -y / container.offsetHeight * 2 + 1,
- z: 1
- };
- }
- function fromNdcToScreen(x, y, container) {
- return {
- x: (x + 1) / 2 * container.offsetWidth,
- y: (1 - y) / 2 * container.offsetHeight
- };
- }
然后将ndc坐标转化成3D坐标:
- ndc = P * MV * Vec4
- Vec4 = MV-1 * P -1 * ndc
这个过程在Three中的Vector3类中已经有实现:
- unproject: function () {
- var matrix = new Matrix4();
- return function unproject( camera ) {
- matrix.multiplyMatrices( camera.matrixWorld, matrix.getInverse( camera.projectionMatrix ) );
- return this.applyMatrix4( matrix );
- };
- }(),
将得到的3d点与相机位置结合起来做一条射线,分别与场景中的物体进行碰撞检测。首先与物体的外包球进行相交性检测,与球不相交的排除,与球相交的保存进入下一步处理。将所有外包球与射线相交的物体按照距离相机远近进行排序,然后将射线与组成物体的三角形做相交性检测。求出相交物体。当然这个过程也由Three中的RayCaster做了封装,使用起来很简单:
- mouse.x = ndcPos.x;
- mouse.y = ndcPos.y;
- this.raycaster.setFromCamera(mouse, camera);
- var intersects = this.raycaster.intersectObjects(this._getIntersectMeshes(floor, zoom), true);
5、性能优化
随着场景中的物体越来越多,绘制过程越来越耗时,导致手机端几乎无法使用。
在图形学里面有个很重要的概念叫“one draw all”一次绘制,也就是说调用绘图api的次数越少,性能越高。比如canvas中的fillRect、fillText等,webgl中的drawElements、drawArrays;所以这里的解决方案是对相同样式的物体,把它们的侧面和顶面统一放到一个BufferGeometry中。这样可以大大降低绘图api的调用次数,极大的提升渲染性能。
这样解决了渲染性能问题,然而带来了另一个问题,现在是吧所有样式相同的面放在一个BufferGeometry中(我们称为样式图形),那么在面点击时候就无法单独判断出到底是哪个物体(我们称为物体图形)被选中,也就无法对这个物体进行高亮缩放处理。我的处理方式是,把所有的物体单独生成物体图形保存在内存中,做面点击的时候用这部分数据来做相交性检测。对于选中物体后的高亮缩放处理,首先把样式面中相应部分裁减掉,然后把选中的物体图形加入到场景中,对它进行缩放高亮处理。裁剪方法是,记录每个物体在样式图形中的其实索引位置,在需要裁切时候将这部分索引制零。在需要恢复的地方在把这部分索引恢复成原状。
6、面点击移动到屏幕中央
这部分也是遇到了不少坑,首先的想法是:
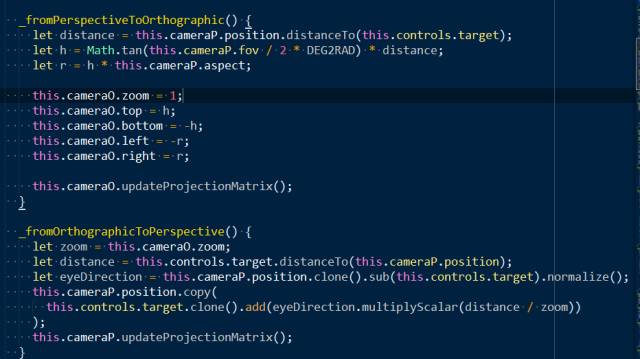
面中心点目前是在世界坐标系内的坐标,先用center.project(camera)得到归一化设备坐标,在根据ndc得到屏幕坐标,而后根据面中心点屏幕坐标与屏幕中心点坐标做插值,得到偏移量,在根据OribitControls中的pan方法来更新相机位置。这种方式最终以失败告终,因为相机可能做各种变换,所以屏幕坐标的偏移与3d世界坐标系中的位置关系并不是线性对应的。
最终的想法是:
我们现在想将点击面的中心点移到屏幕中心,屏幕中心的ndc坐标永远都是(0,0)我们的观察视线与近景面的焦点的ndc坐标也是0,0;也就是说我们要将面中心点作为我们的观察点(屏幕的中心永远都是相机的观察视线),这里我们可以直接将面中心所谓视线的观察点,利用lookAt方法求取相机矩阵,但如果这样简单处理后的效果就会给人感觉相机的姿态变化了,也就是会感觉并不是平移过去的,所以我们要做的是保持相机当前姿态将面中心作为相机观察点。
回想平移时我们将屏幕移动转化为相机变化的过程是知道屏幕偏移求target,这里我们要做的就是知道target反推屏幕偏移的过程。首先根据当前target与面中心求出相机的偏移向量,根据相机偏移向量求出在相机x轴和up轴的投影长度,根据投影长度就能返推出应该在屏幕上的平移量。
- this.unprojectPan = function(deltaVector, moveDown) {
- // var getProjectLength()
- var element = scope.domElement === document ? scope.domElement.body : scope.domElement;
- var cxv = new Vector3(0, 0, 0).setFromMatrixColumn(scope.object.matrix, 0);// 相机x轴
- var cyv = new Vector3(0, 0, 0).setFromMatrixColumn(scope.object.matrix, 1);// 相机y轴
- // 相机轴都是单位向量
- var pxl = deltaVector.dot(cxv)/* / cxv.length()*/; // 向量在相机x轴的投影
- var pyl = deltaVector.dot(cyv)/* / cyv.length()*/; // 向量在相机y轴的投影
- // offset=dx * vector(cx) + dy * vector(cy.project(xoz).normalize)
- // offset由相机x轴方向向量+相机y轴向量在xoz平面的投影组成
- var dv = deltaVector.clone();
- dv.sub(cxv.multiplyScalar(pxl));
- pyl = dv.length();
- if ( scope.object instanceof PerspectiveCamera ) {
- // perspective
- var position = scope.object.position;
- var offset = new Vector3(0, 0, 0);
- offset.copy(position).sub(scope.target);
- var distance = offset.length();
- distance *= Math.tan(scope.object.fov / 2 * Math.PI / 180);
- // var xd = 2 * distance * deltaX / element.clientHeight;
- // var yd = 2 * distance * deltaY / element.clientHeight;
- // panLeft( xd, scope.object.matrix );
- // panUp( yd, scope.object.matrix );
- var deltaX = pxl * element.clientHeight / (2 * distance);
- var deltaY = pyl * element.clientHeight / (2 * distance) * (moveDown ? -1 : 1);
- return [deltaX, deltaY];
- } else if ( scope.object instanceof OrthographicCamera ) {
- // orthographic
- // panLeft( deltaX * ( scope.object.right - scope.object.left ) / scope.object.zoom / element.clientWidth, scope.object.matrix );
- // panUp( deltaY * ( scope.object.top - scope.object.bottom ) / scope.object.zoom / element.clientHeight, scope.object.matrix );
- var deltaX = pxl * element.clientWidth * scope.object.zoom / (scope.object.right - scope.object.left);
- var deltaY = pyl * element.clientHeight * scope.object.zoom / (scope.object.top - scope.object.bottom);
- return [deltaX, deltaY];
- } else {
- // camera neither orthographic nor perspective
- console.warn( 'WARNING: OrbitControls.js encountered an unknown camera type - pan disabled.' );
- }
- }
7、2/3D切换
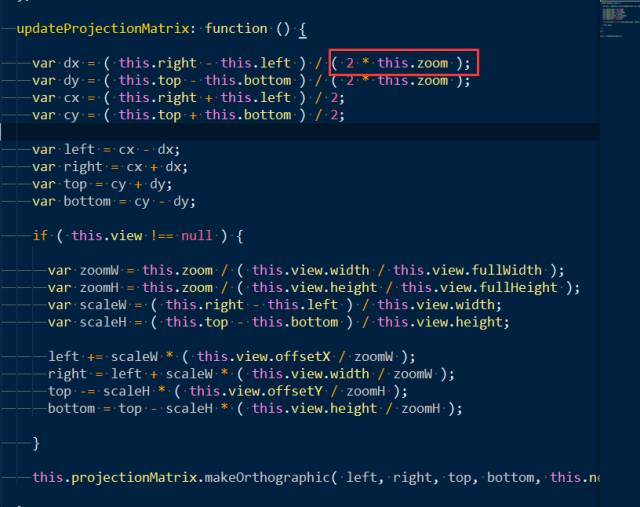
23D切换的主要内容就是当相机的视线轴与场景的平面垂直时,使用平行投影,这样用户只能看到顶面给人的感觉就是2D视图。所以要根据透视的视锥体计算出平行投影的世景体。
因为用户会在2D、3D场景下做很多操作,比如平移、缩放、旋转,要想无缝切换,这个关键在于将平行投影与视锥体相机的位置、lookAt方式保持一致;以及将他们放大缩小的关键点:distance的比例与zoom来保持一致。
平行投影中,zoom越大代表六面体的首尾两个面面积越小,放大越大。
8、3D中地理级别
地理级别实际是像素跟墨卡托坐标系下米的对应关系,这个有通用的标准以及计算公式:
- r=6378137
- resolution=2*PI*r/(2^zoom*256)
各个级别中像素与米的对应关系如下:
- resolution zoom 2048 blocksize 256 blocksize scale(dpi=160)
- 156543.0339 0 320600133.5 40075016.69 986097851.5
- 78271.51696 1 160300066.7 20037508.34 493048925.8
- 39135.75848 2 80150033.37 10018754.17 246524462.9
- 19567.87924 3 40075016.69 5009377.086 123262231.4
- 9783.939621 4 20037508.34 2504688.543 61631115.72
- 4891.96981 5 10018754.17 1252344.271 30815557.86
- 2445.984905 6 5009377.086 626172.1357 15407778.93
- 1222.992453 7 2504688.543 313086.0679 7703889.465
- 611.4962263 8 1252344.271 156543.0339 3851944.732
- 305.7481131 9 626172.1357 78271.51696 1925972.366
- 152.8740566 10 313086.0679 39135.75848 962986.1831
- 76.4370283 11 156543.0339 19567.87924 481493.0916
- 38.2185141 12 78271.51696 9783.939621 240746.5458
- 19.1092571 13 39135.75848 4891.96981 120373.2729
- 9.5546285 14 19567.87924 2445.984905 60186.63645
- 4.7773143 15 9783.939621 1222.992453 30093.31822
- 2.3886571 16 4891.96981 611.4962263 15046.65911
- 1.1943286 17 2445.984905 305.7481131 7523.329556
- 0.5971643 18 1222.992453 152.8740566 3761.664778
- 0.2985821 19 611.4962263 76.43702829 1880.832389
- 0.1492911 20 305.7481131 38.21851414 940.4161945
- 0.0746455 21
- 0.0373227 22
3D中的计算策略是,首先需要将3D世界中的坐标与墨卡托单位的对应关系搞清楚,如果已经是以mi来做单位,那么就可以直接将相机的投影屏幕的高度与屏幕的像素数目做比值,得出的结果跟上面的ranking做比较,选择不用的级别数据以及比例尺。注意3D地图中的比例尺并不是在所有屏幕上的所有位置与现实世界都满足这个比例尺,只能说是相机中心点在屏幕位置处的像素是满足这个关系的,因为平行投影有近大远小的效果。
9、poi碰撞
由于标注是永远朝着相机的,所以标注的碰撞就是把标注点转换到屏幕坐标系用宽高来计算矩形相交问题。至于具体的碰撞算法,大家可以在网上找到,这里不展开。下面是计算poi矩形的代码