基于 boosting 原理训练深层残差神经网络-深度残差神经网络

1. 背景

1.1 Boosting

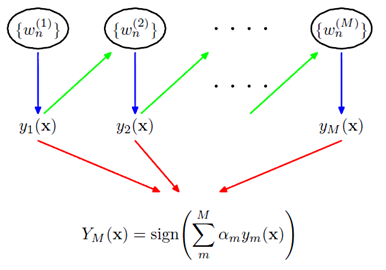
Boosting[1] 是一种训练 Ensemble 模型的经典方法，其中一种具体实现 GBDT 更是广泛应用在各类问题上。介绍boost的文章很多，这里不再赘述。简单而言，boosting 方法是通过特定的准则，逐个训练一系列弱分类，这些弱分类加权构成一个强分类器（图1）。

1.2 残差网络

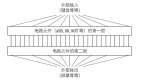
残差网络[2]目前是图像分类等任务上***的模型，也被应用到语音识别等领域。其中核心是 skip connect 或者说 shortcut（图2）。这种结构使梯度更易容向后传导，因此，使训练更深的网络变得可行。

在之前的博文作为 Ensemble 模型的 Residual Network中，我们知道，一些学者将残差网络视一种特殊的 Ensemble 模型[3,4]。论文作者之一是Robert Schapire（刚注意到已经加入微软研究院），AdaBoost的提出者（和 Yoav Freund一起）。Ensemble 的观点基本算是主流观点（之一）了。

2. 训练方法

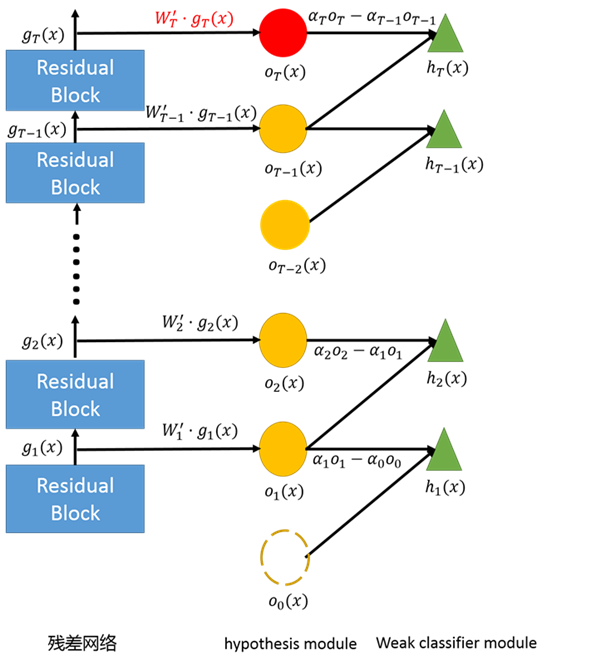
2.1 框架

残差网络

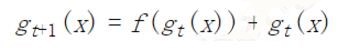
即这是一个线性分类器（Logistic Regression）。

hypothesis module

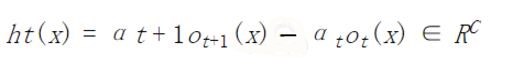
其中 $C$ 为分类任务的类别数。

weak module classifier

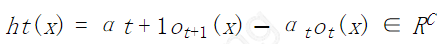
其中 $\alpha$ 为标量，也即 $h$ 是相邻两层 hypothesis 的线性组合。***层没有更低层，因此，可以视为有一个虚拟的低层，$\alpha_0=0$ 并且 $、o_0(x)=0$。

将残差网络显示表示为 ensemble

令残差网络的***输出为 $F(x)$，并接合上述定义，显然有：

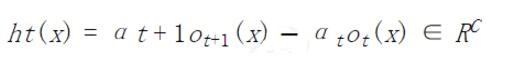
这里用到了裂项求和的技巧（telescoping sum），因此作者称提出的算法为 telescoping sum boosting.

我们只需要逐级（residual block）训练残差网络，效果上便等同于训练了一系列弱分类的 enemble。其中，除了训练残差网络的权值外，还要训练一些辅助的参数——各层的 $\alpha$ 及 $W$（训练完成后即可丢弃）。

2.2 Telescoping Sum Boosting（裂项求和提升）

文章正文以二分类问题为例展开，我们更关心多分类问题，相关算法在附录部分。文章给出的伪代码说明相当清楚，直接复制如下：

其中，$\gamma_t$ 是一个标量；$C_t$ 是一个 m 乘 C （样本数乘类别数）的矩阵，$C_t(i, j)$ 表示其中第 $i$ 行第 $j$ 列的元素。

需要特别说明的是，$st(x, l)$ 表示 $s_t(x)$的第 $l$ 个元素(此处符号用的略随意:-)；而 $st(x) = \sum{\tau=1}^t h\tau(x) = \alpha_t \cdot o_t(x) $。

与算法3中类似，$f(g(x_i), l)$ 表示 $f(g(x_i))$ 的第 $l$ 个元素，$g(x_i, y_i)$ 表示 $g(x_i)$ 的第 $i$ 个元素。

显然 Algorithm 4 给的最小化问题可以用 SGD 优化，也可以数值的方法求解（[1] 4.3 节）。

3. 理论

理论分部没有详细看。大体上，作者证明了 BoostResNet 保留为 boost 算法是优点：1）误差随网络深度（即弱分类器数量）指数减小；2）抗过拟合性，模型复杂度承网络深度线性增长。详细可参见论文。

4. 讨论

BoostResNet ***的特点是逐层训练，这样有一系列好处：

减少内存占用（Memory Efficient），使得训练大型的深层网络成为可能。（目前我们也只能在CIFAR上训练千层的残差网络，过过干瘾）
减少计算量（Computationally Efficient），每一级都只训练一个浅层模型。
因为只需要训练浅层模型，在优化方法上可以有更多的选择（非SGD方法）。
另外，网络层数可以依据训练情况动态的确定。

4.2 一些疑问

文章应该和逐层训练的残差网络（固定或不固定前面各层的权值）进行比较多，而不是仅仅比较所谓的 e2eResNet。
作者这 1.1 节***也提到，训练框架不限于 ResNet，甚至不限于神经网络。不知道用来训练普通深度模型效果会怎样，竞争 layer-wise pretraining 现在已经显得有点过时了。

References

Schapire & Freund. Boosting: Foundations and Algorithms. MIT.
He et al. Deep Residual Learning for Image Recognition.
Veit et al. Residual Networks Behave Like Ensembles of Relatively Shallow Networks.
Xie et al. Aggregated Residual Transformations for Deep Neural Networks.