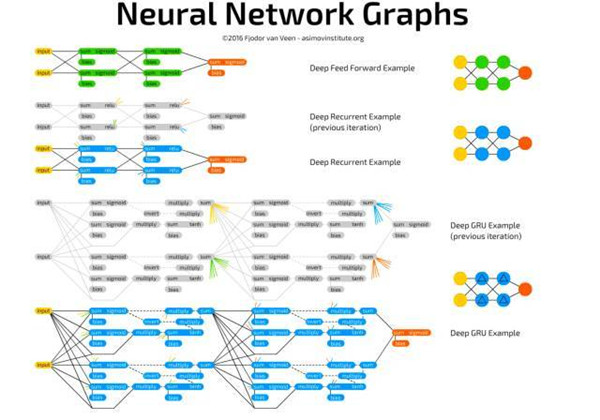
2016 年 9 月,Fjodor Van Veen 写了一篇名为《The Neural Network Zoo》的文章(详见图文并茂的神经网络架构大盘点:从基本原理到衍生关系 ),全面盘点了神经网络的大量框架,并绘制了直观示意图进行说明。近日,他又发表了一篇题为《The Neural Network Zoo Prequel:Cells and Layers》文章,该文是其上篇文章的前篇,对于文中涉及但没有深入展开的神经网络的单元与层的部分再次做了一个图文并茂的介绍。
Cell(单元)
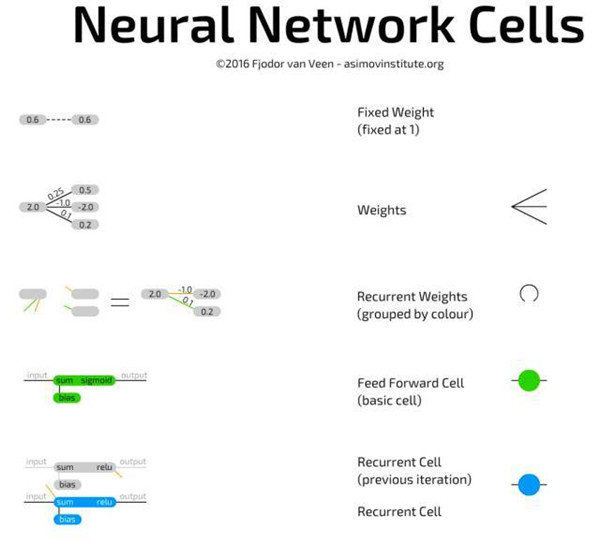
《The Neural Network Zoo》一文展示了不同类型的单元和不同的层连接风格,但并没有深入探讨每个单元类型是如何工作的。大量的单元类型拥有彼此不同的颜色,从而更清晰地区分网络,但是自此之后我发现这些单元的工作方式大同小异,下面我对每个单元逐一描述。
基本的神经网络单元,属于常规性前馈架构之中的类型,且相当简单。单元通过权重与其他神经元相连接,即,它可以连接到前一层的所有神经元。每个连接有其自身的权重,在开始时它常常是一个随机数。一个权重可以是负数、正数、小值、大值或者为 0。它连接的每一个单元值被其各自的连接权重相乘,得到的结果值全部相加。在其顶部,也会相加一个偏置项。偏置项可以防止单元陷入零点输出(outputting zero),加速其操作,并减少解决问题所需的神经元数量。偏置项也是一个数,有时是常数(通常是 -1 或 1),有时是变量。这一总和接着传递至激活函数,得到的结果值即是单元值。
卷积单元和前馈单元很像,除了前者通常连接到前一层的仅仅少数几个神经元之外。它们常用于保护空间信息,因为其连接到的不是少数几个随机单元,而是一定距离内的所有单元。这使得它们很适合处理带有大量局部信息的数据,比如图像和音频(但大部分是图像)。解卷积单元与卷积单元相反:前者倾向于通过局部连接到下一层来解码空间信息。两个单元通常有独自训练的克隆(clone),每个克隆各有其权重,并以相同的方式相互连接。这些克隆可被看做具有相同结构的分离网络。两者本质上和常规单元相同,但是使用不同。
池化和内插单元(interpolating cell)频繁地与卷积单元相连接。这些单元实际上并不是单元,而是原始操作。池化单元接收输入的连接并决定哪些连接获得通过。在图像中,这可被看做是缩小图片。你再也看不到所有的像素,并且它不得不学习哪些像素应该保留哪些舍弃。内插单元执行相反的操作,它们接收一些信息并将其映射到更多的信息。额外信息是组成的,就像放大一个低分辨率图片一样。内插单元不是池化单元***的反转操作,但是二者相对来讲比较普遍,因为其实现快速而简单。它们各自连接,这很像卷积与解卷积。
平均值与标准差单元(几乎完全是作为概率性单元被成对发现)用于表征概率分布。平均值就是平均值,标准差是指在两个方向上能偏离这个平均值有多远。例如,一个用于图像的概率 cell 可以包含一个特定像素上有多少红色的信息。比如说平均值为 0.5,标准差为 0.2。当从这些概率单元中取样时,需要在高斯随机数生成器中输入这些值,值在 0.4 到 0.6 之间的为可能性相当大的结果;那些远离 0.5 的值可能性则很低(但依然有可能)。平均值与标准差 cell 经常全连接到前一层或下一层,并且没有偏差。
循环单元不仅连接到层,并且随着时间推移还会有连接。每个单元内部存储有先前的值。它们就像基本单元一样被更新,但是带有额外的权重:连接到单元的先前值,并且绝大部分时间也连接到同一层的所有单元。当前值和存储的先前值之间的这些权重更像是一个易失性存储器(a volatile memory),就像 RAM,接收拥有一个特定「状态」的属性,同时如果没被馈送则消失。由于先前值被传递到激活函数,并且通过激活函数每一个更新传递这个激活的值连带其他的权重,所以信息将不断丢失。事实上,保留率是如此之低,以至于在 4 至 5 次迭代之后,几乎所有的信息都丢失了。
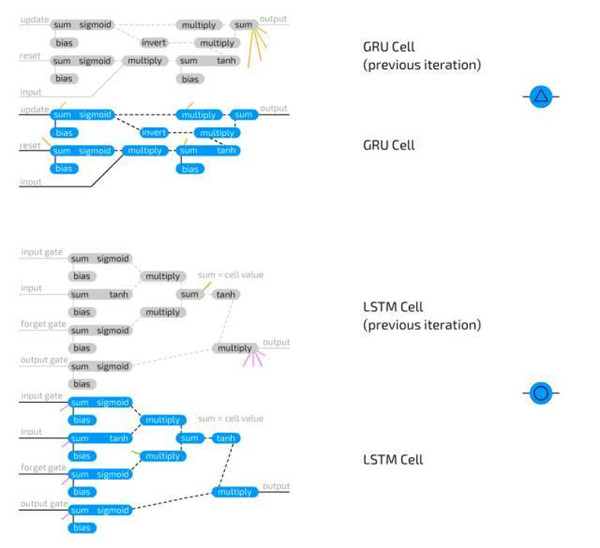
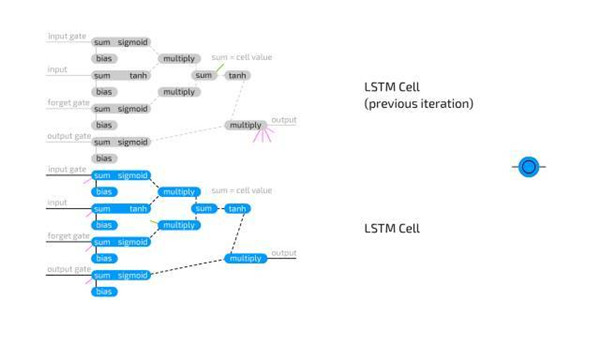
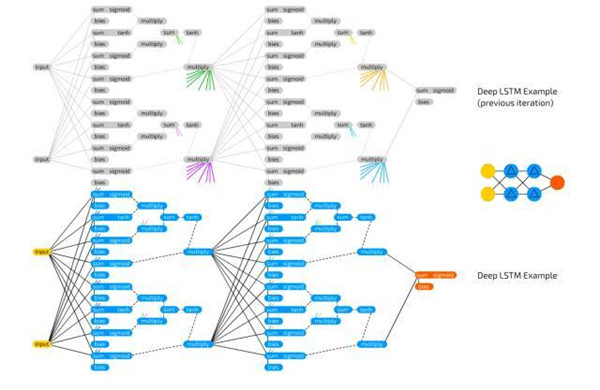
长短期记忆单元用于解决发生在循环单元中信息快速丢失的问题。LSTM 单元是逻辑回路,复制了为电脑设计内存单元的方式。相较于存储两个状态的 RNN 单元,LSTM 单元可存储四个:输出的当前值和最终值,以及「内存单元」状态的当前值和最终值。LSTM 单元包含三个「门」:输入门、输出门、遗忘门,并且也仅包含常规输入。这些门中每一个各有其权重,这意味着连接到这种类型的 cell 需要设置四个权重(而不是仅仅一个)。门函数很像流门(flow gate),而不像栅门(fence gates):它们可以让任何东西通过,只是一点点,没有,或者之间的任何。这通过与值在 0 到 1(储存在这一门值中)之间的输入信息相乘而发挥作用。输入门接着决定有多少输入可被加入到单元值中。输出门决定有多少输出值可通过剩余的网络被看到。遗忘门并不与输出单元的先前值相连接,但却与先前的内存单元值相连接。它决定了保留多少最终的内存单元状态。由于它不连接到输出,所以信息丢失更少,因为循环中没有放置激活函数。
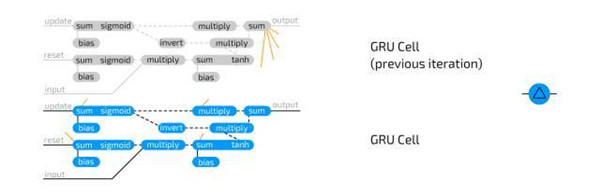
Gated 循环单元是 LSTM 的一种变体。它们也是用门防止信息丢失,但也就两种门:更新门(update) 和重置门(reset)。这略微缺乏表现力,但更快。因为它们在处处都有更少的连接。其实,LSTM 和 GRU 之间有两个不同:GRU 没有输出门保护的隐单元态,而是把输入和遗忘门结合成了一个更新门。其中的思路是,如果你想要大量的新信息,可以遗忘一些旧信息(或者相反)。
层
将神经元连接成图的最基础方式是将一切相互连接,这可以在 Hopfield 网络和玻尔兹曼机中看到。当然,这意味着连接的数量会有指数级的增长,但表现力是不折不扣的。这被称为全连接。
而后,有人发现将网络分成不同的层是有用的,其中一层的一系列或一组神经元之间不连接,但与其他组的神经元相连接。例如受限玻尔兹曼机中的网络层。如今,使用层的观念已经推广到了任何数量的层,在几乎所有的架构中都能看到。这也被称为全连接(可能有点混淆),因为实际上完全连接的网络很不常见。
卷积连接层要比全连接层更受限制:每个神经元只与其他组相近的神经元连接。图像和音频包含大量的信息,不能一对一地被用于直接馈送到网络(例如,一个神经元对应一个像素)。卷积连接的思路来自于对保留重要的空间信息的观察。结果证明,这是一个好的想法,被用于许多基于神经网络的图像和语音应用中。但这种设置没有全连接层更具表达力。其实它是一种「重要性」过滤的方式,决定这些紧凑的信息数据包中哪些是重要的。卷积连接对降维也很棒。依靠其实现,及时空间上非常远的神经元也能连接,但量程高于 4 或 5 的神经元就很少被用到了。注意,这里的「空间」通常指代二维空间,用这种二维空间表达神经元互相连接的三维面。连接范围在所有的维度都能被应用。
另一个选择当然就是随机连接神经元了(randomly connected neurons)。它也有两个主要变体:允许一部分所有可能的连接,或者连接层之间神经元的一部分。随机连接有利于线性地减少网络的表现,可被用于陷入表现问题的大型网络的全连接层。在某些情况下,有更多神经元的更稀疏的连接层表现更好,特别是当有大量的信息需要存储,但不需要交换时(有点类似于卷积连接层的效力,但却是随机的)。就像 ELM、ESN 和 LSM 中看到的,非常稀疏的连接系统(1% 或 2%)也会被用到。特别是在脉冲网络(spiking network)中,因为一个神经元有越多的连接,每个权重携带的能量越少,意味着越少的传播和模式重复。
延时连接是指神经元间并非从前面的层获得信息,而是从过去获得信息(大部分是之前的迭代)。这使得时间信息(时间、时序)可被存储。这类连接有时要手动重置,从而清除网络的「state」。与常规连接的主要不同是这些连接持续在变化,甚至在网络没被训练时。
下图展示了以上描述内容的一些小样本网络及其连接。在不知道什么连接什么时,我就会使用它(特别是在做 LSTM 或 GRU cell 时):