对人类而言,转写是一件相对容易并且可解释的任务,所以它比较适合用来解释神经网络做了哪些事情,以及神经网络所做的事情是否和人类在同样的任务上做的事情有相似之处。因此,我们从转写任务开始进一步从可视化的角度解释神经网络中的单个神经元实际上都学到了什么,以及它们到底是如何决策的。
目录:
- 转写
- 网络结构
- 分析神经元
- 「t」是如何变成「ծ」的?
- 神经元 是如何学习的?
- 可视化长短期记忆(LSTM)网络中的单元(cell)
- 总结评论
转写(Transliteration)
数十亿互联网用户中,大约有一半在使用非拉丁文字母(non-Latin alphabets)表示的语言,例如俄语、阿拉伯语、中文、希腊语以及亚美尼亚语等。很多时候他们也会随意地用拉丁文字母来写这些语言。
- Привет: Privet, Privyet, Priwjet, …
- كيف حالك: kayf halk, keyf 7alek, …
- Բարև Ձեզ: Barev Dzez, Barew Dzez, …
因此,用户生成的内容中使用「拉丁化」或者「罗马化」的格式内容越来越多,这些格式的内容难以解析、搜索,甚至识别。转写就是就是将这些内容自动地转换成规范格式的任务。
- Aydpes aveli sirun e.: Այդպես ավելի սիրուն է:
什么因素使得这个问题比较困难呢?
- 如上所示,不同的语言使用者会用到不同的罗马化方式。例如,v 或者 w 在亚美尼亚语中被写为վ。
- 多个字母可以被罗马化成一个拉丁字母。例如 r 可以代表亚美尼亚语中的 ր 或者 ռ。
- 一个单个字母可以被罗马化成多个拉丁字母或者拉丁字母的组合。例如,ch 组合代表西里尔字母中的ч或者亚美尼亚子母中的 չ,但是 c 和 h 各自又代表其他的东西。
- 英语单词和跨语言的拉丁文标志,例如 URL,通常都以非拉丁文本的形式出现。例如,youtube.com 和 MSFT 中的字母不会被改变。
人类很擅长解决这些模棱两可的东西。我们曾经展示过 LSTM 也能够学会解决所有的这些歧义性,至少在亚美尼亚语上。例如,我们的模型可以正确地将 es sirum em Deep Learning 转写为ես սիրում եմ Deep Learning,而不是ես սիրում եմ Դեեփ Լէարնինգ。
网络架构
我们从维基百科上取了很多亚美尼亚文本,并使用概率规则(probabilistic rules)来得到罗马化的文本。概率规则覆盖了人们在亚美尼亚语中使用的大多数罗马化规则。
我们把拉丁字母编码成了 one-hot 向量,然后使用字符级别的双向 LSTM。在每一个时间步长上,网络都会尽力去猜测原始亚美尼亚语句子中的下一个字符。有时候一个单独的亚美尼亚字母会由多个拉丁文字母表示,所以在使用 LSTM 之前将罗马化的文本和原始文本对齐是很有帮助的(否则,我们需要使用句子到句子的 LSTM,但是这种网络非常难以训)。幸好我们可以对齐,因为罗马尼亚文本只由我们自己生成的。例如,dzi 应该被转写成ձի,其中 dz 与ձ对应,i 与ի对应。因此我们在亚美尼亚文本中添加了一个占位符:ձի 变成了 ձ_ի,因此现在 z 可以被转写为 _。在转写完成之后我们只需要将输出字符串中的所有 _ 清除掉即可。
我们的神经网络包含两个 LSTM(共有个 228 个单元),它会沿着拉丁文序列向前和向后遍览。LSTM 的输出在每个步骤都是相连的(连接层),然后一个具有 228 个神经元的紧密层(dense layer)用在隐藏层的顶部,然后再用一个使用 softmax 激活函数的紧密层(输出层)来得到输出概率。我们还将输入层与隐藏层连在一起,这样就有 300 个神经元了。这比我们之前的博客中描述的相同主题上使用的简化版网络更加简洁(主要的区别就是我们没有使用双向 LSTM(biLSTM)的第二层)。
分析神经元
我们尝试回答下面的两个问题:
- 网络如何处理具有几个可能的输出结果的例子?(例如 r => ր vs ռ 等等)
- 特定的神经元都解决了什么问题?
「t」是如何变成「ծ」的?
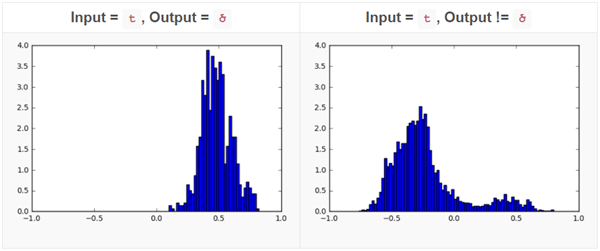
首先,我们使用一个特定的字符作为输入,另一个特定的字符作为输出。例如,我们对「t」是如何变成「ծ」比较感兴趣(我们知道 t 可以变成 տ、թ 或者ծ)。
我们对每一个神经元的正确输出是ծ和不是ծ的情况都绘制了直方图。对大多数神经元来说,这个直方图都是比较相似的,只是有以下这两种情况而已:
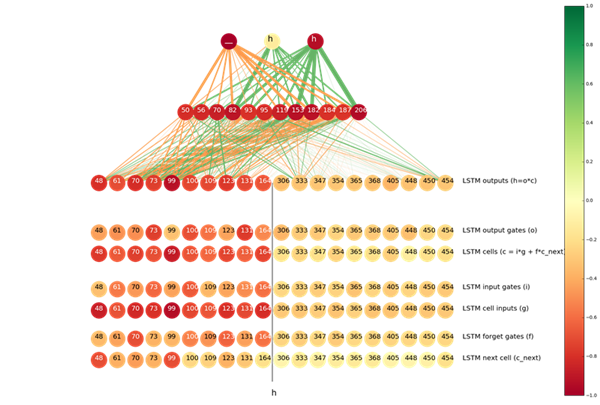
这两幅直方图表明,通过观察这个特定神经元的激活结果,我们就能够以较高的准确率猜到 t 的输出结果是不是ծ。为了量化这两幅直方图的差别,我们使用了海宁格距离(Hellinger distance),即我们得到对神经元激活结果的***值和最小值,并将它们之间划分成 1000 分,然后应用海宁哥距离公式。我们计算了每一个神经元的海宁格距离,然后将最感兴趣的那些以一幅图展示了出来:
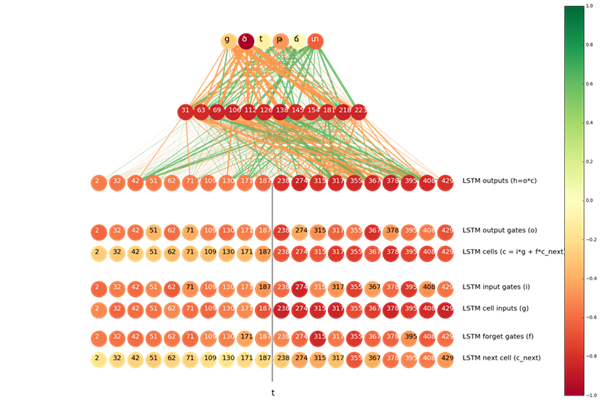
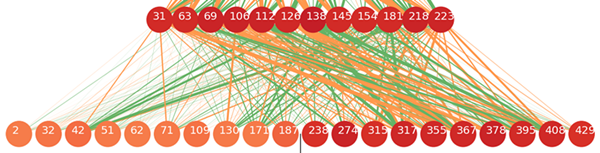
神经元的颜色代表两幅直方图之间的距离(更深的颜色意味着更大的距离)。两个神经元之间连线的线宽代表从更低层到更高层的连接贡献,即均值。橙色和绿色的线分别代表正或负的信号。
图片顶部的神经元来自于输出层,输出层下面的神经元来自于隐藏层(顶部的 12 个神经元表示直方图之间的距离)。隐藏层下面是连接层。连接层的神经元被分成两部分:左半部分神经元是从输入序列向输出序列传播的 LSTM,右半部分是从输出向输入传播的 LSTM。我们根据直方图的距离从每个 LSTM 中展示出了前十个神经元。
在 t => ծ 的情况中,很明显隐藏层的前 12 个神经元都向 ծ 和ց(ց 在亚美尼亚语言也经常被罗马化成 t)传递正信号,向 տ, թ 以及其他的字符传递负信号。
我们也可以发现从右到左的输出颜色更加深,这表明这些神经元「拥有更多关于是否要预测成ծ的知识」,另一方面,这些神经元和隐藏层之间的连线颜色却更加浅,这意味着他们对隐藏层中顶部的 12 个神经元激活程度的贡献更大。这是非常自然的结果,因为当下一个符号是 s 的情况下,t 一般会变为ծ,而且,仅仅从右向左的 LSTM 才能意识到下一个字符。
我们对 LSTM 内部的神经元和门(gate)做一下类似的分析。分析结果在图中底部的 6 行展示了出来。实际上,有趣的是最「置信的」神经元是那些所谓的单元输入(cell input)。输入单元和门都依赖于当前步骤的输入和前一步的隐藏状态(就像我们谈论过的从右向左的 LSTM,这是下一个字符的隐藏状态),因此它们都「意识」到了下一个 s,但是因为一些原因,单元输入比其他部分更具置信度。
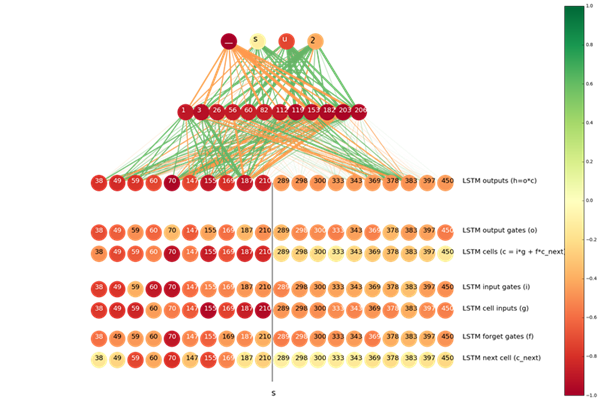
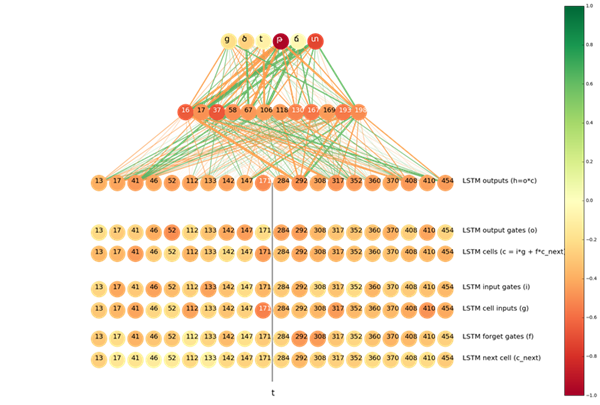
在 s 应该被转写成_(占位符)的情况下,随着 s 变成 _ ,尤其是在 ts => ծ_的情况下,有用的信息更可能来自输入到输出的正向 LSTM。在下图中可以看到这个情况:
神经元是如何学习的?
在分析的第二部分我们阐释了在有歧义的情况中,每个神经元是如何起到帮助作用的。我们使用了可以被转写为不止一种亚美尼亚字母的拉丁字符集。然后我们移除了在 5000 个样本句子中出现次数少于 300 次的样本结果,因为我们的距离因子(distance metric)在那些更少的样本上不太奏效。然后我们在给定输入-输出对的情况下分析了每一个神经元。
例如,这是对从左到右的 LSTM 中输出层编号为 #70 的神经元的分析。我们在之前的可视化中看到,它有助于决定 s 是否会被转写为_。下面是这个神经元判断的排名前 4 的输入-输出对:
所以这个神经元最有助于将 s 预测为_(这个我们早就知道了),但是它也有助于决定拉丁字母 h 是否要被转写为亚美尼亚字母հ或者占位符_(例如,亚美尼亚字母չ通常被罗马化为 ch,因此 h 有时候会变成_)。
当输入是 h,输出是_的时候,我们可视化了神经元激活程度直方图之间的海宁格距离(Hellinger distances),结果发现,在 h=>_的情况下,编号为 #70 的神经元也属于从左到右的 LSTM 中顶部十个神经元的一个。
可视化 LSTM 单元
受到论文可视化和理解循环网络(Visualizing and Understanding Recurrent Networks,Andrej Karpathy、Justin Johnson 和 Fei-Fei Li)的启发,我们尝试寻找对后缀թյուն(罗马化为 tyun)反应***烈神经元。
***行是输出序列的可视化。下面几行展示了最有趣的神经元的激活程度:
- 输出到输入反向 LSTM 中编号为 #6 的单元
- 从输入到输出正向 LSTM 中编号为 #147 的单元
- 隐藏层中的第 37 个神经元
- 连接层中的第 78 个神经元
我们可以看到,单元 #6 在 tyuns 上表现的很活跃,但是在序列中的其他部分则并不活跃。前向 LSTM 中的单元 #144 则有完全相反的表现,它对除了 tyuns 之外的一切都感兴趣。
我们知道,在亚美尼亚语种,tyuns 中的前缀 t 总应该变成թ,因此我们认为,如果一个神经元对 tyuns 感兴趣,那么它有可能会有助于决定拉丁文 t 是否应该别转写为 թ 或者 տ。所以我们可视化了在输入输出对 t => թ的情况下最重要的神经元。
事实上,前向 LSTM 中的单元 #147 也是属于 top 10 的。
结语
神经网络的可解释性仍然是机器学习中的一个挑战。卷积神经网络和长短期记忆对很多学习任务都表现良好,但是鲜有工具能够理解这些系统的内部运作机制。转写是一个用来分析实际神经元作用的很好的问题。
我们的实验证明,即使在很简单的例子中,也会有大量的神经元参与决策,但是能够找到那些比其他神经元更具有作用的一个神经元子集。另一方面,根据上下文,大多数神经元都涉及到了多个决策过程。由于我们在训练神经网络时所用的损失函数并没有强制让神经元之间相互独立并且可解释,所以这是意料之中的。最近,为了得到更多的可解释性,已经有人尝试使用信息理论的正则化方法。在转写的任务中测试这些思想将会很有趣。