这篇文章主要回答量化问题。量化问题主要包括以下情况:
“据我所知,每个方向0的衍生机率很低。除此之外,还有其他原因吗?”
理论上,这个问题是可以验证的,而且这几十年间也有很多研究人员一直在致力于验证它。
首先,我想指出无论如何这个问题已在实践中得到了验证。这个观点最初由LeCun在他早期的著作中提出。现在David G. Stork, Peter E. Hart, 和 Richard O. Duda合著的“小红书”《图形分类》中有讨论。
20年前旋转玻璃研究中这个问题已在浓缩物质物理学中被大量解释。
最基础的项目由Parisi通过一个类似的非现实形式开发研究:
以静态的观点表现TAP的自由能量
后来采用了无规矩阵理论实证的正确可行的方法论证。LeCun所谈及的结果如下:
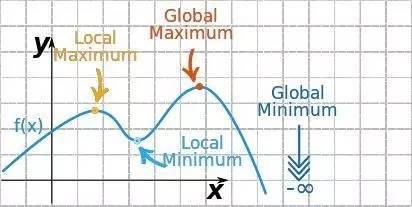
高维景观的关键点
我来总结一下Parisi的方法:
他研究随机哈密尔敦函数的其中一种——平均场自旋玻璃,被称作P状旋转的球状旋转玻璃。他发现:
1.得出TAP自由能量的分析表达式(当T>0时)TAP(索利斯安德森帕尔默)理论是研究旋转玻璃的一般方法,而且能应用于RBMs(可参阅《使用物理化学提高RMBs》)
2.可计算构形的平均信息量,除此之外,还有复杂性度量——通过统计学理论的方法计算关键点的数量。
3.为了在能量水平E时计算关键点数量,可延伸这一结论到T=0的能量景观。Paris得出的普适结果是所有本地最小化能量“集中(静态上)”在轻微高于地球表面的一小部分地带中。
一直未解释的是为什么在研究旋转玻璃中这是一个重要问题以及为什么P形球状旋转玻璃是研究目标,除了它是一个已被论证的模型以及有大量深度学习研究人员可得出的硬性设想。
此外,在深度学习研究中,T=0能量观景与T>0能量观景之间没有区别,虽然在传统的方法中如RBMs和VAEs是假设T=1。
最近有更多的结论可尝试直接应用于深度学习研究中:
不存在极少的局部最小值的深度学习
这一结论进一步假设SGD解决者实际中无法分辨鞍点与局部最小值的区别,因为Hessian理论的假设是很有问题的。LeCun最近的数值计算研究证实了这一点。他的研究显示Hessian理论假设有很多0值。
偏向性梯度下降至谷底
我个人认为这一结论还不完整,而且对于物理化学家,例如沃利尼斯*彼特来说,这方面的问题还有大量研究工作。这个议题在被称作“亚当的肋骨”现象以及关联的在真实结构性玻璃出现的平均信息量危机的极冷玻璃理论中一个让人非常迷惑的现象。这个题目很深奥,但足以说明P旋转球状旋转玻璃非常有趣的原因是这是一个简单的旋转玻璃模型,具有大量的真实能量观景。它表现了平均信息量危机。事实上,我设想深网也将表现出平均信息量危机,例如:当深网被过度训练后他们会呈现出很多假设性的平均信息量。
由于过度训练而引发的平均信息量危机将呈现为高耸的山峰,因为它已偏离假设性平均信息量,类似于LeCun在他的关于平均信息量SGD论著中提及的。而且这一现象最近在RBMs被观察到。
[1612.01.1717] 具有二元突触的限制性波尔兹曼机器的非监控特征的统计力学
这些漏斗状的观景可从蛋白质折叠中观察到。
那么,为什么深度学习可行呢?
我在UC 伯克利大学的2016夏季MDDS 讨论中谈及了这些问题 (可点击 阅读原文 查看视频)。


































