下面主要写了数据结构课本上介绍的「十种排序算法」,趁着快考试了复习一波排序,有图有真相,看不懂打死我吧。
堆排序、快速排序、希尔排序、直接选择排序不是稳定的排序算法,而基数排序、冒泡排序、直接插入排序、折半插入排序、链表插入排序、归并排序是稳定的排序算法。
直接插入排序 T(n) = O(n^2)
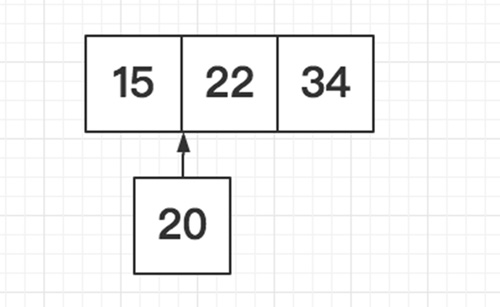
直接插入排序「Insertion Sort」的基本思想是:每次将一个待排序的记录,按其关键字大小插入到前面已经排好序的子序列中的适当位置,直到全部记录插入完成为止。
设数组为a[0…n-1]:
- 初始时,a[0]自成1个有序区,无序区为a[1..n-1]。令i=1。
- 将a[i]并入当前的有序区a[0…i-1]中形成a[0…i]的有序区间。
- i++并重复第二步直到i==n-1。排序完成。
折半插入排序 T(n) = O(n^2)
折半插入排序是对直接插入排序的简单改进,对于折半插入排序而言,当需要插入第i个元素时,它不会逐个进行比较每个元素,而是:
- 计算0~i-1索引的中间点,也就是用i索引处的元素和(0+i-1)/2索引处的元素进行比较,如果i索引处的元素值大,就直接在(0+i-1)/2~i-1半个范围内进行搜索;反之在0~(0+i-1)/2半个范围内搜索,这就是所谓的折半
- 在半个范围内搜索时,按照1的方法不断地进行折半搜索,这样就可以将搜索范围缩小到1/2、1/4、1/8…,从而快速的确定插入位置
链表插入排序 T(n) = O(n^2)
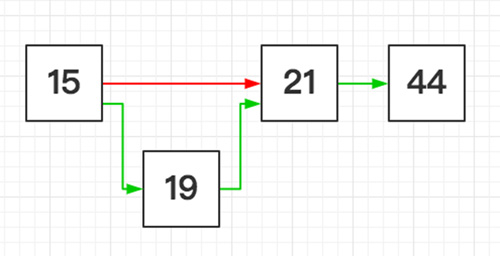
链表插入排序的基本思想是:假设前 n-1个节点有序,取***节点,沿链表依次查找比较,直到合适位置,修改「本节点」和「待插入节点」的指针。
- 沿头节点遍历链表,比较此节点、待插入节点、后继节点的大小关系,直到:此节点 < 待插入节点 < 后继节点。
- 令「此节点」指向「待插入节点」,「待插入节点」指向「后继节点」。
Shell 排序(希尔排序) T(n) = O(n^1.5)
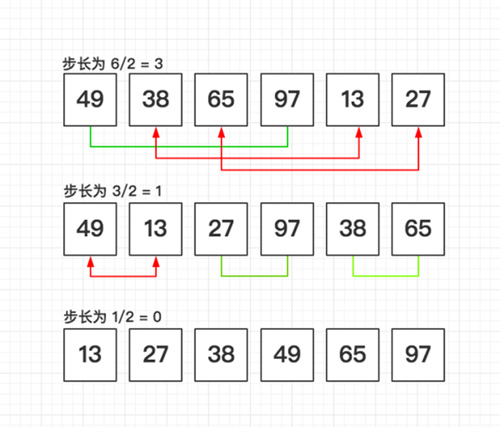
希尔排序的实质就是分组插入排序,该方法又称缩小增量排序。该方法的基本思想是:
- 先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序
- 然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小,1)时,再对全体元素进行一次直接插入排序
冒泡排序 T(n) = O(n^2)
冒泡排序的基本思想是,对相邻的元素进行两两比较,顺序相反则进行交换,这样,每一趟会将最小或***的元素“浮”到顶端,最终达到完全有序。
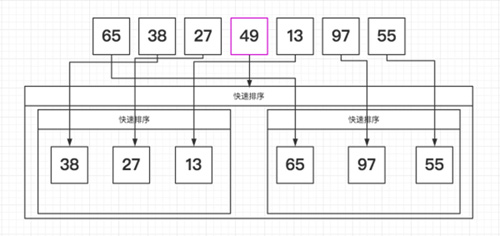
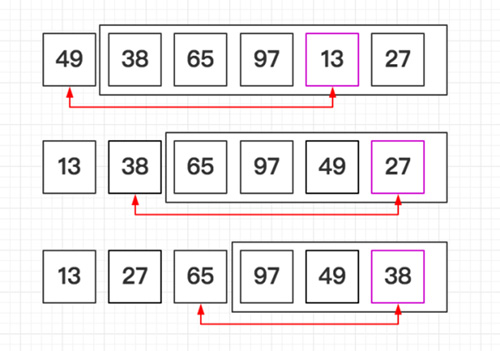
快速排序 范围T(n) = O(n*lg n) ~ O(n^2) | 平均T(n) = O(n*lg n)
快速排序采用了分治(递归)的方法,该方法的基本思想是:
先从数列中取出一个数作为基准数
分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边
再对左右区间重复第二步,直到各区间只有一个数
直接选择排序 T(n) = O(n^2)
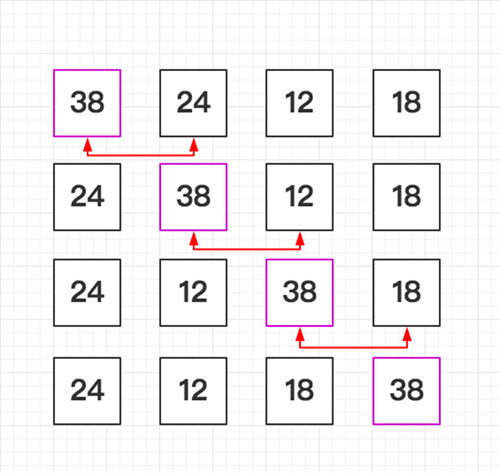
直接选择排序(Straight Select Sorting) 也是一种简单的排序方法,它的基本思想是:
- 从R[0]~R[n-1]中选取最小值,与R[0]交换
- 从R{1}~R[n-1]中选取最小值,与R[1]交换
- 第i次从R[i-1]~R[n-1]中选取最小值,与R[i-1]交换
堆选择排序 T(n) = O(n*log2n)
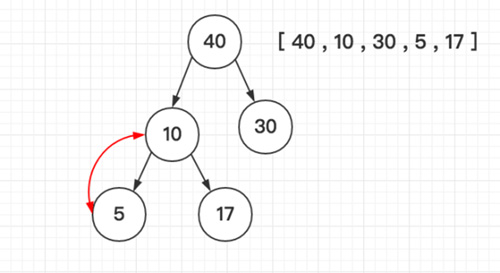
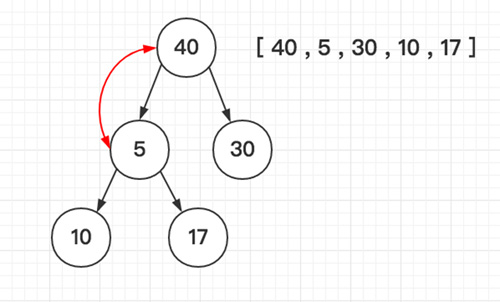
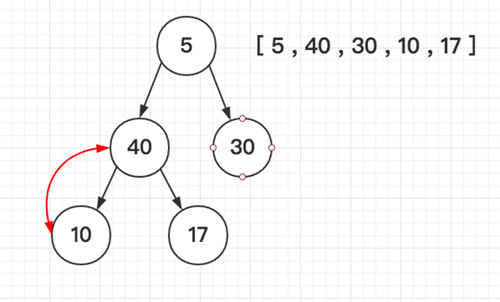
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。堆分为大根堆和小根堆,下图为小根堆:
「如图所示依次类推」
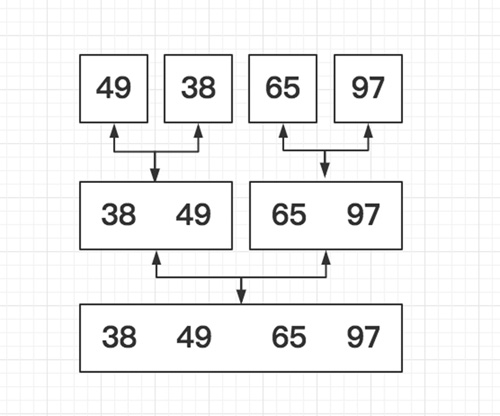
归并排序 T(n) = O(n*log2n)
归并排序是建立在归并操作上的一种有效的排序算法,采用了分治思想。如下图的二路归并:
基数排序
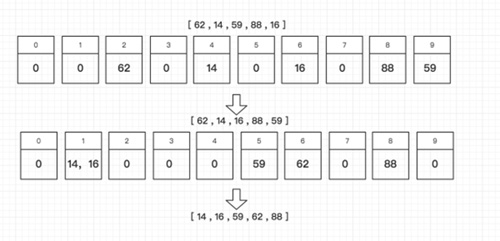
基数排序(radix sort)属于「分配式排序」,有点类似 「桶排」。
- 分配10个桶,桶编号为0-9,以个位数数字为桶编号依次入桶,将桶里的数字顺序取出来
- 再次入桶,不过这次以十位数的数字为准,进入相应的桶,同一桶内有序
- 再次取出,排序完成