本文是一篇很好的综述论文:结果很容易理解,也让人有些惊讶,但其意指又会让人思考良久。
对于文中的问题,作者是这样回答的:
如何区分泛化能力好的与差的神经网络?问题答案是泛化能力好的神经网络不仅有助于提升网络解释性,而且还可以带来更有规律、更可靠的模型架构设计。
所谓的「泛化能力好」,作者对此做出的简单解释是「那些在训练集上表现好的网络在测试集上也有良好的表现?」(与迁移学习不同的是,这涉及将训练过的网络应用于相关而又不相同的问题中)。如果你思考一下,这个问题几乎归结为为什么神经网络可以跟它们工作的一样好?泛化性与仅仅记忆部分训练数据并将其重新编写返回不同,泛化性实际上是开发了一些可用于预测数据的有意义的能力。所以这可能会让人有一点懊恼,如果这个问题「为什么神经网络的可以跟其他模型工作的一样好」的答案是「我们真的不知道」,那么也就不会有懊恼了。
随机标签的奇怪案例
我们的故事从熟悉的地方开始---CIFAR 10(50000 张训练图像,分为 10 类,另有 10000 张验证图像)、2012 年的 ILSVR(1281167 张训练图像,50000 张验证图片,并且有 1000 个类) 的数据以及 Inception 网络架构的变体。
用训练数据训练网络,在训练集上达到零误差你肯定不会感到奇怪。这是一个很明显的过拟合训练示例,而不是学习真实的预测特征。我们采用诸如正则化技术防止过拟合,而且能使模型获得更好的泛化能力,关于正则化后文会有细述。
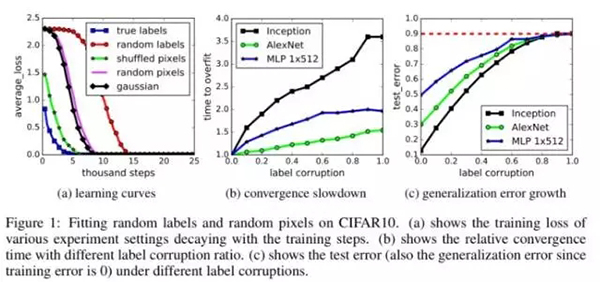
采用相同的训练数据,但这次使用随机的标签 (即这样使得标签和图像中的内容之间不再有真正的对应关系)。用这些随机的标签训练网络然后你会得到什么?零训练误差!
在这个例子中,实例和类别标签之间没有任何的关系。因此,学习是不可能的。这直观地表明了这种不可能性在训练过程中应该自我表现的很清楚,例如在训练之后误差是不可能收敛或者减小的。令我们惊讶的是,多标准架构的训练过程中的几个属性很大程度上不受这个标签转换的影响。
正如作者总结所言,「深度神经网络很容易拟合这些随机标签」。这是***个实验中获得三个重要发现:
- 神经网络的有效容量足够记忆整个数据集。
- 尽管优化随机标签依旧容易,实际上与使用真正标签的训练比,随机标签训练的时间只多了一个小的常数时间。
- 随机标签只不过是一个数据转换,而学习问题的所有其他属性不变。
如果你用随机标签训练网络,然后看网络在测试集中的表现,这个表现显然不好,这是因为网络没有学习到数据集的正确信息。这一问题的一个奇怪描述是它具有高泛化误差。将这些情况综合考虑,你能理解到:
- 单独通过随机标签,在不改变模型的大小、超参数或者优化下,我们可以强制明显地提高模型的泛化误差。我们在 CIFA 10 和 ImageNet 分类基准上训练的几种不同标准体系确立了这个事实。
- 或易言之,模型及其大小、超参数和优化器并不能解释当前***进神经网络的泛化能力。这正是由于模型可以毫无变化,但是泛化能力的表现可以千差万别。
更奇怪的随机图像案例
如果我们不仅仅是弄乱标签,而且弄乱图像本身会发生什么?事实上,如果用随机噪声替换真实图像又会怎么样?在图中,这个被称为「高斯」实验,因为是使用与原始图像相匹配的均值和方差的高斯分布生成每张图像的随机像素。
事实证明,网络依然能够训练到零误差,但是速度比随机标签更快。至于为什么会发生这种情况的假设是:随机像素比随机化标签的原始图像更容易区分,这是因为原始图像中属于同一个类别的图像在经过类别随机化后被学习为其他类别。
带有一系列变化的团队实验将不同程度和种类的随机化引入数据集:
- 真实标签(没有经过任何修改的原始数据集)
- 部分坏标签(弄乱部分标签)
- 随机标签(弄乱所有标签)
- 混合像素(选择一排像素,然后将它应用于所有图像)
- 随机像素(对每个图像使用不同的排列)
- 高斯(仅是为每张图片填充,如前所述)
所有的这一系列方法,网络依旧可以很好的拟合这些训练数据。
此外,我们进一步改变随机化的数量,在无噪声和全噪声的情况下平滑内插。这会导致一系列中间学习的问题,其中标签中存在一定的信号。随着噪声的不断加大,我们发现泛化误差也不断的加大。这说明神经网络能够捕获数据中的剩余信号,同时使用蛮力来拟合部分噪声。
对我来说***一句是关键。我们在模型中做出的某些选择清楚的表明了模型泛化能力的差异(否则所有的架构应该具有相同的泛化能力)。在数据中没有其他真实信号时,世界上泛化能力***的网络依旧需要回顾一下。所以我们可能需要一种方法去挑选数据集中存在的真正泛化能力,以及给定模型架构在捕捉这种潜力的效率。一个简单方法是用不同架构的模型训练在同样的数据上训练(当然我们一直是这样做的)。这依然不能帮助我们解决原始问题,但是可以理解为什么一些模型的泛化能力比其他模型好。
用正则化弥补?
模型架构本身显然不能充分正规化(不能防止过拟合/记忆),但是常用的正则化技术呢?
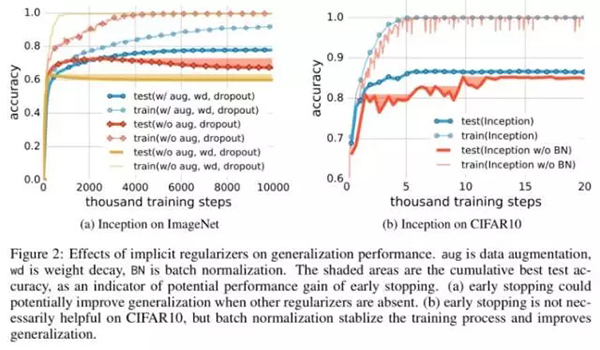
如下我们显示采用一些正则化技术,例如权重衰减 、dropout、增加一些数据都足以解释神经网络的泛化误差:采用正则化可能会提供模型的泛化能力,但这并不是必须的也不足以控制泛化误差。
显性正则化似乎更多的是一个调整参数,有助于提高泛化能力,但是其缺失也并不意味着泛化误差。当然并非所有能够拟合训练数据的模型都能很好地泛化。本文分析中的有趣一面是,我们仅仅通过使用梯度下降过程就获得了一定量的正则化:
我们分析 SGD 如何作为一个隐性正则器。对于线性模型,SGD 经常收敛到一个小规模的解决方案。因此算法本身隐性地正则化了解决方案,尽管这个无法解释为什么某些架构比其他架构泛化能力更好,但却表明需要使用更多的研究来了解 SGD 的内在属性。
机器学习模型的有效容量
考虑样本大小为 n 的神经网络情况,如果网络有一个参数 p,p 比 n 更大,然后尽管一个简单的两层神经网络可以表示输入样本的任何函数。作者证明(在附录中)以下定律:
存在一个带有 ReLU 激活函数、有 2n+d 个权重的二层神经网络,可以表示大小为 n*d 的样本上的任何函数。
所以这一切都偏离我们了?
这种情况对统计学习提出了一个概念上的挑战,因为传统的模型复杂度度量很难解释大型人工神经网络的泛化能力。我们的任务在这个巨大的模型下,且还没有发现简单准确的度量方法。从我们的实验得出的另一个解释是:即使是模型的泛化能力不好,通过经验优化模型也是比较容易的。这表明了优化为什么容易的经验性原因,肯定不同于真正的泛化原因。
【本文是51CTO专栏机构机器之心的原创译文,微信公众号“机器之心( id: almosthuman2014)”】