罗马12毫米骰子,PAS(一个英国政府管理下的保护文物志愿者组织)/大英博物馆董事(CC BY-SA 2.0)
统计学家弗朗西斯 · 加尔顿于1890 年《自然》杂志上写道:“作为一个选择随机的工具,我发现没有什么优于骰子。把它们扔进装骰子的盒子中摇动,它们彼此相互冲撞,并与盒壁碰弹,不停的滚动,即使在一次摇骰子中,骰子的最初朝向也无法为其最终的朝向提供任何有用的线索。”
我们如何才能生成一个均匀的随机数序列?大自然中产生的如此美丽和丰富的随机性并不总可以被轻松的提取和量化。最古老的骰子是在公元前24世纪中东的一个坟墓中被发现的。大约在公元前1100年,在中国,龟卜中火热龟壳直到其随机破裂,然后占卜者对龟壳裂缝进行解释。几个世纪之后,易经卜卦中将49条蓍草茎放在桌子上,按一定规则切分几次,其结果类似于执行硬币投掷。
摘自《A Million Random Digits with 100,000 Normal Deviates》
但是到了二十世纪40年代中期,现代世界需要更多的随机数,远超过骰子和蓍草茎可提供的范围。兰德公司研发了一种机器可以使用随机脉冲发生器产生随机数。他们运行了一段时间,并收集到一本书中《A Million Random Digits with 100,000 Normal Deviates》。现在看来,这似乎是一个好笑的艺术项目,但在当时却是一大突破,这是第一次为公众提供了一个高质量的长随机数序列。兰德公司在2001重印了该书,现在在亚马逊上可以购买。
另外还有一个类似的机器:摇奖机,是有当时著名的Bletchley Park WWII 破译小组于上世纪40年代设计的,用来为英国的保险债券彩票产生随机数。为了减轻对ERNIE公正性和准确性的担忧,公司做了一个伟大的纪录片,称为“E.R.N.I.E.的重要性”,非常值得一看:The Importance of Being E.R.N.I.E. 。
1951年,随机数生成终于被正式地内嵌到一台真正的计算机中:Ferranti Mark 1 ,它带有一个内置的随机数指令,可以使用电气噪声一次生产20个随机比特。这个功能由阿兰·图灵设计,Christopher Strachey 通过利用它编写一个随机的情书发生器。下面是一个情书的例子,来自David Link该项目的2009 复合计划。
| 亲爱的,
我对你的可爱迷恋至极。 你勾起了我所有对情爱的幻想。 我为你而狂热。 你的魅力使我对你充满了渴望。 我的心随你在而让我无法呼吸。 你的追求者 M.U.C |
但是图灵的随机数字指令让当时的程序员感到非常困惑,因为它在一个已经如此不可预测的环境中造成了太多的不确定性。人们期望软件的一致性,但使用该指令的程序永远无法以一种一致性的可重复方式运行,这使得测试几乎不可能。
如果一个随机数发生器可以表示为确定性函数呢?如果可以重复调用一个随机数序列,但在相同的初始化条件下,它总是会产生相同的序列呢?这就是伪随机数发生器(PRNG)。
冯·诺依曼在1946年左右开发了一个PRNG,他的想法是从一个初始的随机种子值开始对其平方,然后截取平方结果的中间若干位,得到一个新的数字,接下来重复对得到的数取平方并截取中间若干位的过程,就会得到一个具有统计意义属性的随机数序列了,这也就是广为人知的平方取中法。
冯·诺依曼的方法没有经受住时间的考验,因为无论使用什么样的种子值,序列最终会陷入一系列短重复周期的数字,如8100,6100,4100,8100,6100,4100……
当使用确定性函数生成随机数序列时,如果后续值基于先前值,避免循环是不可能的。但是如果周期足够长,使之对随机序列实际上影响不大呢?
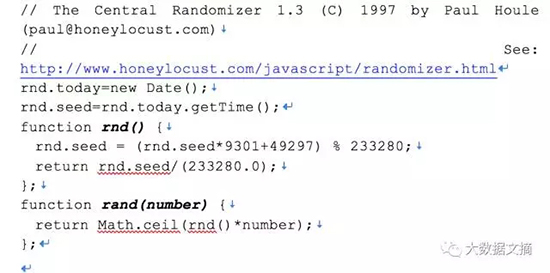
依照这一想法,数学家D.H.Lehmer在1949年提出了线性同余生成器(LCG)。这里介绍一个简单的PRNG,叫做中央随机数生成器,便是基于Lehmer的方法,于1995年采用JavaScript编写实现如下:
注意这里的所有幻数,选择这些数字(通常是素数)用来最大化周期:在rand()生成序列之前迭代次数将自我重复。该PRNG使用当前时间作为种子值,其周期值约为2的31次方。
中央随机生成器指针变得流行是因为JavaScript 1.0没有内置的Math.random()函数,每个人都希望他们的Web 1.0横幅广告随机旋转。开发者Paul Houle写道:“我不会用它来保密,但它对许多用途都是有好处的。”
然而互联网确实需要保密。 SSL诞生于1995年左右,其加密方案要求高质量的PRNG,这种发展可能导致了一段RNGs 迅猛创新的时期。如果查看所有的随机数生成器的专利,可能会感觉就像现代版的第一次制造飞机的浪潮一样。
20世纪90年代中期最常见的CPU没有生产随机数的指令,所以好的随机种子很难在当时得到。当Phillip Hallam-Baker发现Netscape的SSL网络服务器(当时市场上最大的一个)使用当前时间和几个进程ID的组合作为其随机数生成器的种子时,才意识这将成为一个真正的安全问题。哈拉姆·贝克(Hallam-Baker)表示,攻击者可以很容易地猜到种子值,并采用各种手段解密服务器的流量。 猜测种子值是一种常见的攻击,尽管它已经变得越来越复杂了。这是 2009年在 Hacker News 上的一段非常经典的攻击演练。
到1997年,计算机科学家们对生成随机数的有限选项感到厌倦,所以SGI的一个团队创建了LavaRand,这是一个网络摄像头,指向桌面上的几个熔岩灯。相机的图像数据是一个很好的熵源:就像图灵的真正随机数生成器(TRNG),并且它可以以165Kb / s的速率生成随机数据。在当时的硅谷时代,熔岩灯平台迅速获得专利。
Autodesk的创始人约翰·沃克(John Walker)意图在世界各地推广他的 HotBits,一个随机数字生成服务应用程序,由一个保证真正量子随机性的盖革计数器支持。 Random.org创建于1998,为互联网提供免费的随机数,他们现在提供的手机应用程序可以实现真正的随机抛硬币,扔骰子,扑克洗牌等。
大多数的这些发明都半途而废,但是一个叫做梅森旋转随机数生成器(The Mersenne Twister)的PRNG 软件被推广,在1997 由松本眞和西村拓士发明。它完美地平衡了性能和随机数的质量,并且经受住了时间的考验。它基于线性反馈移位寄存器(LFSR)的思想,产生一个循环周期非常长的确定性序列。近期的应用中,其循环周期可达到 2¹⁹⁹³⁷− 1。在如今的编程语言中,这种算法依旧是默认的 PRNG。
终于在1999发生了一个很大的转变。英特尔在其i810芯片组中增加了一个内置的随机数发生器。这使得新的服务器具备了来自热噪声的本地源随机数生成能力——真正的随机数生成器(TRNG)。这非常具有进步意义,但速度仍不如软件PRNGs快,所以加密软件仍然不得不依靠一个伪随机数发生器。
这节我们介绍安全加密的PRNG(CSPRNG),(这些缩写!难怪有些人认为计算机科学是枯燥的。)在SSL的时代CSPRNG非常重要。什么是CSPRNG?这里有一份 131 页的论文来介绍 CSPRNG,希望你能愉快阅读。
不言而喻,CSPRNG 具有很强的要求。梅森旋转随机数生成器并不是一种 CSPRNG,因为如果可以给定大量的先前序列样本,后面的数字可以预计出来。最近,2012年英特尔在真随机数发生器上增加了 RDRAND 和RDSEED指令,采用片上热噪声发生器可提供500MB/s的吞吐量。但RDRAND 的完整性一直被质疑。是不是存在细小的缺陷?或者是为国家安全局内置了什么东西?没有人知道这个问题的答案。我猜某些地方的某些人一定知道,可是他们也一定不会公开。
采用硬件随机数生成器 PEDOUBLER 生成的随机数。
开源硬件TRNGs于最近些年出现,其优点源自于设计的透明化:你可以检查电路本身,也可以在家里使用现成的组件建立它们。完全透明的设计不会让人怀疑这些电路优秀的随机性。REDOUBLER和无限噪声 TRNG是两个开源硬件随机数生成器,链接中给出他们的 Github 源码地址。
今天,关于随机数生产方法选择的争论仍存在于在操作系统内核,编程语言,和安全包(如 OpenSSL 或者 OpenSSH)等方面。这些算法存在多种变形用以满足不同的速度、空间和安全要求,安全专家总是在寻找新的方法来攻破已有算法的实现。但是对于日常使用,在大多数的操作系统中我们可以放心地使用 /dev/random,或者编程语言中的 rand() 函数,它们都可以快速得到一段足够长的随机数列,并且你这么做,阿兰·图灵也会很开心。
来源:https://medium.freecodecamp.com/a-brief-history-of-random-numbers-9498737f5b6c
【本文是51CTO专栏机构大数据文摘的原创译文,微信公众号“大数据文摘( id: BigDataDigest)”】