如何让Python像Julia一样快地运行

Julia 与 Python 的比较

我是否应丢弃 Python 和其他语言，使用 Julia 执行技术计算?在看到 http://julialang.org/ 上的基准测试后，人们一定会这么想。Python和其他高级语言在速度上远远有些落后。但是，我想到的***个问题有所不同：Julia 团队能否以最适合 Python 的方式编写 Python 基准测试?

我对这种跨语言比较的观点是，应该根据要执行的任务来定义基准测试，然后由语言专家编写执行这些任务的***代码。如果代码全由一个语言团队编写，则存在其他语言未得到***使用的风险。

Julia 团队有一件事做得对，那就是他们将他们使用的代码发布到了 github 上。具体地讲，Python 代码可在此处找到。

***眼看到该代码，就可以证实我所害怕的偏见。该代码是以 C 风格编写的，在数组和列表上大量使用了循环。这不是使用 Python 的***方式。

我不会责怪 Julia 团队，因为我很内疚自己也有同样的偏见。但我受到了残酷的教训：付出任何代价都要避免数组或列表上的循环，因为它们确实会拖慢 Python中的速度，请参阅《Python 不是 C》。

考虑到对 C 风格的这种偏见，一个有趣的问题(至少对我而言)是，我们能否改进这些基准测试，更好地使用 Python 及其工具?

在我给出答案之前，我想说我绝不会试图贬低 Julia。在进一步开发和改进后，Julia 无疑是一种值得关注的语言。我只是想分析 Python方面的事情。实际上，我正在以此为借口来探索各种可用于让代码更快运行的 Python 工具。

在下面的内容中，我使用 Docker 镜像在 Jupyter Notebook 中使用 Python 3.4.3，其中已安装了所有的 Python 科学工具组合。我还会通过Windows 机器上的 Python 2.7.10，使用 Anaconda 来运行代码。计时是对 Python 3.4.3 执行的。包含下面的所有基准测试的完整代码的 Notebook 可在此处(https://www.ibm.com/developerworks/community/blogs/jfp/resource/julia_python.zip)找到。

鉴于各种社交媒体上的评论，我添加了这样一句话：我没有在这里使用 Python 的替代性实现。我没有编写任何 C代码：如果您不信，可试试寻找分号。本文中使用的所有工具都是 Anaconda 或其他发行版中提供的标准的 Cython 实现。下面的所有代码都在单个 Notebook中运行。

我尝试过使用来自 github 的 Julia 微性能文件，但不能使用 Julia 0.4.2 原封不动地运行它。我必须编辑它并将 @timeit 替换为@time，它才能运行。在对它们计时之前，我还必须添加对计时函数的调用，否则编译时间也将包含在内。我使用的文件位于此处。我在用于运行 Python 的同一个机器上使用 Julia 命令行接口运行它。

计时代码

Julia 团队使用的***项基准测试是 Fibonacci 函数的一段简单编码。

def fib(n): 
 
   if n<2: 
 
       return n 
 
   return fib(n-1)+fib(n-2) 

 

此函数的值随 n 的增加而快速增加，例如：

fib(100) = 354224848179261915075 

可以注意到，Python 任意精度 (arbitrary precision) 很方便。在 C 等语言中编写相同的函数需要花一些编码工作来避免整数溢出。在 Julia中，需要使用 BigInt 类型。

所有 Julia 基准测试都与运行时间有关。这是 Julia 中使用和不使用 BigInt 的计时：

0.000080 seconds (149 allocations:10.167 KB) 
 
0.012717 seconds (262.69 k allocations:4.342 MB) 

 

在 Python Notebook 中获得运行时间的一种方式是使用神奇的 %timeit。例如，在一个新单元中键入：

%timeit fib(20) 

执行它会获得输出：

100 loops, best of 3:3.33 ms per loop 

这意味着计时器执行了以下操作：

1. 运行 fib(20) 100 次，存储总运行时间
2. 运行 fib(20) 100 次，存储总运行时间
3. 运行 fib(20) 100 次，存储总运行时间
4. 从 3 次运行中获取最小的运行时间，将它除以 100，然后输出结果，该结果就是 fib(20) 的***运行时间

这些循环的大小(100 次和 3 次)会由计时器自动调整。可能会根据被计时的代码的运行速度来更改循环大小。

Python 计时与使用了 BigInt 时的 Julia 计时相比出色得多：3 毫秒与 12 毫秒。在使用任意精度时，Python 的速度是 Julia 的 4倍。

但是，Python 比 Julia 默认的 64 位整数要慢。我们看看如何在 Python 中强制使用 64 位整数。

使用 Cython 编译

一种编译方式是使用 Cython 编译器。这个编译器是使用 Python

编写的。它可以通过以下命令安装：

pip install Cython 

如果使用 Anaconda，安装会有所不同。因为安装有点复杂，所以我编写了一篇相关的博客文章：将 Cython For Anaconda 安装在 Windows 上

安装后，我们使用神奇的 %load_ext 将 Cython 加载到 Notebook 中：

%load_ext Cython 

然后就可以在我们的 Notebook 中编译代码。我们只需要将想要编译的代码放在一个单元中，包括所需的导入语句，使用神奇的 %%cython 启动该单元：

%%cython 
 
   
 
def fib_cython(n): 
 
    if n<2: 
 
        return n 
 
    return fib_cython(n-1)+fib_cython(n-2) 

 

执行该单元会无缝地编译这段代码。我们为该函数使用一个稍微不同的名称，以反映出它是使用 Cython编译的。当然，一般不需要这么做。我们可以将之前的函数替换为相同名称的已编译函数。

对它计时会得到：

1000 loops, best of 3:1.22 ms per loop 

哇，几乎比最初的 Python 代码快 3 倍!我们现在比使用 BigInt 的 Julia 快 100 倍。

我们还可以尝试静态类型。使用关键字 cpdef 而不是 def 来声明该函数。它使我们能够使用相应的 C 类型来键入函数的参数。我们的代码变成了：

%%cython 
 
  
 
cpdef long fib_cython_type(long n): 
 
   if n<2: 
 
     return n 
 
   return fib_cython_type(n-1)+fib_cython_type(n-2) 

 

执行该单元后，对它计时会得到：

10000 loops, best of 3:36 µs per loop 

太棒了，我们现在只花费了 36 微秒，比最初的基准测试快约 100 倍!这与 Julia 所花的 80 毫秒相比更出色。

有人可能会说，静态类型违背了 Python的用途。一般来讲，我比较同意这种说法，我们稍后将查看一种在不牺牲性能的情况下避免这种情形的方法。但我并不认为这是一个问题。Fibonacci函数必须使用整数来调用。我们在静态类型中失去的是 Python 所提供的任意精度。对于 Fibonacci，使用 C 类型 long

会限制输入参数的大小，因为太大的参数会导致整数溢出。

请注意，Julia 计算也是使用 64 位整数执行的，因此将我们的静态类型版本与 Julia 的对比是公平的。

缓存计算

我们在保留 Python 任意精度的情况下能做得更好。fib 函数重复执行同一种计算许多次。例如，fib(20) 将调用 fib(19) 和fib(18)。fib(19) 将调用 fib(18) 和 fib(17)。结果 fib(18) 被调用了两次。简单分析表明，fib(17) 将被调用 3 次，fib(16) 将被调用 5 次，等等。

在 Python 3 中，我们可以使用 functools 标准库来避免这些重复的计算。

from functools import lru_cache as cache 
 
@cache(maxsize=None) 
 
def fib_cache(n): 
 
    if n<2: 
 
        return n 
 
    return fib_cache(n-1)+fib_cache(n-2) 

 

对此函数计时会得到：

1000000 loops, best of 3:910 ns per loop 

速度又增加了 40 倍，比最初的 Python 代码快约 3,600 倍!考虑到我们仅向递归函数添加了一条注释，此结果非常令人难忘。

Python 2.7 中没有提供这种自动缓存。我们需要显式地转换代码，才能避免这种情况下的重复计算。

def fib_seq(n): 
 
   if n < 2: 
 
     return n 
 
   a,b = 1,0 
 
   for i in range(n-1): 
 
     a,b = a+b,a 
 
   return a 

 

请注意，此代码使用了 Python 同时分配两个局部变量的能力。对它计时会得到：

1000000 loops, best of 3:1.77 µs per loop 

我们又快了 20 倍!让我们在使用和不使用静态类型的情况下编译我们的函数。请注意，我们使用了 cdef 关键字来键入局部变量。

%%cython 
 
  
 
def fib_seq_cython(n): 
 
   if n < 2: 
 
        return n 
 
    a,b = 1,0 
 
    for i in range(n-1): 
 
        a,b = a+b,a 
 
    return a 
 
cpdef long fib_seq_cython_type(long n): 
 
    if n < 2: 
 
        return n 
 
    cdef long a,b 
 
    a,b = 1,0 
 
    for i in range(n-1): 
 
        a,b = a+b,b 
 
    return a 

 

我们可在一个单元中对两个版本计时：

%timeit fib_seq_cython(20) 
 
%timeit fib_seq_cython_type(20) 

 

结果为：

1000000 loops, best of 3:953 ns per loop 
 
10000000 loops, best of 3:51.9 ns per loop 

 

静态类型代码现在花费的时间为 51.9 纳秒，比最初的基准测试快约 60,000(六万)倍。

如果我们想计算任意输入的 Fibonacci 数，我们应坚持使用无类型版本，该版本的运行速度快 3,500 倍。还不错，对吧?

使用 Numba 编译

让我们使用另一个名为 Numba 的工具。它是针对部分 Python 版本的一个即时

(jit) 编译器。它不是对所有 Python 版本都适用，但在适用的情况下，它会带来奇迹。

安装它可能很麻烦。推荐使用像 Anaconda 这样的 Python 发行版或一个已安装了 Numba 的 Docker 镜像。完成安装后，我们导入它的 jit 编译器：

from numba import jit 

它的使用非常简单。我们仅需要向想要编译的函数添加一点修饰。我们的代码变成了：

@jit 
 
def fib_seq_numba(n): 
 
    if n < 2: 
 
        return n 
 
    (a,b) = (1,0) 
 
    for i in range(n-1): 
 
        (a,b) = (a+b,a) 
 
    return a 

 

对它计时会得到：

1000000 loops, best of 3:225 ns per loop 

比无类型的 Cython 代码更快，比最初的 Python 代码快约 16,000 倍!

使用 Numpy

我们现在来看看第二项基准测试。它是快速排序算法的实现。Julia 团队使用了以下 Python 代码：

def qsort_kernel(a, lo, hi): 
 
    i = lo 
 
    j = hi 
 
    while i < hi: 
 
        pivot = a[(lo+hi) // 2] 
 
        while i <= j: 
 
            while a[i] < pivot: 
 
                i += 1 
 
            while a[j] > pivot: 
 
                j -= 1 
 
            if i <= j: 
 
                a[i], a[j] = a[j], a[i] 
 
                i += 1 
 
                j -= 1 
 
        if lo < j: 
 
            qsort_kernel(a, lo, j) 
 
        lo = i 
 
        j = hi 
 
    return a 

 

我将他们的基准测试代码包装在一个函数中：

import random 
 
def benchmark_qsort(): 
 
    lst = [ random.random() for i in range(1,5000) ] 
 
    qsort_kernel(lst, 0, len(lst)-1) 

 

对它计时会得到：

100 loops, best of 3:18.3 ms per loop 

上述代码与 C 代码非常相似。Cython 应该能很好地处理它。除了使用 Cython 和静态类型之外，让我们使用 Numpy

数组代替列表。在数组大小较大时，比如数千个或更多元素，Numpy 数组确实比Python 列表更快。

安装 Numpy 可能会花一些时间，推荐使用 Anaconda 或一个已安装了 Python 科学工具组合的 Docker 镜像。

在使用 Cython 时，需要将 Numpy 导入到应用了 Cython 的单元中。在使用 C 类型时，还必须使用 cimport 将它作为 C 模块导入。Numpy数组使用一种表示数组元素类型和数组维数(一维、二维等)的特殊语法来声明。

%%cython 
 
  
 
import numpy as np 
 
cimport numpy as np 
 
cpdef np.ndarray[double, ndim=1] \ 
 
qsort_kernel_cython_numpy_type(np.ndarray[double, ndim=1] a, \ 
 
long lo, \ 
 
long hi): 
 
cdef: 
 
long i, j 
 
double pivot 
 
i = lo 
 
j = hi 
 
   while i < hi: 
 
     pivot = a[(lo+hi) // 2] 
 
     while i <= j: 
 
       while a[i] < pivot: 
 
         i += 1 
 
       while a[j] > pivot: 
 
         j -= 1 
 
       if i <= j: 
 
         a[i], a[j] = a[j], a[i] 
 
         i += 1 
 
         j -= 1 
 
     if lo < j: 
 
       qsort_kernel_cython_numpy_type(a, lo, j) 
 
     lo = i 
 
     j = hi 
 
   return a 
 
  
 
cpdef benchmark_qsort_numpy_cython(): 
 
  lst = np.random.rand(5000) 
 
  qsort_kernel_cython_numpy_type(lst, 0, len(lst)-1) 

 

对 benchmark_qsort_numpy_cython() 函数计时会得到：

1000 loops, best of 3:1.32 ms per loop 

我们比最初的基准测试快了约 15 倍，但这仍然不是使用 Python 的***方法。***方法是使用 Numpy 内置的 sort()函数。它的默认行为是使用快速排序算法。对此代码计时：

def benchmark_sort_numpy(): 
 
lst = np.random.rand(5000) 
 
np.sort(lst) 

 

会得到：

1000 loops, best of 3:350 µs per loop 

我们现在比最初的基准测试快 52 倍!Julia 在该基准测试上花费了 419 微秒，因此编译的 Python 快 20%。

我知道，一些读者会说我不会进行同类比较。我不同意。请记住，我们现在的任务是使用主机语言以***的方式排序输入数组。在这种情况下，***方法是使用一个内置的函数。

剖析代码

我们现在来看看第三个示例，计算 Mandelbrodt 集。Julia 团队使用了这段 Python 代码：

def mandel(z): 
 
    maxiter = 80 
 
    c = z 
 
    for n in range(maxiter): 
 
        if abs(z) > 2: 
 
            return n 
 
        z = z*z + c 
 
     return maxiter 
 
 
def mandelperf(): 
 
    r1 = np.linspace(-2.0, 0.5, 26) 
 
    r2 = np.linspace(-1.0, 1.0, 21) 
 
    return [mandel(complex(r, i)) for r in r1 for i in r2] 
 
  
 
assert sum(mandelperf()) == 14791 

 

***一行是一次合理性检查。对 mandelperf() 函数计时会得到：

100 loops, best of 3:4.62 ms per loop 

使用 Cython 会得到：

100 loops, best of 3:1.94 ms per loop 

还不错，但我们可以使用 Numba 做得更好。不幸的是，Numba 还不会编译列表推导式 (list

comprehension)。因此，我们不能将它应用到第二个函数，但我们可以将它应用到***个函数。我们的代码类似以下代码。

@jit 
 
def mandel_numba(z): 
 
    maxiter = 80 
 
    c = z 
 
    for n in range(maxiter): 
 
        if abs(z) > 2: 
 
            return n 
 
        z = z*z + c 
 
     return maxiter 
 
def mandelperf_numba(): 
 
    r1 = np.linspace(-2.0, 0.5, 26) 
 
    r2 = np.linspace(-1.0, 1.0, 21) 
 
    return [mandel_numba(complex(r, i)) for r in r1 for i in r2] 

 

对它计时会得到：

1000 loops, best of 3:503 µs per loop 

还不错，比 Cython 快 4 倍，比最初的 Python 代码快 9 倍!

我们还能做得更好吗?要知道是否能做得更好，一种方式是剖析代码。内置的 %prun 剖析器在这里不够精确，我们必须使用一个称为 line_profiler 的更好的剖析器。它可以通过pip 进行安装：

pip install line_profiler 

安装后，我们需要加载它：

%load_ext line_profiler 

然后使用一个神奇的命令剖析该函数：

%lprun -s -f mandelperf_numba mandelperf_numba() 

它在一个弹出窗口中输出以下信息。

Timer unit:1e-06 s 
 
Total time:0.003666 s 
 
File: 
 
Function: mandelperf_numba at line 11 
 
Line # Hits Time Per Hit % Time Line Contents 
 
============================================================== 
 
11 def mandelperf_numba(): 
 
12 1 1994 1994.0 54.4 r1 = np.linspace(-2.0, 0.5, 26) 
 
13 1 267 267.0 7.3 r2 = np.linspace(-1.0, 1.0, 21) 
 
14 1 1405 1405.0 38.3 return [mandel_numba(complex(r, i)) for r in r1 for i in r2] 

 

我们看到，大部分时间都花费在了 mandelperf_numba() 函数的***行和***一行上。***一行有点复杂，让我们将它分为两部分来再次剖析：

def mandelperf_numba(): 
 
    r1 = np.linspace(-2.0, 0.5, 26) 
 
    r2 = np.linspace(-1.0, 1.0, 21) 
 
    c3 = [complex(r, i) for r in r1 for i in r2] 
 
    return [mandel_numba(c) for c in c3] 

 

剖析器输出变成：

Timer unit:1e-06 s 
 
Total time:0.002002 s 
 
File: 
 
Function: mandelperf_numba at line 11 
 
Line # Hits Time Per Hit % Time Line Contents 
 
============================================================== 
 
11 def mandelperf_numba(): 
 
12 1 678 678.0 33.9 r1 = np.linspace(-2.0, 0.5, 26) 
 
13 1 235 235.0 11.7 r2 = np.linspace(-1.0, 1.0, 21) 
 
14 1 617 617.0 30.8 c3 = [complex(r, i) for r in r1 for i in r2] 
 
15 1 472 472.0 23.6 return [mandel_numba(c) for c in c3] 

 

我们可以看到，对函数 mandel_numba() 的调用仅花费了总时间的 1/4。剩余时间花在 mandelperf_numba()

函数上。花时间优化它是值得的。

再次使用 Numpy

使用 Cython 在这里没有太大帮助，而且 Numba 不适用。摆脱此困境的一种方法是再次使用 Numpy。我们将以下代码替换为生成等效结果的 Numpy

代码。

return [mandel_numba(complex(r, i)) for r in r1 for i in r2] 

此代码构建了所谓的二维网格。它计算由 r1 和 r2 提供坐标的点的复数表示。点 Pij 的坐标为 r1[i] 和 r2[j]。Pij 通过复数 r1[i] +

1j*r2[j] 进行表示，其中特殊常量 1j 表示单个虚数 i。

我们可以直接编写此计算的代码：

 

@jit 
 
def mandelperf_numba_mesh(): 
 
    width = 26 
 
    height = 21 
 
    r1 = np.linspace(-2.0, 0.5, width) 
 
    r2 = np.linspace(-1.0, 1.0, height) 
 
    mandel_set = np.zeros((width,height), dtype=int) 
 
    for i in range(width): 
 
        for j in range(height): 
 
            mandel_set[i,j] = mandel_numba(r1[i] + 1j*r2[j]) 
 
     return mandel_set 

 

请注意，我将返回值更改为了一个二维整数数组。如果要显示结果，该结果与我们需要的结果更接近。

对它计时会得到：

10000 loops, best of 3:140 µs per loop 

我们比最初的 Python 代码快约 33 倍!Julia 在该基准测试上花费了 196 微秒，因此编译的 Python 快 40%。

向量化

让我们来看另一个示例。老实地讲，我不确定要度量什么，但这是 Julia 团队使用的代码。

def parse_int(t): 
 
    for i in range(1,t): 
 
        n = random.randint(0,2**32-1) 
 
        s = hex(n) 
 
        if s[-1]=='L': 
 
            s = s[0:-1] 
 
        m = int(s,16) 
 
        assert m == n 
 
    return n 

 

实际上，Julia 团队的代码有一条额外的指令，用于在存在末尾的 ‘L’ 时删除它。我的 Anaconda 安装需要这一行，但我的 Python 3安装不需要它，所以我删除了它。最初的代码是：

def parse_int(t): 
 
    for i in range(1,t): 
 
        n = random.randint(0,2**32-1) 
 
        s = hex(n) 
 
        if s[-1]=='L': 
 
            s = s[0:-1] 
 
        m = int(s,16) 
 
        assert m == n 
 
    return n 

 

对修改后的代码计时会得到：

100 loops, best of 3:3.33 ms per loop 

Numba 似乎没什么帮助。Cython 代码运行速度快了约 5 倍：

1000 loops, best of 3:617 µs per loop 

Cython 代码运行速度快了约 5 倍，但这还不足以弥补与 Julia 的差距。

我对此基准测试感到迷惑不解，我剖析了最初的代码。以下是结果：

Timer unit:1e-06 s 
 
Total time:0.013807 s 
 
File: 
 
Function: parse_int at line 1 
 
Line # Hits Time Per Hit % Time Line Contents 
 
============================================================== 
 
1 def parse_int(): 
 
2 1000 699 0.7 5.1 for i in range(1,1000): 
 
3 999 9149 9.2 66.3 n = random.randint(0,2**32-1) 
 
4 999 1024 1.0 7.4 s = hex(n) 
 
5 999 863 0.9 6.3 if s[-1]=='L': 
 
6 s = s[0:-1] 
 
7 999 1334 1.3 9.7 m = int(s,16) 
 
8 999 738 0.7 5.3 assert m == n 

 

可以看到，大部分时间都花费在了生成随机数上。我不确定这是不是该基准测试的意图。

加速此测试的一种方式是使用 Numpy 将随机数生成移到循环之外。我们一次性创建一个随机数数组。

def parse_int_vec(): 
 
    n = np.random.randint(0,2**32-1,1000) 
 
        for i in range(1,1000): 
 
            ni = n[i] 
 
            s = hex(ni) 
 
        m = int(s,16) 
 
        assert m == ni 

 

对它计时会得到：

1000 loops, best of 3:848 µs per loop 

还不错，快了 4 倍，接近于 Cython 代码的速度。

拥有数组后，通过循环它来一次向某个元素应用 hex() 和 int() 函数似乎很傻。好消息是，Numpy 提供了一种向数组应用函数的方法，而不必使用循环，该函数是numpy.vectorize() 函数。此函数接受一次处理一个对象的函数。它返回一个处理数组的新函数。

vhex = np.vectorize(hex) 
 
vint = np.vectorize(int) 
 
def parse_int_numpy(): 
 
    n = np.random.randint(0,2**32-1,1000) 
 
    s = vhex(n) 
 
    m = vint(s,16) 
 
    np.all(m == n) 
 
    return s 

 

此代码运行速度更快了一点，几乎像 Cython 代码一样快：

1000 loops, best of 3:703 µs per loop 

我肯定 Python 专家能够比我在这里做得更好，因为我不太熟悉 Python 解析，但这再一次表明避免 Python 循环是个不错的想法。

结束语

上面介绍了如何加快 Julia 团队所使用的 4 个示例的运行速度。还有 3 个例子：

• pisum 使用 Numba 的运行速度快 29 倍。
• randmatstat 使用 Numpy 可将速度提高 2 倍。
• randmatmul 很简单，没有工具可应用到它之上。

包含所有 7 个示例的完整代码的 Notebook 可在此处获得。

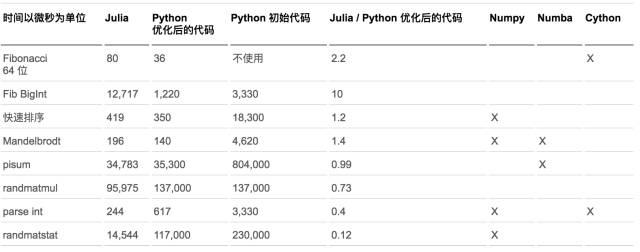
我们在一个表格中总结一下我们的结果。我们给出了在最初的 Python 代码与优化的代码之间实现的加速。我们还给出了对 Julia 团队使用的每个基准测试示例使用的工具。

 

 

这个表格表明，在前 4 个示例中，优化的 Python 代码比 Julia 更快，后 3 个示例更慢。请注意，为了公平起见，对于 Fibonacci，我使用了递归代码。

我认为这些小型的基准测试没有提供哪种语言最快的明确答案。举例而言， randmatstat 示例处理 5×5 矩阵。使用 Numpy 数组处理它有点小题大做。应该使用更大的矩阵执行基准测试。

我相信，应该在更复杂的代码上对语言执行基准测试。Python 与 Julia 比较–一个来自机器学习的示例中提供了一个不错的示例。在该文章中，Julia 似乎优于 Cython。如果我有时间，我会使用 Numba试一下。

无论如何，可以说，在这个小型基准测试上，使用正确的工具时，Python 的性能与 Julia 的性能不相上下。相反地，我们也可以说，Julia 的性能与编译后的

Python 不相上下。考虑到 Julia 不需要对代码进行任何注释或修改，所以这本身就很有趣。

补充说明

我们暂停一会儿。我们已经看到在 Python 代码性能至关重要时，应该使用许多工具：

• 使用 line_profiler 执行剖析。
• 编写更好的 Python 代码来避免不必要的计算。
• 使用向量化的操作和通过 Numpy 来广播。
• 使用 Cython 或 Numba 编译。

使用这些工具来了解它们在哪些地方很有用。与此同时，请谨慎使用这些工具。分析您的代码，以便可以将精力放在值得优化的地方。重写代码来让它变得更快，有时会让它难以理解或通用性降低。因此，仅在得到的加速物有所值时这么做。Donald Knuth 曾经恰如其分地提出了这条建议：

“我们在 97% 的时间应该忘记较小的效率：不成熟的优化是万恶之源。”

但是请注意，Knuth 的引语并不意味着优化是不值得的，例如，请查看停止错误地引用 Donald Knuth 的话!和‘不成熟的优化是恶魔’的谎言。

Python 代码可以优化，而且应该在有意义的时间和位置进行优化。