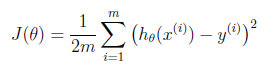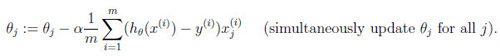在梯度下降算法理论篇中,曾经感叹推导过程如此苍白,如此期待仿真来给我更加直观的感觉。当我昨晚Octave仿真后,那种成就感着实难以抑制。分享一下仿真的过程和结果,并且将上篇中未理解透澈的内容补上。
在Gradient Descent Algorithm中,我们利用不断推导得到两个对此算法非常重要的公式,一个是J(θ)的求解公式,另一个是θ的求解公式:
我们在仿真中,直接使用这两个公式,来绘制J(θ)的分布曲面,以及θ的求解路径。
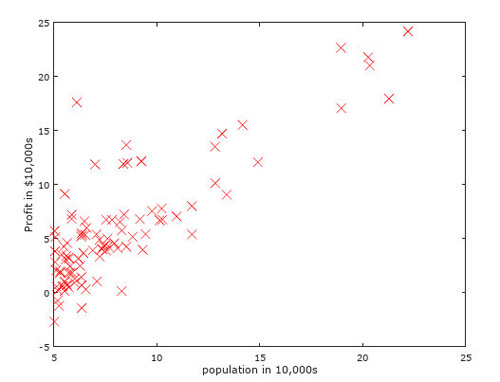
命题为:我们为一家连锁餐饮企业新店开张的选址进行利润估算,手中掌握了该连锁集团所辖店铺当地人口数据,及利润金额,需要使用线性回归算法来建立人口与利润的关系,进而为新店进行利润估算,以评估店铺运营前景。
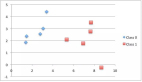
首先我们将该企业的数据绘制在坐标图上,如下图所示,我们需要建立的模型是一条直线,能够在最佳程度上,拟合population与profit之间的关系。其模型为:
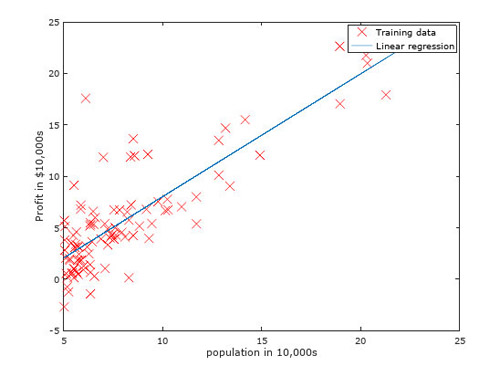
在逼近θ的过程中,我们如下实现梯度下降:进行了1500次的迭代(相当于朝着最佳拟合点行走1500步),我们在1500步后,得到θ=[-3.630291,1.166362];在3000次迭代后,其值为[-3.878051,1.191253];而如果运行10万次,其值为[-3.895781,1.193034]。可见,最初的步子走的是非常大的,而后,由于距离最佳拟合点越来越近,梯度越来越小,所以步子也会越来越小。为了节约运算时间,1500步是一个完全够用的迭代次数。之后,我们绘制出拟合好的曲线,可以看得出,拟合程度还是不错的。
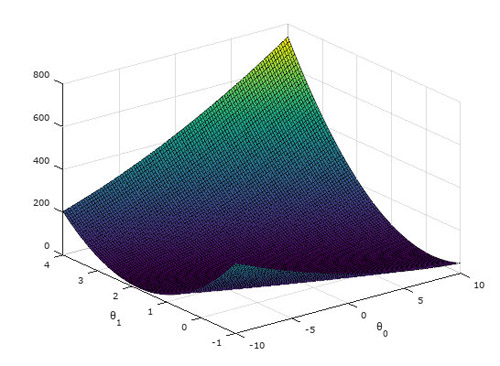
下图是J(θ)的分布曲面:
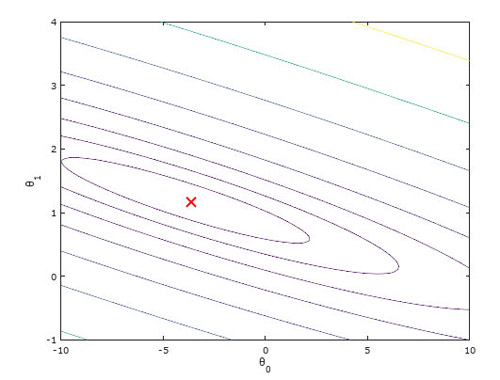
接来下是我们求得的最佳θ值在等高线图上所在的位置,和上一张图其实可以重合在一起:
关键代码如下:
1、计算j(theta)
- function J = computeCost(X, y, theta)
- %COMPUTECOST Compute cost for linear regression
- % J = COMPUTECOST(X, y, theta) computes the cost of using theta as the
- % parameter for linear regression to fit the data points in X and y
- % Initialize some useful values
- m = length(y); % number of training examples
- % You need to return the following variables correctly
- J = 0;
- % ====================== YOUR CODE HERE ======================
- % Instructions: Compute the cost of a particular choice of theta
- % You should set J to the cost.
- h = X*theta;
- e = h-y;
- J = e'*e/(2*m)
- % =========================================================================
- end
2、梯度下降算法:
- function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
- %GRADIENTDESCENT Performs gradient descent to learn theta
- % theta = GRADIENTDESENT(X, y, theta, alpha, num_iters) updates theta by
- % taking num_iters gradient steps with learning rate alpha
- % Initialize some useful values
- m = length(y); % number of training examples
- J_history = zeros(num_iters, 1);
- for iter = 1:num_iters
- % ====================== YOUR CODE HERE ======================
- % Instructions: Perform a single gradient step on the parameter vector
- % theta.
- %
- % Hint: While debugging, it can be useful to print out the values
- % of the cost function (computeCost) and gradient here.
- %
- h=X*theta;
- e=h-y;
- theta = theta-alpha*(X'*e)/m;
- % ============================================================
- % Save the cost J in every iteration
- J_history(iter) = computeCost(X, y, theta);
- end
- end