生活中的所有事物都是与时间相关的,也就形成了一个序列。为了对序列数据(文本、演讲、视频等)我们可以使用神经网络并导入整个序列,但是这样我们的数据输入尺寸是固定的,局限性就很明显。如果重要的时序特征事件恰好落在输入窗以外,就会产生更大的问题。所以我们需要的是:
-
能对任意长度序列做逐个元素读取的神经网络(比如视频就是一系列的图片;我们每次给神经网络一张图);
-
有记忆的神经网络,能够记得若干个时间步以前的事件、这些问题和需求已经催生出多中不同的循环神经网络。
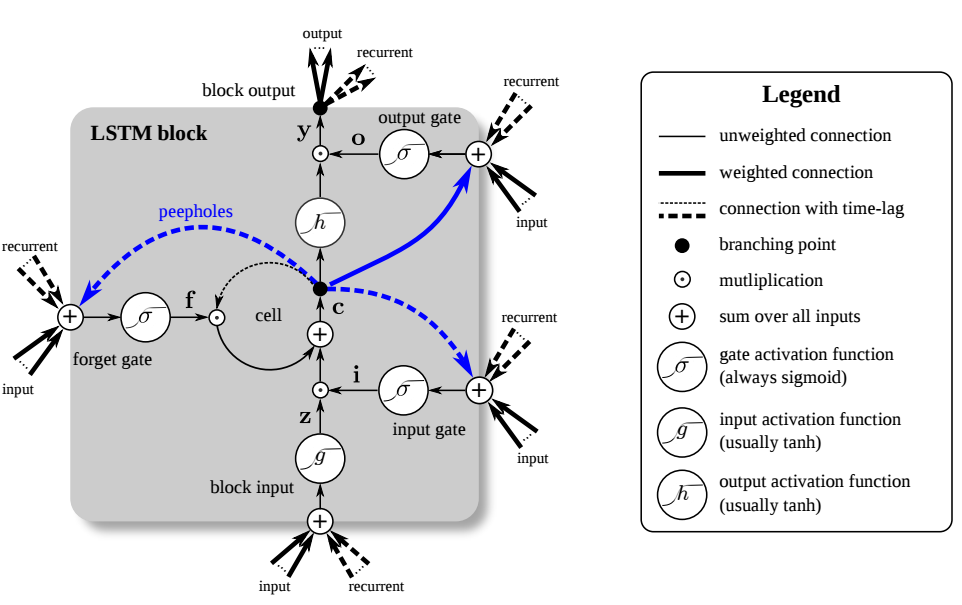
图1:长短期记忆(LSTM)单元。LSTM有四个输入权重和四个循环权重。Peepholes是记忆细胞和门之间的额外连接,但他们对性能提升帮助不到,所以常被忽略。
循环神经网络
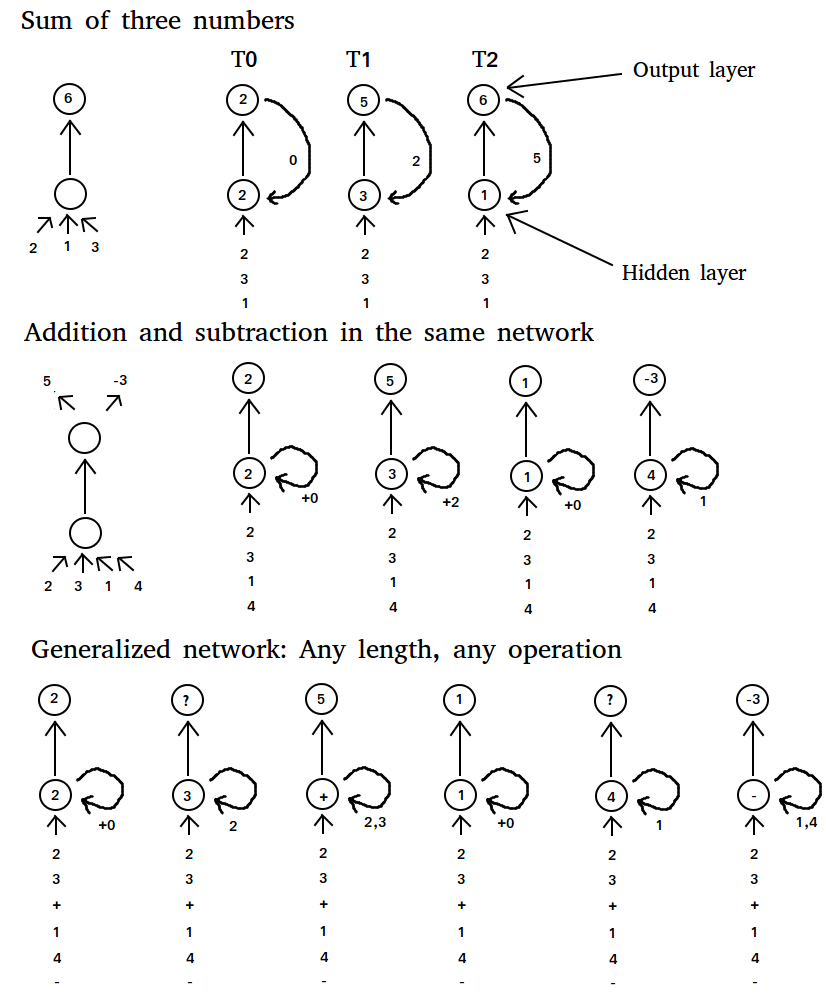
若我们想让一个常规的神经网络解决两个数相加的问题,那我们只需要输入两个数字,再训练两数之和的预测即可。如果现在有3个数要相加,那么我们可以:
-
拓展网络架构,添加输入和权重,再重新训练;
-
把第一次的输出(即两数之和)和第三个数作为输入,再返回给网络。
方案(2)显然更好,因为我们希望避免重新训练整个网络(网络已经“知道”如何将两个数相加)。如果我们的任务变成:先对两数做加法,再减去两个不同的数,那这个方案又不好使了。即使我们使用额外的权重,也不能保证正确的输出。相反,我们可以尝试“修改程序”,把网络由“加法”变成“减法”。通过隐藏层的加权可以实现这一步(见图2),如此便让网络的内核随着每个新的输入而变化。网络将学习着在相加两个数之后,把程序从“加法”变成“减法”,然后就解决了问题。
我们甚至可以泛化这一方法,传递给网络两个数字,再传入一个“特殊”的数字——代表着数学运算“加法”,“减法”或“乘法”。实践当中这样或许不尽完美,但也能得到大体正确的结果了。不过这里的主要问题倒不在于得到正确结果,而是我们可以训练循环神经网络,使之能够学习任意输入序列所产生的特殊输出,这就威力大了。
例如,我们可以教网络学会词语的序列。Soumith Chintala和Wojciech Zaremba写了一篇优秀的博客讲述用RNN做自然语言处理。RNN也可以用于生成序列。Andrej Karpathy写了这篇[有趣而生动的博客],展示了字词级别的RNN,可以模仿各种文风,从莎士比亚,到Linux源码,再到给小孩儿起名。
长短期记忆(Long Short Term Memory, LSTM)
长短期记忆单元使用自连接的线性单元,权重为常数1.0。这使得流入自循环的值(前向传播)或梯度(反向传播)可以保持不变(乘以1.0的输入或误差还是原来的值;前一时间步的输出或误差也和下一时间步的输出相同),因而所有的值和梯度都可以在需要的时候准确回调。这个自循环的单元,记忆细胞,提供了一种可以储存信息的记忆功能,对之前的若干个时间步当中有效。这对很多任务都极其有效,比如文本数据,LSTM可以存储前一段的信息,并对当前段落的序列应用这些信息。
另外,深度网络中一个很普遍的问题叫作“梯度消失”问题,也即,梯度随着层数增多而越来越小。有了LSTM中的记忆细胞,就有了连续的梯度流(误差保持原值),从而消除了梯度消失问题,能够学习几百个时间步那么长的序列。
然而有时我们会想要抛掉旧有信息,替换以更新、更相关的信息。同时我们又不想释放无效信息干扰其余部分的网络。为了解决这个问题,LSTM单元拥有一个遗忘门,在不对网络释放信息的情况下删除自循环单元内的信息(见图1)。遗忘门将记忆细胞里的值乘以0~1之间的数字,其中0表示遗忘,1表示保持原样。具体的数值宥当前输入和上一时间步的LSTM单元输出决定。
在其他时间,记忆细胞还需要保持多个时间步内不变,为此LSTM增加了另一道门,输入门(或写入门)。当输入门关闭时,新信息就不会流入,原有信息得到保护。
另一个门将记忆细胞的输出值乘以0(抹除输出)~1()之间的数,当多个记忆相互竞争时这很有用:一个记忆细胞可能说:“我的记忆非常重要!所以我现在就要释放”,但是网络却可能说:“你的记忆是很重要,不过现在又其他更重要的记忆细胞,所以我给你的输出门赋予一个微小的数值,给其他门大数值,这样他们会胜出”。
LSTM单元的连接方式初看可能有些复杂,你需要一些时间去理解。但是当你分别考察各个部件的时候,会发现其结构其实跟普通的循环神经网络没啥两样——输入和循环权重流向所有的门,连接到自循环记忆细胞。
想要更深入地了解LSTM并认识整个架构,我推荐阅读:LSTM: A Search Space Odyssey和original LSTM paper。
词嵌入(Word Embedding)
图3:菜谱的二维词嵌入空间,这里我们局部放大了“南欧”的聚类群
想象"cat"和其他所有与"cat"相关联的词汇,你可能会想到"kitten","feline"。再想一些不那么相似,但是又比"car"要相似得多的,比如"lion","tiger","dog","animal"或者动词"purring","mewing","sleeping"等等。
再想象一个三维的空间,我们把词"cat"放在正中间。上面提到的词语当中,与"cat"相似的,空间位置也离得更近;比如"kitty","feline"就离中央很近;"tiger"和"lion"就稍微远一点;"dog"再远一点;而"car"就不知远到哪里去了。可以看图3这个词嵌入二维空间的例子。
如果我们我们用向量来代表空间里的每一个词,那么每个向量就由3个坐标构成,比如"cat"是(0, 0, 0),"kitty"可能是(0,1, 0,2, -0,3)而"car"则是(10, 0, -15)。这个向量空间,就是词嵌入空间,每个词对应的三个坐标可以用做算法的输入数据。
典型的词嵌入空间含有上千个词和上百个维度,人类是很难直观理解的,但是相似的词距离近这个规律仍然成立。对于机器来说,这是一种很好的词汇表征,可以提高自然语言处理能力。
如果你想要学习更多词嵌入的内容,以及如何应用于创建模型“理解”语言,推荐阅读:Understanding Natural Language with Deep Neural Networks Using Torch,作者:Soumith Chintala和Wojciech Zaremba。
编码-解码
让我们暂时停下自然语言处理,来想象一个西红柿,想象那些适合西红柿的配料或菜肴。如果你的想法和那些网上最常见的菜谱差不多,那你想到的可能是诸如奶酪和萨拉米;帕尔马干酪、罗勒、通心粉;或其他配料比如橄榄油、百里香和西芹等等。(换作中国人来想,肯定是鸡蛋)。这些配料主要都是意大利、地中海菜系。
还是那个西红柿,如果要吃墨西哥菜系,你想到的可能是豆子、玉米、辣椒、芫荽叶或鳄梨。
你刚才所想的,就是把词汇“西红柿”的表征变换成了新的表征:“墨西哥菜里的西红柿”。
“编码”(Encoder)做的是同样的事,它通过变换词汇的表征,把输入词汇逐个变换为新的“思维向量”。就像给“西红柿”加入了上下文“墨西哥菜”,这是“编码-解码”架构的第一步。
编码-解码架构的第二步是基于这样一个事实:不同的语种在词嵌入空间里,具有相似的几何结构,即便对同一个事物,描述用词完全不同。比如在德语里“猫”是"Katze",狗是"Hund",与英语截然不同,但是两个词之间的关系确实一样。Karze与Hund的关系,跟Car与Dog的关系完全一致,换言之,即使词汇本身不同,他们背后的“思维向量”确实一样的。当然也有些词汇很难用其他语言表达(比如中文里的“缘分”之类),但是这种情况比较稀罕,总体上是成立的。
基于以上思想,我们就可以构建解码网络了。我们把英语编码器产生的“思维向量”传递给德语解码器。德语解码器会把这些思维向量或关系变换映射到德语词嵌入空间里,然后就会产生一句话,保持英语句子里的关系。如此我们就有了一个能做翻译的网络,这个思想目前仍在发展,结果虽然不完美,但却在极快提高,不久就会成为翻译的最佳方法。