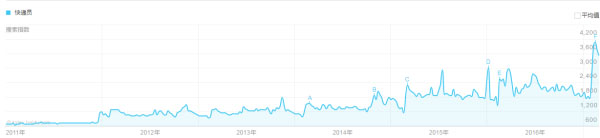
在这个购物和吃饭都可足不出户的时代,快递员应该是大部分人接触最多的第二职业,第一职业当然是自己的职业(从下图快递员的搜索趋势增长就可见一斑)。快递员也成为我们最可爱的人,除了爸爸妈妈之外,最关心我们衣食住行。
对不少都市白领而言,几乎每天坐电梯去办公室都会遇到快递员背着无数包裹逐层送快递。发现大部分快递员都是采用如下流程:坐电梯直接去到收件人群中的最高楼层,然后从高到底逐层往下送达;或者反之,从低到高逐层投递,然后从最高的目标层下来。
然而这是最优算法吗,这是闲得蛋疼的作者在本文需要重点讨论的问题。
显然,快递员对某写字楼所有快递送货的时间(T)是需要优化的目标。T=快递员乘坐电梯的总运行时间(T1)+快递员乘坐电梯的总停靠时间(T2)+快递员在各楼层等待电梯的总时间(T3)+快递员在每层送货的总时间(T4)。
- T1,快递员乘坐的电梯在竖井内运动所花费的时间,不含电梯在静止状态下的开门关门及上下乘客所花费的时间。其最小值是从底层起始楼层到目的地最高楼层然后回到底层的时间。所以最小化只要不走重复路线就可以搞定。(不考虑电梯停靠而需要减速和加速对速度的影响)
- T2,这主要是快递员从A层到B层时,中间有人上下电梯引起的停靠时间(包括:电梯开关门以及乘客上下的时间)。
- T3,在完成每层的送货之后,需要在该层等待电梯上楼或者下楼去下一个目标楼层。影响该时间的输入变量极多,不在本次讨论范围之内。
- T4,快递员在每层需要按收件人挨个送货。其耗时总和与乘坐电梯的策略无关,也不在本次讨论范围之内。
经过模型简化,快递员要优化时间T,核心是优化T1和T2。如上所述,T1的最优化比较简单直接,只要不走重复路线或者回头路,即可最优化。T2是本次的优化重点。T2主要是因为,在快递员去往下一个楼层的时候,中途有人上电梯或下电梯导致。而其他人上电梯是完全隐性的,只有同行人(与快递员同时乘坐电梯的人)下电梯的目标楼层才是显性的,可以通过查看电梯内的楼层面板得到信息。本次优化的要点也是通过考虑同行人的目标楼层,动态调整快递员自己的下一个目标楼层使得T2最小,而不是坚持固定的行程。
优化算法也很简单,如下:
- 将行程分为两段:L1(从最初的起始层开始,停靠0次或数次,到达目的地最高层)和L2(从目的地最高层,停靠0次或数次,回到最初的起始层)
- 在L1的去程中,快递员的下一个目标楼层,应使得从本层去下一个目标楼层之间有最少的同行人目标楼层(即停靠次数最小)。如存在多个目标楼层满足上述条件,取其中的最大值。
- 在L2的回程中,快递员从高到低,逐层停靠尚未送货的楼层完成任务,直到回到最初的起始层。
- 无论在L1还是L2中,如果有他人上电梯且该层为快递员需要送货且没有完成任务的楼层,立即下电梯完成送货任务。
以上论述比较绕口,其实核心就两条:
- 尽量减少中间有人下电梯增加停靠时间。特别是从下往上的过程中,中途上电梯的概率较低而中途下电梯的概率高,重点要使用策略保证不让要下电梯的同行人在自己前面而增加停靠次数。
- 尽量保持机会(option),当遇到有人上电梯时可以顺势下电梯完成送货任务来减少停靠时间。特别是从上往下的过程中,中途下电梯的概率低而中途上电梯的概率高,重点要保留下电梯的机会与上电梯的人同层,可以顺势下电梯完成任务从而避免停靠。
举例来说明:
- 快递员从1层出发,需要去到3、4、7、9和10层送货,在1楼上电梯的同行人按下了5层。
- 这时候快递员的策略是按下4层,先去4层送货。(避免了5层的停靠,此时3层和4层都满足该优化,但因为4>3,所以先去4层)
- 4层送货完成后,接着坐电梯去更高楼层送货。上电梯之后,发现里面的同行人要去8层,那就按下7层并去该楼层完成送货。(避免了8层的停靠)
- 7层送货完成后,接着坐电梯去更高楼层送货,此时电梯内没有同行人,这时按下10层按钮网上。在9层时,电梯打开有人要上电梯往上,这时顺势在9层下电梯完成送货。(避免了9层的停靠)
- 9层送货完成后,接着坐电梯去10层送货。完成后,从10层坐电梯下到3层完成送货,并最后回到1层。
当然本次讨论忽略了许多细节,比如如何减少每次等待电梯的时间等等。而往往等待电梯是最费时间的,但是从现有的信息来看,等待时间是各种参数影响而比较随机,因此无法在模型中考虑而优化。
【本文为51CTO专栏作者“数据冰山”的原创稿件,转载请通过作者微信公众号(shujubingshan)获取联系】